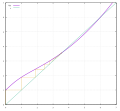
Fixed-point computation refers to the process of computing an exact or approximate fixed point of a given function. In its most common form, the given...

contrasted to the more complicated and computationally demanding floating-point representation. In the fixed-point representation, the fraction is often...

In mathematics, a fixed point (sometimes shortened to fixpoint), also known as an invariant point, is a value that does not change under a given transformation...

In combinatory logic for computer science, a fixed-point combinator (or fixpoint combinator): p.26  is a higher-order function (i.e., a function which...

Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after L. E. J. (Bertus) Brouwer. It states that for any continuous function f...

was actually introduced by a fixed-point computation, but the underlying issue would have been the same with floating-point arithmetic. Salami slicing is...

the number of queries is given. List of root finding algorithms Fixed-point computation Broyden's method – Quasi-Newton root-finding method for the multivariable...

In mathematics, the Banach fixed-point theorem (also known as the contraction mapping theorem or contractive mapping theorem or Banach–Caccioppoli theorem)...

In numerical analysis, fixed-point iteration is a method of computing fixed points of a function. More specifically, given a function f {\displaystyle...

In mathematical logic, fixed-point logics are extensions of classical predicate logic that have been introduced to express recursion. Their development...

search. On the other hand, determining whether a given fixed point is unique is computationally hard: For d=2, for componentwise lattice and a value-oracle...

point operations per second (FLOPS, flops or flop/s) is a measure of computer performance in computing, useful in fields of scientific computations that...

that can compute with exact real numbers instead of the binary fixed-point or floating-point numbers used by most actual computers. The real RAM was formulated...

Floating-point error mitigation is the minimization of errors caused by the fact that real numbers cannot, in general, be accurately represented in a fixed space...

mathematics, the theory of computation is the branch that deals with what problems can be solved on a model of computation, using an algorithm, how efficiently...

{\displaystyle f} is computationally expensive. Anderson acceleration is a method to accelerate the convergence of the fixed-point sequence. Define the...

representation of a number is fixed (fixed-point, floating-point and interval arithmetic), the main concern is to control the computational error, as far as possible;...

theory, the Kleene fixed-point theorem, named after American mathematician Stephen Cole Kleene, states the following: Kleene Fixed-Point Theorem. Suppose...

In computational geometry, the point-in-polygon (PIP) problem asks whether a given point in the plane lies inside, outside, or on the boundary of a polygon...

converge to Ω as n approaches infinity. This is because Ω is an attractive fixed point of the function e−x. It is much more efficient to use the iteration Ω...

fixed-point free. The fixed-point theorem shows that no total computable function is fixed-point free, but there are many non-computable fixed-point-free...

which object a query ray intersects first. If the search space is fixed, the computational complexity for this class of problems is usually estimated by:...

The International Fixed Calendar (also known as the Cotsworth plan, the Cotsworth calendar, the Eastman plan or the Yearal) was a proposed reform of the...

invariance of domain. Sperner colorings have been used for effective computation of fixed points and in root-finding algorithms, and are applied in fair division...

Secure multi-party computation (also known as secure computation, multi-party computation (MPC) or privacy-preserving computation) is a subfield of cryptography...

Scarf's fixed-point method was a break-through in the mathematics of computation generally, and specifically in optimization and computational economics...

available for arbitrary-precision integer and floating-point math. Rather than storing values as a fixed number of bits related to the size of the processor...

and adding 1). However, while the number of binary bits is fixed throughout a computation it is otherwise arbitrary. Unlike the ones' complement scheme...

Asano, Jiří Matoušek, and Takeshi Tokuyama in 2007. Formally, it is a fixed point of a certain function. Its existence or uniqueness are not clear in advance...

process applied to fixed-point iteration. Viewed in this way, Steffensen's method naturally generalizes to efficient fixed-point calculation in general...