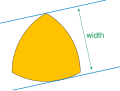
In geometry, the four-vertex theorem states that the curvature along a simple, closed, smooth plane curve has at least four local extrema (specifically...

In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map...

inflection points. The theorem is analogous to the four-vertex theorem according to which any smooth closed plane curve has at least four points of extreme...

known for the first proof of the four-vertex theorem that applied in general to non-convex curves. Kneser's theorem on differential equations is named...

Agoston (2005), Theorem 9.3.9, p. 570; Gibson (2001), Section 9.3, "The Four Vertex Theorem", pp. 133–136; Fuchs & Tabachnikov (2007), Theorem 10.3, p. 149...

(by the four-vertex theorem, there are at least four vertices where the curvature reaches an extreme point) but for such curves the theorem can be applied...

Retrieved 2019-11-27. Shonkwiler, Clay (October 6, 2006). "The Four Vertex Theorem and its Converse" (PDF). math.colostate.edu. Retrieved 2019-11-26...

(symplectic topology) Euler's theorem (differential geometry) Four-vertex theorem (differential geometry) Frobenius theorem (foliations) Gauss's lemma (riemannian...

oval has four turns, a tri-oval has six. More formally, according to the four-vertex theorem, every smooth simple closed curve has at least four vertices...

1937) was an Indian mathematician who introduced the four-vertex theorem and Mukhopadhyaya's theorem in plane geometry. Syamadas Mukhopadhyaya was born...

Firstly, any given vertex will be the middle of either 0 × 5 = 0 (all edges from the vertex are the same colour), 1 × 4 = 4 (four are the same colour...

Kawasaki's theorem or Kawasaki–Justin theorem is a theorem in the mathematics of paper folding that describes the crease patterns with a single vertex that...

color theorem based on Kempe's work. First of all, one associates a simple planar graph G {\displaystyle G} to the given map, namely one puts a vertex in...

curvature. All closed curves will have at least four vertices, two minima and two maxima (the four-vertex theorem). In general a curve will not have 4th-order...

Erdős–Pósa theorem, named after Paul Erdős and Lajos Pósa, relates two parameters of a graph: The size of the largest collection of vertex-disjoint cycles...

is fixed. The theorem suggests that when this depth is at the value creating a right vertex, the generalization of Pythagoras' theorem applies. In a different...

In mathematics, the Erdős–Ko–Rado theorem limits the number of sets in a family of sets for which every two sets have at least one element in common....

and topological generalization of the classical four-vertex theorem, that a plane curve has at least four extrema of curvature, specifically, at least two...

The theorem is helpful for solving competitive Euclidean geometry problems, and can be used to reconstruct a triangle starting from one vertex, the incenter...

another vertex adjacent to an odd number of triangle vertices). However, the algorithm of Degiorgi & Simon (1995) uses only Whitney's isomorphism theorem. It...

stands in contrast to the four-vertex theorem, according to which every simple closed smooth curve in the plane has at least four vertices. Some curves,...

computer) in ISI Syamadas Mukhopadhyaya, introduced the four-vertex theorem and Mukhopadhyaya's theorem in eucliden geometry ANM Muniruzzaman, Bangladeshi...

inscribed circle touches each side. This divides the four sides into eight segments, between a vertex of the quadrilateral and a point of tangency with the...

In graph theory, the Robertson–Seymour theorem (also called the graph minors theorem) states that the undirected graphs, partially ordered by the graph...

by the Tutte theorem G contains a perfect matching. Let Gi be a component with an odd number of vertices in the graph induced by the vertex set V − U. Let...

Alexandrov's theorem on polyhedra is a rigidity theorem in mathematics, describing three-dimensional convex polyhedra in terms of the distances between...

In graph theory, Wagner's theorem is a mathematical forbidden graph characterization of planar graphs, named after Klaus Wagner, stating that a finite...

is monostatic. This was shown by V. Arnold via reduction to the four-vertex theorem. There are no monostatic simplices in dimension up to eight. In dimension...

valid guard set, because every triangle of the polygon is guarded by its vertex with that color. Since the three colors partition the n vertices of the...

In geometry, Pick's theorem provides a formula for the area of a simple polygon with integer vertex coordinates, in terms of the number of integer points...