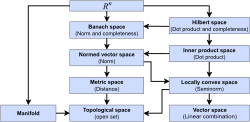
In mathematics, a topological vector space (also called a linear topological space and commonly abbreviated TVS or t.v.s.) is one of the basic structures...

In mathematics, measure theory in topological vector spaces refers to the extension of measure theory to topological vector spaces. Such spaces are often...

In functional analysis and related areas of mathematics, locally convex topological vector spaces (LCTVS) or locally convex spaces are examples of topological...

combination, while signed measures are the linear closure of positive measures. More generally see measure theory in topological vector spaces. Another generalization...

put it more abstractly every seminormed vector space is a topological vector space and thus carries a topological structure which is induced by the semi-norm...

In gauge theory and mathematical physics, a topological quantum field theory (or topological field theory or TQFT) is a quantum field theory that computes...

topological spaces. The idea of the definition of a Radon measure is to find some properties that characterize the measures on locally compact spaces...

topological dual space, or just dual space (in the sense of the theory of topological vector spaces) V ′ {\displaystyle V'} is defined as the space of...

1910). Lp spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical...

case of topological vector spaces, which include function spaces, inner product spaces, normed spaces, Hilbert spaces and Banach spaces. In this article...

In mathematics, topological groups are the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time,...

complete normed space, Hilbert spaces are by definition also Banach spaces. As such they are topological vector spaces, in which topological notions like...

is the notion of a complete topological vector space (TVS) or TVS-completeness, which uses the theory of uniform spaces. Specifically, the notion of...

In mathematics, nuclear spaces are topological vector spaces that can be viewed as a generalization of finite-dimensional Euclidean spaces and share many...

metric and topological spaces. Oxford University Press. ISBN 0-19-853161-3. Zbl 0304.54002. Trèves, François (2006) [1967]. Topological Vector Spaces, Distributions...

parent space which retains the same structure. While modern mathematics uses many types of spaces, such as Euclidean spaces, linear spaces, topological spaces...

techniques to bring function spaces as topological vector spaces within reach of the ideas that would apply to normed spaces of finite dimension. Here we...

authors use the term topologically complete for a wider class of topological spaces, the completely uniformizable spaces. A topological space homeomorphic to...

every connected topological manifold can be calculated. A connected topological manifold is locally homeomorphic to Euclidean n-space, in which the number...

than a topological space. Uniform spaces are spaces in which distances are not defined, but uniform continuity is. Approach spaces are spaces in which...

topological vector space is locally convex if and only if its topology is induced by a family of seminorms. Let X {\displaystyle X} be a vector space...

In mathematics, and especially differential geometry and mathematical physics, gauge theory is the general study of connections on vector bundles, principal...

Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces...

usually agree in a metric space, but may not be equivalent in other topological spaces. One such generalization is that a topological space is sequentially...

In mathematical analysis, the Haar measure assigns an "invariant volume" to subsets of locally compact topological groups, consequently defining an integral...

the case of topological vector spaces, which include function spaces, inner product spaces, normed spaces, Hilbert spaces and Banach spaces. Every algebra...

into a complete metric topological vector space. These spaces are of great interest in functional analysis, probability theory and harmonic analysis....

spaces have wide-ranging applications. They are important in measure theory, in that important results are special cases of results for Riesz spaces....

in the same way that a topological space possesses the minimum amount of structure needed to address questions of continuity. Bornological spaces are...

In mathematics, the tensor product V ⊗ W {\displaystyle V\otimes W} of two vector spaces V {\displaystyle V} and W {\displaystyle W} (over the same field)...