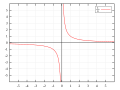
In mathematics, particularly in the area of arithmetic, a modular multiplicative inverse of an integer a is an integer x such that the product ax is congruent...

mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity...

With that provision, x is the modular multiplicative inverse of a modulo b, and y is the modular multiplicative inverse of b modulo a. Similarly, the...

a modular multiplicative inverse of a modulo m. If a ≡ b (mod m) and a−1 exists, then a−1 ≡ b−1 (mod m) (compatibility with multiplicative inverse, and...

remainder of c = 8. Modular exponentiation can be performed with a negative exponent e by finding the modular multiplicative inverse d of b modulo m using...

to multiplication, apn−1 = 1 (for a ≠ 0), thus the inverse of a is apn−2. This algorithm is a generalization of the modular multiplicative inverse based...

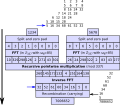
In modular arithmetic computation, Montgomery modular multiplication, more commonly referred to as Montgomery multiplication, is a method for performing...

public key. Determine d as d ≡ e−1 (mod λ(n)); that is, d is the modular multiplicative inverse of e modulo λ(n). This means: solve for d the equation de ≡...

has nonnegative valuation. The integer a can be computed as a modular multiplicative inverse: a = n d − 1 mod ⁡ p {\displaystyle a=nd^{-1}\operatorname {mod}...

{\frac {a}{b}}} does not denote the modular multiplication of a {\displaystyle a} times the modular multiplicative inverse of b {\displaystyle b} but rather...

Fermat's little theorem. Inverse: [(−a mod n) + (a mod n)] mod n = 0. b−1 mod n denotes the modular multiplicative inverse, which is defined if and only...

every nonzero element a has a unique modular multiplicative inverse, a−1 such that aa−1 = a−1a ≡ 1 mod m. This inverse can be found by solving the congruence...

the multiplication is associative, commutative, and that the class of 1 is the unique multiplicative identity. Finally, given a, the multiplicative inverse...

Inversive congruential generators are a type of nonlinear congruential pseudorandom number generator, which use the modular multiplicative inverse (if...

(related through the identity |−x| = |x|). Monoid Inverse function Involution (mathematics) Multiplicative inverse Reflection (mathematics) Reflection symmetry...

subgroup of a multiplicative group of integers modulo  n {\displaystyle n} , where n {\displaystyle n} is prime, the modular multiplicative inverse can be computed...

\ 1{\pmod {n}}} . In other words, the multiplicative order of a modulo n is the order of a in the multiplicative group of the units in the ring of the...

\cdot \right)} ⁠, the rationals with multiplication, being a group: because zero does not have a multiplicative inverse (i.e., there is no x {\displaystyle...

mod p, which matches C′ · y, since Peggy multiplied by the modular multiplicative inverse of y. However, if in either one of the above scenarios Victor...

the extended Euclidean algorithm http://en.wikipedia.org/wiki/Modular_multiplicative_inverse#Computation """ x = 0 last_x = 1 y = 1 last_y = 0 while b !=...

(fields do not form an algebra, since zero does not have a multiplicative inverse). The inverse limit can be defined abstractly in an arbitrary category...

This formula still holds after a modular reduction if a modular multiplicative inverse is used to compute ( a d − b c ) − 1 {\displaystyle...

is a positive fraction with one as its numerator, 1/n. It is the multiplicative inverse (reciprocal) of the denominator of the fraction, which must be a...

{\displaystyle D(x)=a^{-1}(x-b){\bmod {m}}} where a−1 is the modular multiplicative inverse of a modulo m. I.e., it satisfies the equation 1 = a a − 1 mod...

{\displaystyle \gcd(R,m)=1,} let R − 1 {\displaystyle R^{-1}} be the modular multiplicative inverse of R {\displaystyle R} (i.e., 0 < R − 1 < m {\displaystyle 0<R^{-1}<m}...

multiplication say that Z {\displaystyle \mathbb {Z} } under multiplication is a commutative monoid. However, not every integer has a multiplicative inverse...

{1}{n}}\equiv 2^{-m}{\bmod {N}}(n)} , where m is found using the modular multiplicative inverse. In Schönhage–Strassen algorithm, N = 2 M + 1 {\displaystyle...

relating to Fermat's little theorem RSA Table of congruences Modular multiplicative inverse Long 1972, pp. 87–88. Pettofrezzo & Byrkit 1970, pp. 110–111...

In mathematics, in particular in the theory of modular forms, a Hecke operator, studied by Erich Hecke (1937a,1937b), is a certain kind of "averaging"...

homomorphism is a function f : R → S that preserves addition, multiplication and multiplicative identity; that is, f ( a + b ) = f ( a ) + f ( b ) , f ( a...