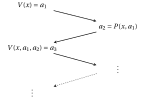
complements of all problems in PSPACE are also in PSPACE, meaning that co-PSPACE = PSPACE. The following relations are known between PSPACE and the complexity classes...

In computational complexity theory, a decision problem is PSPACE-complete if it can be solved using an amount of memory that is polynomial in the input...

problems solvable by an interactive proof system. It is equal to the class PSPACE. The result was established in a series of papers: the first by Lund, Karloff...

Second-order logic with a transitive closure (commutative or not) yields PSPACE, the problems solvable in polynomial space. Second-order logic with a least...

basic time and space complexity classes in the following way: P ⊆ NP ⊆ PSPACE ⊆ EXPTIME ⊆ NEXPTIME ⊆ EXPSPACE. Furthermore, by the time hierarchy theorem...

is contained in PSPACE, which also proves that QIP = IP = PSPACE, since PSPACE is easily shown to be in QIP using the result IP = PSPACE. Watrous, John...

hypothetical technologies List of NP-complete problems List of paradoxes List of PSPACE-complete problems List of undecidable problems List of unsolved deaths Lists...

interactive proofs, and the quantum analogue of the celebrated result IP = PSPACE: QIP = PSPACE. This was preceded by a series of results, showing QIP can be constrained...

exponential time, a very large class. NEXPTIME contains PSPACE, and is believed to strictly contain PSPACE. Adding a constant number of additional provers beyond...

the classes NP and co-NP. Each class in the hierarchy is contained within PSPACE. The hierarchy can be defined using oracle machines or alternating Turing...

PSPACE {\displaystyle {\textsf {P}}\subseteq {\textsf {NP}}\subseteq {\textsf {PP}}\subseteq {\textsf {PSPACE}}} , but it is possible that P = PSPACE...

than PSPACE, the class of problems decidable in polynomial space. PSPACE is equivalent to NPSPACE by Savitch's theorem. Again, whether P = PSPACE is an...

need not store game states; however many games of interest are known to be PSPACE-hard, and it follows that their space complexity will be lower-bounded by...

Here are some of the more commonly known problems that are PSPACE-complete when expressed as decision problems. This list is in no way comprehensive. Generalized...

1145/321978.321989. S2CID 8845949. Stefan Reisch (1981). "Hex ist PSPACE-vollständig (Hex is PSPACE-complete)". Acta Informatica. 15 (2): 167–191. doi:10.1007/bf00288964...

use O ( f ( n ) ) {\displaystyle O(f(n))} space. The complexity classes PSPACE and NPSPACE allow f {\displaystyle f} to be any polynomial, analogously...

\exists z\ ((x\lor z)\land y)} QBF is the canonical complete problem for PSPACE, the class of problems solvable by a deterministic or nondeterministic Turing...

complexity. Without ko, Go is PSPACE-hard. This is proved by reducing True Quantified Boolean Formula, which is known to be PSPACE-complete, to generalized...

is in EXPSPACE, and is PSPACE-hard. It's proved to be PSPACE-hard by reducing Generalized Geography, a problem known to be PSPACE-hard, to a game of Ghost...

complexity classes relate to each other in the following way: L⊆NL⊆P⊆NP⊆PSPACE⊆EXPTIME⊆NEXPTIME⊆EXPSPACE Where ⊆ denotes the subset relation. However,...

win for the first player in a given position is PSPACE-complete. Generalized hex and reversi are PSPACE-complete. For many generalized games which may...

computational problem that is known to be NP-hard and in PSPACE, but is not known to be complete for NP, PSPACE, or any language in the polynomial hierarchy. ∃...

prove that IP = PSPACE. However, in 2008, Scott Aaronson and Avi Wigderson showed that the main technical tool used in the IP = PSPACE proof, known as...

⁠ is symmetrical. co-NP is a subset of PH, which itself is a subset of PSPACE. An example of a problem that is known to belong to both NP and co-NP (but...

computational complexity theory, generalized geography is a well-known PSPACE-complete problem. Geography is a children's game, where players take turns...

ignoring the proof and solving it. NP is contained in PSPACE—to show this, it suffices to construct a PSPACE machine that loops over all proof strings and feeds...

removing all tiles is PSPACE-complete, and the game is NP-complete if looking below tiles is allowed. It has been proven that it is PSPACE-hard to approximate...

PP\subseteq PSPACE\subseteq EXP}}} As the problem of ⁠ P   = ?   P S P A C E {\displaystyle {\mathsf {P}}\ {\stackrel {?}{=}}\ {\mathsf {PSPACE}}} ⁠ has...

Arthur can interact for k rounds. QMA is QIP(1). QIP(2) is known to be in PSPACE. QIP is QIP(k) where k is allowed to be polynomial in the number of qubits...

configuration) is PSPACE-complete. This can be proved in two ways. The first way is by reducing a generalized Hex position, which is known to be PSPACE-complete...