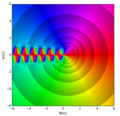
In mathematics, the polygamma function of order m is a meromorphic function on the complex numbers C {\displaystyle \mathbb {C} } defined as the (m +...

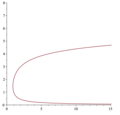
In mathematics, the generalized polygamma function or balanced negapolygamma function is a function introduced by Olivier Espinosa Aldunate and Victor...

(z)={\frac {\Gamma '(z)}{\Gamma (z)}}.} It is the first of the polygamma functions. This function is strictly increasing and strictly concave on ( 0 , ∞ ) {\displaystyle...

The polygamma identities can be used to obtain a multiplication theorem for harmonic numbers. The Hurwitz zeta function generalizes the polygamma function...

tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function. The Clausen function of order 2 – often...

where ψ {\displaystyle \psi } and γ {\displaystyle \gamma } are the polygamma function and Euler's constant, respectively, as well as ∑ n = 1 ∞ ζ ( 2 n )...

of the gamma function is called the digamma function; higher derivatives are the polygamma functions. The analog of the gamma function over a finite...

Riemann zeta function. Γ ( z ) {\displaystyle \Gamma (z)} is the gamma function. ψ n ( z ) {\displaystyle \psi _{n}(z)} is a polygamma function. Li s ⁡ (...

analogue. Digamma function, Polygamma function Incomplete beta function Incomplete gamma function K-function Multivariate gamma function: A generalization...

Also the series representation of Dirichlet beta function can be formed in terms of the polygamma function β ( s ) = 1 2 s ∑ n = 0 ∞ ( − 1 ) n ( n + 1 2...

In mathematics, the trigamma function, denoted ψ1(z) or ψ(1)(z), is the second of the polygamma functions, and is defined by ψ 1 ( z ) = d 2 d z 2 ln ⁡...

q)=\sum _{k=0}^{\infty }(k+q)^{-s}} Another expression using the polygamma function is K ( z ) = exp ⁡ [ ψ ( − 2 ) ( z ) + z 2 − z 2 − z 2 ln ⁡ 2 π ]...

S2CID 193082268. Weisstein, Eric W. "Polygamma Function". mathworld.wolfram.com. Retrieved 2025-02-08. A special function mostly commonly denoted ψ_n(z), ψ^((n))(z)...

Chebyshev function ψ ( x ) {\displaystyle \psi (x)} the polygamma function ψ m ( z ) {\displaystyle \psi ^{m}(z)} or its special cases the digamma function ψ...

gamma function Γ ( z ) {\textstyle \Gamma (z)} , due to Leonhard Euler. There is also a reflection formula for the general n-th order polygamma function ψ(n)(z)...

uniform electric field. The Hurwitz zeta function with a positive integer m is related to the polygamma function: ψ ( m ) ( z ) = ( − 1 ) m + 1 m ! ζ (...

{z}{2^{s}}}\Phi (-z^{2},s,{\tfrac {1}{2}})} The polygamma functions for positive integers n: ψ ( n ) ( α ) = ( − 1 ) n + 1 n ! Φ ( 1...

the polygamma function of order 2 k {\displaystyle 2k} . The Riemann–Siegel theta function is of interest in studying the Riemann zeta function, since...

needed] The digamma function, and by extension the polygamma function, is defined in terms of the logarithmic derivative of the gamma function. Generalizations...

(also falling, lower, rising, upper factorials) Poisson distribution Polygamma function Primorial Proof of Bertrand's postulate Sierpinski triangle Star of...

the stream function in fluid dynamics the reciprocal Fibonacci constant the second Chebyshev function in number theory the polygamma function in mathematics...

1)\psi ^{0}(k/2))} where ψ 0 ( z ) {\displaystyle \psi ^{0}(z)} is the polygamma function. We find the large n=k+1 approximation of the mean and variance of...

{1}{z^{4}}}\right)\,,} where ψ ( n ) ( x ) {\displaystyle \psi ^{(n)}(x)} is the polygamma function. Borwein, Jonathan M.; Corless, Robert M. (2017). "Gamma and Factorial...

the trigamma function, denoted ψ1(α), is the second of the polygamma functions, and is defined as the derivative of the digamma function: ψ 1 ( α ) =...

{t}{1-t}}\right]} which holds for |t| < 2. Here, ψ is the digamma function and ψ(m) is the polygamma function. Many series involving the binomial coefficient may be...

integer, and m > 1 {\displaystyle m>1} integer or not, we have from polygamma functions: H q / p , m = ζ ( m ) − p m ∑ k = 1 ∞ 1 ( q + p k ) m {\displaystyle...

_{p}(a)}{\partial a}}=\sum _{i=1}^{p}\psi (a+(1-i)/2),} and the general polygamma function as ψ p ( n ) ( a ) = ∂ n log ⁡ Γ p ( a ) ∂ a n = ∑ i = 1 p ψ ( n )...

Melchior Islands, Antarctica Chebyshev function Dedekind psi function Digamma function Polygamma functions Stream function, in two-dimensional flows Polar tangential...

(\alpha )} is strictly concave, by using inequality properties of the polygamma function. Finding the maximum with respect to α by taking the derivative and...

parameter ξ {\displaystyle \xi } only through the polygamma function of order 1 (also called the trigamma function): V a r [ Y ] = { ψ ′ ( 1 ) − ψ ′ ( − 1 / ξ...