Polynomial Matrix Spectral Factorization or Matrix Fejer–Riesz Theorem is a tool used to study the matrix decomposition of polynomial matrices. Polynomial...

characteristic polynomial to zero. In spectral graph theory, the characteristic polynomial of a graph is the characteristic polynomial of its adjacency matrix. In...

linear algebra, eigendecomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues...

Non-negative matrix factorization (NMF or NNMF), also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra...

square matrix is invertible if and only if it has a nonzero determinant and the eigenvalues of a square matrix are the roots of a polynomial determinant...

square root may be used for any factorization of a positive semidefinite matrix A as BTB = A, as in the Cholesky factorization, even if BB ≠ A. This distinct...

analysis, a spectral theorem is a result about when a linear operator or matrix can be diagonalized (that is, represented as a diagonal matrix in some basis)...

decomposition or Cholesky factorization (pronounced /ʃəˈlɛski/ shə-LES-kee) is a decomposition of a Hermitian, positive-definite matrix into the product of...

multiplication operator by a trigonometric polynomial, compressed to a finite-dimensional space, can be represented by such a matrix. Similarly, one can represent...

the FFT as a recursive factorization of the polynomial z n − 1 {\displaystyle z^{n}-1} , here into real-coefficient polynomials of the form z m − 1 {\displaystyle...

adjacency matrix of a perfect matching is a symmetric permutation matrix. A perfect matching is also called a 1-factor; see Graph factorization for an explanation...

Schur, is a matrix decomposition. It allows one to write an arbitrary complex square matrix as unitarily similar to an upper triangular matrix whose diagonal...

representation. Such an approach is called a spectral method. Suppose we wish to compute the polynomial product c(x) = a(x) · b(x). The ordinary product...

offer a major advantage: the results of matrix arithmetic operations like matrix multiplication, factorization or inversion can be approximated in O (...

sparse Cholesky, and other factorization methods) can be sufficient for meshes with a hundred thousand vertices. The matrix L {\displaystyle L} is usually...

In mathematics, the Zernike polynomials are a sequence of polynomials that are orthogonal on the unit disk. Named after optical physicist Frits Zernike...

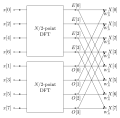
Note that the characteristic polynomial of the above DFT matrix may not split over F q {\displaystyle F_{q}} . The DFT matrix is order 4. We may need to...

self-intersection in the complex plane), a Riemann–Hilbert factorization problem is the following. Given a matrix function G ( t ) {\displaystyle G(t)} defined on...

from a p-variate Wishart distribution with scale matrix V and n degrees of freedom is the factorization: X = L A A T L T , {\displaystyle \mathbf {X} ={\textbf...

The Herglotzian definition yields polynomials which may, if one wishes, be further factorized into a polynomial of z {\displaystyle z} and another of...

ax + by = c Integer factorization: breaking an integer into its prime factors Congruence of squares Dixon's algorithm Fermat's factorization method General...

the unit disc as a spectral set. Sz.-Nagy & Foiaş 1970, 3.1. Constantinescu, T. (1996), Schur Parameters, Dilation and Factorization Problems, vol. 82...

applications to cyclotomic polynomials (and their logarithms). The referenced article by Mousavi and Schmidt (2017) develops a factorization-theorem-like treatment...

inverse covariance matrix of x {\displaystyle \mathbf {x} } . The Tikhonov matrix is then given as a factorization of the matrix Q = Γ T Γ {\displaystyle...

1-factorable. The perfect 1-factorization conjecture that every complete graph on an even number of vertices admits a perfect 1-factorization. Cereceda's conjecture...

differential operators. Spectral graph theory the study of properties of a graph using methods from matrix theory. Spectral theory part of operator theory...

2016-03-03, retrieved 2010-06-08 Shor, Peter W. (1997), "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer", SIAM...

matrix RRQR factorization — rank-revealing QR factorization, can be used to compute rank of a matrix Polar decomposition — unitary matrix times positive-semidefinite...

In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum...

precision arithmetic. Examples include Gaussian elimination, the QR factorization method for solving systems of linear equations, and the simplex method...