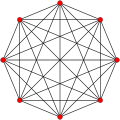
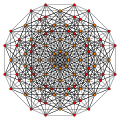
six-dimensional geometry, a runcinated 6-simplex is a convex uniform 6-polytope constructed as a runcination (3rd order truncations) of the regular 6-simplex. There...

and cantellations. Runcinated hexateron Small prismated hexateron (Acronym: spix) (Jonathan Bowers) The vertices of the runcinated 5-simplex can be most...

In seven-dimensional geometry, a runcinated 7-simplex is a convex uniform 7-polytope with 3rd order truncations (runcination) of the regular 7-simplex...

Runcinated enneazetton Small prismated enneazetton (Acronym: spene) (Jonathan Bowers) The Cartesian coordinates of the vertices of the runcinated 8-simplex...

series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes (equilateral triangles and squares in the case of the...

Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math...

hyperplane is a runcinated 5-cell. This cross-section divides the stericated hexateron into two pentachoral hypercupolas consisting of 6 5-cells, 15 tetrahedral...

a 7-polytope is a polytope contained by 6-polytope facets. Each 5-polytope ridge being shared by exactly two 6-polytope facets. A uniform 7-polytope is...

series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes (tetrahedrons and octahedrons in the case of the rectified...

polyhedron, {4,6|3}, is similarly related to the square faces of the runcinated 5-cell. The disphenoidal 30-cell is the dual of the bitruncated 5-cell...

unless it is all 5 vertices. It is impossible to rotate two concentric 4-simplexes with respect to each other such that some, but not all, of their vertices...