The Tonelli–Shanks algorithm (referred to by Shanks as the RESSOL algorithm) is used in modular arithmetic to solve for r in a congruence of the form...

Tonelli may refer to: Tonelli (surname) Tonelli (film), a 1943 German film Tonelli's theorem (functional analysis) Tonelli's theorem Tonelli–Shanks algorithm...

Shanks' square forms factorization is a method for integer factorization devised by Daniel Shanks as an improvement on Fermat's factorization method....

method that generalizes Fermat's factorization method; and the Tonelli–Shanks algorithm that finds square roots modulo a prime, which is useful for the...

finding algorithm Cipolla's algorithm Tonelli–Shanks algorithm Multiplication algorithms: fast multiplication of two numbers Karatsuba algorithm Schönhage–Strassen...

{\displaystyle k-1} times. For this, Cipolla's algorithm is better than the Tonelli–Shanks algorithm if and only if S ( S − 1 ) > 8 m + 20 {\displaystyle...

the generalized Riemann hypothesis holds as explained for the Tonelli–Shanks algorithm. Given an odd prime p {\displaystyle p} in the form 4 k + 1 {\displaystyle...

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers...

Pollard's rho algorithm is an algorithm for integer factorization. It was invented by John Pollard in 1975. It uses only a small amount of space, and...

and computer programming, the extended Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common...

Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor...

In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking...

found will quickly produce one. A slight variant of this algorithm is the Tonelli–Shanks algorithm. If the modulus n is a prime power n = pe, a solution...

sieve Shanks's square forms factorization (SQUFOF) Shor's algorithm, for quantum computers In number theory, there are many integer factoring algorithms that...

multiplication algorithm is an algorithm (or method) to multiply two numbers. Depending on the size of the numbers, different algorithms are more efficient...

In computational number theory, the index calculus algorithm is a probabilistic algorithm for computing discrete logarithms. Dedicated to the discrete...

The Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers, published by Arnold Schönhage and Volker Strassen...

y {\displaystyle y} and k {\displaystyle k} be non-negative integers. Algorithms that compute (the decimal representation of) y {\displaystyle {\sqrt {y}}}...

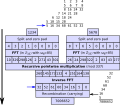
The Karatsuba algorithm is a fast multiplication algorithm for integers. It was discovered by Anatoly Karatsuba in 1960 and published in 1962. It is a...

The binary GCD algorithm, also known as Stein's algorithm or the binary Euclidean algorithm, is an algorithm that computes the greatest common divisor...

Pollard's rho algorithm for logarithms is an algorithm introduced by John Pollard in 1978 to solve the discrete logarithm problem, analogous to Pollard's...

composite return probably prime Using fast algorithms for modular exponentiation, the running time of this algorithm is O(k·log3 n), where k is the number...

A primality test is an algorithm for determining whether an input number is prime. Among other fields of mathematics, it is used for cryptography. Unlike...

Lenstra–Lenstra–Lovász (LLL) lattice basis reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and...

meet-in-the-middle algorithm for computing the discrete logarithm or order of an element in a finite abelian group by Daniel Shanks. The discrete log problem...

or Rabin–Miller primality test is a probabilistic primality test: an algorithm which determines whether a given number is likely to be prime, similar...

A division algorithm is an algorithm which, given two integers N and D (respectively the numerator and the denominator), computes their quotient and/or...

|a|. This case is important as the terminating step of the Euclidean algorithm. The above definition is unsuitable for defining gcd(0, 0), since there...

theory, Williams's p + 1 algorithm is an integer factorization algorithm, one of the family of algebraic-group factorisation algorithms. It was invented by...

elliptic-curve factorization method (ECM) is a fast, sub-exponential running time, algorithm for integer factorization, which employs elliptic curves. For general-purpose...