Interval arithmetic (also known as interval mathematics; interval analysis or interval computation) is a mathematical technique used to mitigate rounding...

image of an interval by a continuous function is an interval; integrals of real functions are defined over an interval; etc. Interval arithmetic consists...

half-open intervals are defined by removing the respective endpoints. This redefinition is useful in interval arithmetic when dividing by an interval containing...

example, the sequence "ABBCAB" could become 0.0112013, in arithmetic coding as a value in the interval [0, 1). The next step is to encode this ternary number...

being derivative of Gustafson's work on unums and interval arithmetic. "Floating decimal point arithmetic control means for calculator: United States Patent...

mathematical objects other than numbers, such as interval arithmetic and matrix arithmetic. Arithmetic operations form the basis of many branches of mathematics...

of intervals approximating r {\displaystyle r} . This allows the basic arithmetic operations on the real numbers to be defined in terms of interval arithmetic...

arithmetic Floating-point arithmetic Interval arithmetic Arbitrary-precision arithmetic Modular arithmetic Multi-modular arithmetic p-adic arithmetic...

approaches: (1) interval arithmetic approach; and (2) the extension principle approach. A fuzzy number is equal to a fuzzy interval. The degree of fuzziness...

yielding so-called interval arithmetics. Let us now consider the following very simple program: y = x; z = x - y; With reasonable arithmetic types, the result...

alpha theory, while a typical example of a priori certification is interval arithmetic. A certificate for a root is a computational proof of the correctness...

extensions of Heyting arithmetic by types including N N {\displaystyle {\mathbb {N} }^{\mathbb {N} }} , constructive second-order arithmetic, or strong enough...

computation. Affine arithmetic is meant to be an improvement on interval arithmetic (IA), and is similar to generalized interval arithmetic, first-order Taylor...

In computing, floating-point arithmetic (FP) is arithmetic on subsets of real numbers formed by a significand (a signed sequence of a fixed number of...

The IEEE Standard for Floating-Point Arithmetic (IEEE 754) is a technical standard for floating-point arithmetic originally established in 1985 by the...

implies that N(Y) is well defined and is an interval (see interval arithmetic for further details on interval operations). This naturally leads to the following...

example, the interval class between pitch classes 4 and 9 is 5 because 9 − 4 = 5 is less than 4 − 9 = −5 ≡ 7 (mod 12). See modular arithmetic for more on...

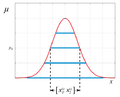
In statistics, a confidence interval (CI) is a range of values used to estimate an unknown statistical parameter, such as a population mean. Rather than...

numerical analysis. For computation, interval arithmetic is most often used, where all results are represented by intervals. Validated numerics were used by...

In mathematics and statistics, the arithmetic mean ( /ˌærɪθˈmɛtɪk/ arr-ith-MET-ik), arithmetic average, or just the mean or average (when the context...

False precision Guard digit IEEE 754 (IEEE floating-point standard) Interval arithmetic Kahan summation algorithm Precision (computer science) Round-off...

of seconds elapsed since 1970-01-01T00:00:10 TAI. This makes time interval arithmetic much easier. Time values from these systems do not suffer the ambiguity...

real numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean of ⁠ n {\displaystyle n}...

higher-order arithmetic: on one hand, when restricted to countable covers/the language of second-order arithmetic, the compactness of the unit interval is provable...

INTLAB (INTerval LABoratory) is an interval arithmetic library using MATLAB and GNU Octave, available in Windows and Linux, macOS. It was developed by...

in numerical analysis, including the computer implementation of interval arithmetic. After graduation from high school in Freising, Kulisch studied mathematics...

proposed using interval arithmetic with a pair of unums, what he called a ubound, providing the guarantee that the resulting interval contains the exact...

best one found so far by the algorithm. Interval arithmetic, interval mathematics, interval analysis, or interval computation, is a method developed by...

The term arithmetic underflow (also floating-point underflow, or just underflow) is a condition in a computer program where the result of a calculation...

on relational interval arithmetic developed at Bell-Northern Research in the 1980s and 1990s. Embedding relational interval arithmetic in a logic programming...