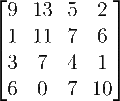algebra, an invertible matrix (non-singular, non-degenarate or regular) is a square matrix that has an inverse. In other words, if some other matrix is multiplied...

general linear group of all invertible matrices. A triangular matrix is invertible precisely when its diagonal entries are invertible (non-zero). Over the real...

matrix A {\displaystyle A}  is called diagonalizable or non-defective if it is similar to a diagonal matrix. That is, if there exists an invertible matrix...

invertible matrices is again invertible, and the inverse of an invertible matrix is invertible, with the identity matrix as the identity element of the...

an invertible element is an element that has an inverse. In a ring, an invertible element, also called a unit, is an element that is invertible under...

defined using the Leibniz formula; such a matrix is invertible if and only if its determinant is invertible in R, generalizing the situation over a field...

in particular linear algebra, the matrix determinant lemma computes the determinant of the sum of an invertible matrix A and the dyadic product, u vT, of...

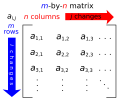
m\times n} matrix A {\displaystyle A} . A square matrix A {\displaystyle A} is called invertible or non-singular if there exists a matrix B {\displaystyle...

,} where I is the identity matrix of the same size as A. Consequently, the multiplicative inverse of an invertible matrix can be found by dividing its...

A singular matrix is a square matrix that is not invertible, unlike non-singular matrix which is invertible. Equivalently, an n {\displaystyle n} -by-...

an invertible matrix B {\displaystyle B} with conjugate transpose B ∗ {\displaystyle B^{*}} such that M = B ∗ B . {\displaystyle M=B^{*}B.} A matrix is...

identity matrix. Involutory matrices are all square roots of the identity matrix. This is a consequence of the fact that any invertible matrix multiplied...

{T} }=Q^{-1},} where Q−1 is the inverse of Q. An orthogonal matrix Q is necessarily invertible (with inverse Q−1 = QT), unitary (Q−1 = Q∗), where Q∗ is the...

{2}}\end{bmatrix}}.} An invertible matrix A is a generalized permutation matrix if and only if it can be written as a product of an invertible diagonal matrix D and an...

words, the matrix of the combined transformation A followed by B is simply the product of the individual matrices. When A is an invertible matrix there is...

The transpose of an invertible matrix is also invertible, and its inverse is the transpose of the inverse of the original matrix. The notation A−T is...

inverse of a "rank-1 update" to a matrix whose inverse has previously been computed. That is, given an invertible matrix A {\displaystyle A} and the outer...

represented, on a given basis, by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the corresponding linear map...

an invertible matrix. Most rotation matrices fit this description, and for them it can be shown that (Q − I)(Q + I)−1 is a skew-symmetric matrix, A....

a unimodular matrix M is a square integer matrix having determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers:...

n-by-n matrices A and B are called similar if there exists an invertible n-by-n matrix P such that B = P − 1 A P . {\displaystyle B=P^{-1}AP.} Similar...

congruent if there exists an invertible matrix P over the same field such that PTAP = B where "T" denotes the matrix transpose. Matrix congruence is an equivalence...

the inverse of an invertible matrix. The method is named after Carl Friedrich Gauss (1777–1855). To perform row reduction on a matrix, one uses a sequence...

Invertible may refer to Invertible element Invertible function Invertible ideal Invertible knot Invertible jet Invertible matrix Invertible module Invertible...

matrix similarity. The row echelon form is a canonical form, when one considers as equivalent a matrix and its left product by an invertible matrix....

λi+1)vi+1 = vi and βi = 0 otherwise. More generally, if W is any invertible matrix, and λ is an eigenvalue of A with generalized eigenvector v, then...

=\mathbf {I} .} A matrix that has an inverse is an invertible matrix. Otherwise, it is a singular matrix. A product of matrices is invertible if and only if...

of a Lie algebra, when the Lie algebra is gln Invertible matrix (this usage is rare) QS Regular Matrix, a quadraphonic sound system developed by Sansui...

A Stieltjes matrix is necessarily an M-matrix. Every n×n Stieltjes matrix is invertible to a nonsingular symmetric nonnegative matrix, though the converse...

In linear algebra, an invertible complex square matrix U is unitary if its matrix inverse U−1 equals its conjugate transpose U*, that is, if U ∗ U = U...