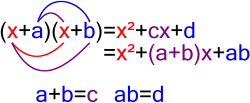In mathematics, the fundamental theorem of arithmetic, also called the unique factorization theorem and prime factorization theorem, states that every...

because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes...

in-and-of itself. Fundamental theorem of algebra Fundamental theorem of algebraic K-theory Fundamental theorem of arithmetic Fundamental theorem of Boolean...

the number of primes is infinite. Another proof, by the Swiss mathematician Leonhard Euler, relies on the fundamental theorem of arithmetic: that every...

common multiple of two or more fractions' denominators Factoring – Breaking a number down into its products Fundamental theorem of arithmetic Prime number...

factorization of polynomials Fundamental theorem of arithmetic, a theorem regarding prime factorization Fundamental analysis, the process of reviewing and analyzing...

property is the key in the proof of the fundamental theorem of arithmetic. It is used to define prime elements, a generalization of prime numbers to arbitrary...

render RSA-based public-key cryptography insecure. By the fundamental theorem of arithmetic, every positive integer has a unique prime factorization....

case of integers. They proved the fundamental theorem of arithmetic, which asserts that every positive integer may be factored into a product of prime...

theory may refer to: Prime number Prime number theorem Number theory Fundamental theorem of arithmetic, which explains prime factorization. This disambiguation...

Lasker–Noether theorem is an extension of the fundamental theorem of arithmetic, and more generally the fundamental theorem of finitely generated abelian groups...

group, meaning that much theory of such subgroups could be applied. Euclid's proof of the fundamental theorem of arithmetic is a simple proof which uses...

The unique factorization theorem is the fundamental theorem of arithmetic that relates to prime factorization. The theorem states that every integer...

Division theorem, the uniqueness of quotient and remainder under Euclidean division. Fundamental theorem of arithmetic, the uniqueness of prime factorization...

arithmetic for the hypotheses of the incompleteness theorem. Thus by the first incompleteness theorem, Peano Arithmetic is not complete. The theorem gives...

area of topology known as knot theory, there is an analogue of the fundamental theorem of arithmetic: the decomposition of a knot into a sum of prime...

fundamental theorem of arithmetic, Euclid's theorem, and Fermat's Last Theorem. According to the fundamental theorem of arithmetic, every integer greater...

The fundamental theorem of algebra, also called d'Alembert's theorem or the d'Alembert–Gauss theorem, states that every non-constant single-variable polynomial...

ring following the terminology of Bourbaki) is a ring in which a statement analogous to the fundamental theorem of arithmetic holds. Specifically, a UFD is...

correspond to ordered prime factorizations of n, and in fact yields a proof of the fundamental theorem of arithmetic. For example, the cyclic group C 12 {\displaystyle...

the set of the prime numbers as a basis (this results from the fundamental theorem of arithmetic). The center Z ( G ) {\displaystyle Z(G)} of a group...

the first time the fundamental theorem of arithmetic. Asas al-qawa'id fi usul al-fawa'id (The base of the rules in the principles of uses) which comprises...

the fundamental theorem of arithmetic. Thus, when considering abstract rings, a natural question to ask is under what conditions such a theorem holds...

element of a PID has a unique factorization into prime elements (so an analogue of the fundamental theorem of arithmetic holds); any two elements of a PID...

} The fundamental theorem of arithmetic states that any positive integer n can be represented uniquely as a product of powers of primes: n = p...

formal semantics. Informally, the theorem states that "arithmetical truth cannot be defined in arithmetic". The theorem applies more generally to any sufficiently...

fundamental theorem on homomorphisms, also known as the fundamental homomorphism theorem, or the first isomorphism theorem, relates the structure of two...

the fundamental theorem of arithmetic. Goldstein, Catherine (1992). "On a Seventeenth Century Version of the "Fundamental Theorem of Arithmetic"". Historia...

the fundamental theorem of arithmetic, every integer greater than 1 can be represented uniquely as a product of prime numbers, up to the order of the...

of n {\displaystyle n} is a product of prime divisors of n {\displaystyle n} raised to some power. This is a consequence of the fundamental theorem of...