mathematics, an uncountable set, informally, is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related...

In set theory, an infinite set is a set that is not a finite set. Infinite sets may be countable or uncountable. The set of natural numbers (whose existence...

elements than there are positive integers. Such sets are now called uncountable sets, and the size of infinite sets is treated by the theory of cardinal numbers...

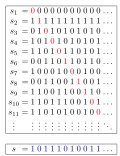
that the set of all real numbers is uncountably, rather than countably, infinite. This theorem is proved using Cantor's first uncountability proof, which...

Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. Although the terms...

and the set of rational numbers are all countable. A set is uncountable if it is both infinite and cannot be put in correspondence with the set of natural...

existence theorem that there are such sets. Each Vitali set is uncountable, and there are uncountably many Vitali sets. The proof of their existence depends...

"countably infinite". Sets with cardinality strictly greater than ℵ 0 {\displaystyle \aleph _{0}} are called uncountable sets. Cantor's diagonal argument...

study of the Mandelbrot set remains a key topic in the field of complex dynamics. The Mandelbrot set is the uncountable set of values of c in the complex...

{\displaystyle \operatorname {J} (f)} is a nowhere dense set (it is without interior points) and an uncountable set (of the same cardinality as the real numbers)...

contradiction that a countable model of first-order set theory could contain an uncountable set. The paradox arises from part of the Löwenheim–Skolem...

sizes of two sets by setting them in one-to-one correspondence. His "revolutionary discovery" was that the set of all real numbers is uncountable, that is...

as subsets of the real numbers. The Cantor set is an example of an uncountable null set. It is uncountable because it contains all real numbers between...

between sets, popularized by John Venn (1834–1923) in the 1880s. The diagrams are used to teach elementary set theory, and to illustrate simple set relationships...

Cantor set a universal probability space in some ways. In Lebesgue measure theory, the Cantor set is an example of a set which is uncountable and has...

core model and satisfies the covering property, that is for every uncountable set x of ordinals, there is y such that y ⊃ x, y has the same cardinality...

In set theory, the complement of a set A, often denoted by A c {\displaystyle A^{c}} (or A′), is the set of elements not in A. When all elements in the...

a set of reals with the perfect set property cannot be a counterexample to the continuum hypothesis, stated in the form that every uncountable set of...

compact nor countably metacompact, hence not compact. Uncountable set: On any uncountable set, such as the real numbers R {\displaystyle \mathbb {R}...

terms of closed sets; this is its most prominent application. Other applications include proving that certain perfect sets are uncountable, and the construction...

that, considered as a set, is uncountable. It is the supremum (least upper bound) of all countable ordinals. When considered as a set, the elements of ω...

be the set of Gödel numbers of the true sentences about the constructible universe, with c i {\displaystyle c_{i}} interpreted as the uncountable cardinal...

the empty set or void set is the unique set having no elements; its size or cardinality (count of elements in a set) is zero. Some axiomatic set theories...

to the first uncountable ordinal. To prove this claim, any open set in a metric space is the union of an increasing sequence of closed sets. In particular...

\end{cases}}} The set of all such indicator functions, { 1 r } r ∈ R {\displaystyle \{\mathbf {1} _{r}\}_{r\in \mathbb {R} }} , is an uncountable set indexed by...

In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in...

infinite set of components is covered formally by allowing n = ∞ {\displaystyle n=\infty \!} . Where the set of component distributions is uncountable, the...

cofinite topology defined on an infinite set, as is the cocountable topology defined on an uncountable set. Pseudometric spaces typically are not Hausdorff...

Naive set theory is any of several theories of sets used in the discussion of the foundations of mathematics. Unlike axiomatic set theories, which are...

the lower limit topology, no uncountable set is compact. In the cocountable topology on an uncountable set, no infinite set is compact. Like the previous...