Fourier transform

In physics, engineering and mathematics, the Fourier transform (FT) is an integral transform that takes as input a function and outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made the Fourier transform is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches.

The red sinusoid can be described by peak amplitude (1), peak-to-peak (2), RMS (3), and wavelength (4). The red and blue sinusoids have a phase difference of θ.

${\displaystyle \scriptstyle f(t)}$

${\displaystyle \scriptstyle {\widehat {f}}(\omega )}$

${\displaystyle \scriptstyle g(t)}$

${\displaystyle \scriptstyle {\widehat {g}}(\omega )}$

${\displaystyle \scriptstyle t}$

${\displaystyle \scriptstyle \omega }$

${\displaystyle \scriptstyle t}$

${\displaystyle \scriptstyle \omega }$

The top row shows a unit pulse as a function of time (f(t)) and its Fourier transform as a function of frequency (f̂(ω)). The bottom row shows a delayed unit pulse as a function of time (g(t)) and its Fourier transform as a function of frequency (ĝ(ω)). Translation (i.e. delay) in the time domain is interpreted as complex phase shifts in the frequency domain. The Fourier transform decomposes a function into eigenfunctions for the group of translations. The imaginary part of ĝ(ω) is negated because a negative sign exponent has been used in the Fourier transform, which is the default as derived from the Fourier series, but the sign does not matter for a transform that is not going to be reversed.

Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statistics as well as in the study of physical phenomena exhibiting normal distribution (e.g., diffusion). The Fourier transform of a Gaussian function is another Gaussian function. Joseph Fourier introduced the transform in his study of heat transfer, where Gaussian functions appear as solutions of the heat equation.

The Fourier transform can be formally defined as an improper Riemann integral, making it an integral transform, although this definition is not suitable for many applications requiring a more sophisticated integration theory.^{[note 1]} For example, many relatively simple applications use the Dirac delta function, which can be treated formally as if it were a function, but the justification requires a mathematically more sophisticated viewpoint.^{[note 2]}

The Fourier transform can also be generalized to functions of several variables on Euclidean space, sending a function of 3-dimensional 'position space' to a function of 3-dimensional momentum (or a function of space and time to a function of 4-momentum). This idea makes the spatial Fourier transform very natural in the study of waves, as well as in quantum mechanics, where it is important to be able to represent wave solutions as functions of either position or momentum and sometimes both. In general, functions to which Fourier methods are applicable are complex-valued, and possibly vector-valued.^{[note 3]} Still further generalization is possible to functions on groups, which, besides the original Fourier transform on R or Rⁿ, notably includes the discrete-time Fourier transform (DTFT, group = Z), the discrete Fourier transform (DFT, group = Z mod N) and the Fourier series or circular Fourier transform (group = S¹, the unit circle ≈ closed finite interval with endpoints identified). The latter is routinely employed to handle periodic functions. The fast Fourier transform (FFT) is an algorithm for computing the DFT.

Definition[edit]

The Fourier transform is an analysis process, decomposing a complex-valued function ${\displaystyle \textstyle f(x)}$ into its constituent frequencies and their amplitudes. The inverse process is synthesis, which recreates ${\displaystyle \textstyle f(x)}$ from its transform.

We can start with an analogy, the Fourier series, which analyzes ${\displaystyle \textstyle f(x)}$ on a bounded interval ${\displaystyle \textstyle x\in [-P/2,P/2],}$ for some positive real number ${\displaystyle P.}$ The constituent frequencies are a discrete set of harmonics at frequencies ${\displaystyle {\tfrac {n}{P}},n\in \mathbb {Z} ,}$ whose amplitude and phase are given by the analysis formula:

${\displaystyle c_{n}={\tfrac {1}{P}}\int _{-P/2}^{P/2}f(x)\,e^{-i2\pi {\frac {n}{P}}x}\,dx.}$

The actual Fourier series is the synthesis formula:

${\displaystyle f(x)=\sum _{n=-\infty }^{\infty }c_{n}\,e^{i2\pi {\tfrac {n}{P}}x},\quad \textstyle x\in [-P/2,P/2].}$

The analogy for a function ${\displaystyle \textstyle f(x)}$ can be obtained formally from the analysis formula by taking the limit as ${\displaystyle P\to \infty }$, while at the same time taking ${\displaystyle n}$ so that ${\displaystyle {\tfrac {n}{P}}\to \xi \in \mathbb {R} .}$^[1] (Kaiser 1994, p. 29), (Rahman 2011, p. 11). Formally carrying this out, we obtain, for rapidly decreasing ${\displaystyle f}$:^{[note 4][2]}

Fourier transform

${\displaystyle {\widehat {f}}(\xi )=\int _{-\infty }^{\infty }f(x)\ e^{-i2\pi \xi x}\,dx.}$

(Eq.1)

It is easy to see, assuming the hypothesis of rapid decreasing, that the integral Eq.1 converges for all real ${\displaystyle \xi }$, and (using the Riemann–Lebesgue lemma) that the transformed function ${\displaystyle {\widehat {f}}}$ is also rapidly decreasing. The validity of this definition for classes of functions ${\displaystyle f}$ that are not necessarily rapidly decreasing is discussed later in this section.

Evaluating Eq.1 for all values of ${\displaystyle \xi }$ produces the frequency-domain function. The complex number ${\displaystyle {\widehat {f}}(\xi )}$, in polar coordinates, conveys both amplitude and phase of frequency ${\displaystyle \xi .}$ The intuitive interpretation of Eq.1 is that the effect of multiplying ${\displaystyle f(x)}$ by ${\displaystyle e^{-i2\pi \xi x}}$ is to subtract ${\displaystyle \xi }$ from every frequency component of function ${\displaystyle f(x).}$^{[note 5]} Only the component that was at frequency ${\displaystyle \xi }$ can produce a non-zero value of the infinite integral, because (at least formally) all the other shifted components are oscillatory and integrate to zero. (see § Example)

The corresponding synthesis formula for such a function is:

Inverse transform

${\displaystyle f(x)=\int _{-\infty }^{\infty }{\widehat {f}}(\xi )\ e^{i2\pi \xi x}\,d\xi ,\quad \forall \ x\in \mathbb {R} .}$

(Eq.2)

Eq.2 is a representation of ${\displaystyle f(x)}$ as a weighted summation of complex exponential functions.

This is also known as the Fourier inversion theorem, and was first introduced in Fourier's Analytical Theory of Heat. ^{[3] [4] [5] [6]}

The functions ${\displaystyle f}$ and ${\displaystyle {\widehat {f}}}$ are referred to as a Fourier transform pair.^[7]  A common notation for designating transform pairs is:^[8]

${\displaystyle f(x)\ {\stackrel {\mathcal {F}}{\longleftrightarrow }}\ {\widehat {f}}(\xi ),}$   for example   ${\displaystyle \operatorname {rect} (x)\ {\stackrel {\mathcal {F}}{\longleftrightarrow }}\ \operatorname {sinc} (\xi ).}$

Definition for Lebesgue integrable functions[edit]

Until now, we have been dealing with Schwartz functions, which decay rapidly at infinity, with all derivatives. This excludes many functions of practical importance from the definition, such as the rect function. A measurable function ${\displaystyle f:\mathbb {R} \to \mathbb {C} }$ is called (Lebesgue) integrable if the Lebesgue integral of its absolute value is finite:

${\displaystyle \|f\|_{1}=\int _{\mathbb {R} }|f(x)|\,dx<\infty .}$

Two measurable functions are equivalent if they are equal except on a set of measure zero. The set of all equivalence classes of integrable functions is denoted ${\displaystyle L^{1}(\mathbb {R} )}$. Then:^[9]

The integral Eq.1 is well-defined for all ${\displaystyle \xi \in \mathbb {R} ,}$ because of the assumption ${\displaystyle \|f\|_{1}<\infty }$. (It can be shown that the function ${\displaystyle {\widehat {f}}\in L^{\infty }\cap C(\mathbb {R} )}$ is bounded and uniformly continuous in the frequency domain, and moreover, by the Riemann–Lebesgue lemma, it is zero at infinity.)

However, the class of Lebesgue integrable functions is not ideal from the point of view of the Fourier transform because there is no easy characterization of the image, and thus no easy characterization of the inverse transform.

Unitarity and definition for square integrable functions[edit]

While Eq.1 defines the Fourier transform for (complex-valued) functions in ${\displaystyle L^{1}(\mathbb {R} )}$, it is easy to see that it is not well-defined for other integrability classes, most importantly ${\displaystyle L^{2}(\mathbb {R} )}$. For functions in ${\displaystyle L^{1}\cap L^{2}(\mathbb {R} )}$, and with the conventions of Eq.1, the Fourier transform is a unitary operator with respect to the Hilbert inner product on ${\displaystyle L^{2}(\mathbb {R} )}$, restricted to the dense subspace of integrable functions. Therefore, it admits a unique continuous extension to a unitary operator on ${\displaystyle L^{2}(\mathbb {R} )}$, also called the Fourier transform. This extension is important in part because the Fourier transform preserves the space ${\displaystyle L^{2}(\mathbb {R} )}$ so that, unlike the case of ${\displaystyle L^{1}}$, the Fourier transform and inverse transform are on the same footing, being transformations of the same space of functions to itself.

Importantly, for functions in ${\displaystyle L^{2}}$, the Fourier transform is no longer given by Eq.1 (interpreted as a Lebesgue integral). For example, the function ${\displaystyle f(x)=(1+x^{2})^{-1/2}}$ is in ${\displaystyle L^{2}}$ but not ${\displaystyle L^{1}}$, so the integral Eq.1 diverges. In such cases, the Fourier transform can be obtained explicitly by regularizing the integral, and then passing to a limit. In practice, the integral is often regarded as an improper integral instead of a proper Lebesgue integral, but sometimes for convergence one needs to use weak limit or principal value instead of the (pointwise) limits implicit in an improper integral. Titchmarsh (1986) and Dym & McKean (1985) each gives three rigorous ways of extending the Fourier transform to square integrable functions using this procedure.

The conventions chosen in this article are those of harmonic analysis, and are characterized as the unique conventions such that the Fourier transform is both unitary on L² and an algebra homomorphism from L¹ to L^∞, without renormalizing the Lebesgue measure.^[10]

Angular frequency (ω)[edit]

When the independent variable (${\displaystyle x}$) represents time (often denoted by ${\displaystyle t}$), the transform variable (${\displaystyle \xi }$) represents frequency (often denoted by ${\displaystyle f}$). For example, if time is measured in seconds, then frequency is in hertz. The Fourier transform can also be written in terms of angular frequency, ${\displaystyle \omega =2\pi \xi ,}$ whose units are radians per second.

The substitution ${\displaystyle \xi ={\tfrac {\omega }{2\pi }}}$ into Eq.1 produces this convention, where function ${\displaystyle {\widehat {f}}}$ is relabeled ${\displaystyle {\widehat {f_{1}}}:}$

${\displaystyle {\begin{aligned}{\widehat {f_{3}}}(\omega )&\triangleq \int _{-\infty }^{\infty }f(x)\cdot e^{-i\omega \,x}\,dx={\widehat {f_{1}}}\left({\tfrac {\omega }{2\pi }}\right),\\f(x)&={\frac {1}{2\pi }}\int _{-\infty }^{\infty }{\widehat {f_{3}}}(\omega )\cdot e^{i\omega \,x}\,d\omega .\end{aligned}}}$

Unlike the Eq.1 definition, the Fourier transform is no longer a unitary transformation, and there is less symmetry between the formulas for the transform and its inverse. Those properties are restored by splitting the ${\displaystyle 2\pi }$ factor evenly between the transform and its inverse, which leads to another convention:

${\displaystyle {\begin{aligned}{\widehat {f_{2}}}(\omega )&\triangleq {\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(x)\cdot e^{-i\omega x}\,dx={\frac {1}{\sqrt {2\pi }}}\cdot {\widehat {f_{1}}}\left({\tfrac {\omega }{2\pi }}\right),\\f(x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }{\widehat {f_{2}}}(\omega )\cdot e^{i\omega x}\,d\omega .\end{aligned}}}$

Variations of all three conventions can be created by conjugating the complex-exponential kernel of both the forward and the reverse transform. The signs must be opposites.

Summary of popular forms of the Fourier transform, one-dimensional

ordinary frequency ξ (Hz)	unitary	${\displaystyle {\begin{aligned}{\widehat {f_{1}}}(\xi )\ &\triangleq \ \int _{-\infty }^{\infty }f(x)\,e^{-i2\pi \xi x}\,dx={\sqrt {2\pi }}\ \ {\widehat {f_{2}}}(2\pi \xi )={\widehat {f_{3}}}(2\pi \xi )\\f(x)&=\int _{-\infty }^{\infty }{\widehat {f_{1}}}(\xi )\,e^{i2\pi x\xi }\,d\xi \end{aligned}}}$
angular frequency ω (rad/s)	unitary	${\displaystyle {\begin{aligned}{\widehat {f_{2}}}(\omega )\ &\triangleq \ {\frac {1}{\sqrt {2\pi }}}\ \int _{-\infty }^{\infty }f(x)\,e^{-i\omega x}\,dx={\frac {1}{\sqrt {2\pi }}}\ \ {\widehat {f_{1}}}\!\left({\frac {\omega }{2\pi }}\right)={\frac {1}{\sqrt {2\pi }}}\ \ {\widehat {f_{3}}}(\omega )\\f(x)&={\frac {1}{\sqrt {2\pi }}}\ \int _{-\infty }^{\infty }{\widehat {f_{2}}}(\omega )\,e^{i\omega x}\,d\omega \end{aligned}}}$
	non-unitary	${\displaystyle {\begin{aligned}{\widehat {f_{3}}}(\omega )\ &\triangleq \ \int _{-\infty }^{\infty }f(x)\,e^{-i\omega x}\,dx={\widehat {f_{1}}}\left({\frac {\omega }{2\pi }}\right)={\sqrt {2\pi }}\ \ {\widehat {f_{2}}}(\omega )\\f(x)&={\frac {1}{2\pi }}\int _{-\infty }^{\infty }{\widehat {f_{3}}}(\omega )\,e^{i\omega x}\,d\omega \end{aligned}}}$

Generalization for n-dimensional functions

ordinary frequency ξ (Hz)	unitary	${\displaystyle {\begin{aligned}{\widehat {f_{1}}}(\xi )\ &\triangleq \ \int _{\mathbb {R} ^{n}}f(x)e^{-i2\pi \xi \cdot x}\,dx=(2\pi )^{\frac {n}{2}}{\widehat {f_{2}}}(2\pi \xi )={\widehat {f_{3}}}(2\pi \xi )\\f(x)&=\int _{\mathbb {R} ^{n}}{\widehat {f_{1}}}(\xi )e^{i2\pi \xi \cdot x}\,d\xi \end{aligned}}}$
angular frequency ω (rad/s)	unitary	${\displaystyle {\begin{aligned}{\widehat {f_{2}}}(\omega )\ &\triangleq \ {\frac {1}{(2\pi )^{\frac {n}{2}}}}\int _{\mathbb {R} ^{n}}f(x)e^{-i\omega \cdot x}\,dx={\frac {1}{(2\pi )^{\frac {n}{2}}}}{\widehat {f_{1}}}\!\left({\frac {\omega }{2\pi }}\right)={\frac {1}{(2\pi )^{\frac {n}{2}}}}{\widehat {f_{3}}}(\omega )\\f(x)&={\frac {1}{(2\pi )^{\frac {n}{2}}}}\int _{\mathbb {R} ^{n}}{\widehat {f_{2}}}(\omega )e^{i\omega \cdot x}\,d\omega \end{aligned}}}$
	non-unitary	${\displaystyle {\begin{aligned}{\widehat {f_{3}}}(\omega )\ &\triangleq \ \int _{\mathbb {R} ^{n}}f(x)e^{-i\omega \cdot x}\,dx={\widehat {f_{1}}}\left({\frac {\omega }{2\pi }}\right)=(2\pi )^{\frac {n}{2}}{\widehat {f_{2}}}(\omega )\\f(x)&={\frac {1}{(2\pi )^{n}}}\int _{\mathbb {R} ^{n}}{\widehat {f_{3}}}(\omega )e^{i\omega \cdot x}\,d\omega \end{aligned}}}$

Extension of the definition[edit]

For ${\displaystyle 1<p<2}$, the Fourier transform can be defined on ${\displaystyle L^{p}(\mathbb {R} )}$ by Marcinkiewicz interpolation.

The Fourier transform can be defined on domains other than the real line. The Fourier transform on Euclidean space and the Fourier transform on locally abelian groups are discussed later in the article.

The Fourier transform can also be defined for tempered distributions, dual to the space of rapidly decreasing functions (Schwartz functions). A Schwartz function is a smooth function that decays at infinity, along with all of its derivatives. The space of Schwartz functions is denoted by ${\displaystyle {\mathcal {S}}(\mathbb {R} )}$, and its dual ${\displaystyle {\mathcal {S}}'(\mathbb {R} )}$ is the space of tempered distributions. It is easy to see, by differentiating under the integral and applying the Riemann-Lebesgue lemma, that the Fourier transform of a Schwartz function (defined by the formula Eq.1) is again a Schwartz function. The Fourier transform of a tempered distribution ${\displaystyle T\in {\mathcal {S}}'(\mathbb {R} )}$ is defined by duality:

${\displaystyle \langle {\widehat {T}},\phi \rangle =\langle T,{\widehat {\phi }}\rangle ;\quad \forall \phi \in {\mathcal {S}}(\mathbb {R} ).}$

Many other characterizations of the Fourier transform exist. For example, one uses the Stone–von Neumann theorem: the Fourier transform is the unique unitary intertwiner for the symplectic and Euclidean Schrödinger representations of the Heisenberg group.

Background[edit]

History[edit]

In 1822, Fourier claimed (see Joseph Fourier § The Analytic Theory of Heat) that any function, whether continuous or discontinuous, can be expanded into a series of sines.^[11] That important work was corrected and expanded upon by others to provide the foundation for the various forms of the Fourier transform used since.

Complex sinusoids[edit]

In general, the coefficients ${\displaystyle {\widehat {f}}(\xi )}$ are complex numbers, which have two equivalent forms (see Euler's formula):

${\displaystyle {\widehat {f}}(\xi )=\underbrace {Ae^{i\theta }} _{\text{polar coordinate form}}=\underbrace {A\cos(\theta )+iA\sin(\theta )} _{\text{rectangular coordinate form}}.}$

The product with ${\displaystyle e^{i2\pi \xi x}}$ (Eq.2) has these forms:

${\displaystyle {\widehat {f}}(\xi )\cdot e^{i2\pi \xi x}=Ae^{i\theta }\cdot e^{i2\pi \xi x}=\underbrace {Ae^{i(2\pi \xi x+\theta )}} _{\text{polar coordinate form}}=\underbrace {A\cos(2\pi \xi x+\theta )+iA\sin(2\pi \xi x+\theta )} _{\text{rectangular coordinate form}}.}$

It is noteworthy how easily the product was simplified using the polar form, and how easily the rectangular form was deduced by an application of Euler's formula.

Negative frequency[edit]

Euler's formula introduces the possibility of negative ${\displaystyle \xi .}$  And Eq.1 is defined ${\displaystyle \forall \xi \in \mathbb {R} .}$ Only certain complex-valued ${\displaystyle f(x)}$ have transforms ${\displaystyle {\widehat {f}}=0,\ \forall \ \xi <0}$ (See Analytic signal. A simple example is ${\displaystyle e^{i2\pi \xi _{0}x}\ (\xi _{0}>0).}$)  But negative frequency is necessary to characterize all other complex-valued ${\displaystyle f(x),}$ found in signal processing, partial differential equations, radar, nonlinear optics, quantum mechanics, and others.

For a real-valued ${\displaystyle f(x),}$ Eq.1 has the symmetry property ${\displaystyle {\widehat {f}}(-\xi )={\widehat {f}}^{*}(\xi )}$ (see § Conjugation below). This redundancy enables Eq.2 to distinguish ${\displaystyle f(x)=\cos(2\pi \xi _{0}x)}$ from ${\displaystyle e^{i2\pi \xi _{0}x}.}$  But of course it cannot tell us the actual sign of ${\displaystyle \xi _{0},}$ because ${\displaystyle \cos(2\pi \xi _{0}x)}$ and ${\displaystyle \cos(2\pi (-\xi _{0})x)}$ are indistinguishable on just the real numbers line..

Fourier transform for periodic functions[edit]

The Fourier transform of a periodic function cannot be defined using the integral formula directly. In order for integral in Eq.1 to be defined the function must be absolutely integrable. Instead it is common to use Fourier series. It is possible to extend the definition to include periodic functions by viewing them as tempered distributions.

This makes it possible to see a connection between the Fourier series and the Fourier transform for periodic functions that have a convergent Fourier series. If ${\displaystyle f(x)}$ is a periodic function, with period ${\displaystyle P}$, that has a convergent Fourier series, then:

${\displaystyle {\widehat {f}}(\xi )=\sum _{n=-\infty }^{\infty }c_{n}\cdot \delta \left(\xi -{\tfrac {n}{P}}\right),}$

where ${\displaystyle c_{n}}$ are the Fourier series coefficients of ${\displaystyle f}$, and ${\displaystyle \delta }$ is the Dirac delta function. In other words, the Fourier transform is a Dirac comb function whose teeth are multiplied by the Fourier series coefficients.

Sampling the Fourier transform[edit]

The Fourier transform of an integrable function ${\displaystyle f}$ can be sampled at regular intervals of arbitrary length ${\displaystyle {\tfrac {1}{P}}.}$ These samples can be deduced from one cycle of a periodic function ${\displaystyle f_{P}}$ which has Fourier series coefficients proportional to those samples by the Poisson summation formula:

${\displaystyle f_{P}(x)\triangleq \sum _{n=-\infty }^{\infty }f(x+nP)={\frac {1}{P}}\sum _{k=-\infty }^{\infty }{\widehat {f}}\left({\tfrac {k}{P}}\right)e^{i2\pi {\frac {k}{P}}x},\quad \forall k\in \mathbb {Z} }$

The integrability of ${\displaystyle f}$ ensures the periodic summation converges. Therefore, the samples ${\displaystyle {\widehat {f}}\left({\tfrac {k}{P}}\right)}$ can be determined by Fourier series analysis:

${\displaystyle {\widehat {f}}\left({\tfrac {k}{P}}\right)=\int _{P}f_{P}(x)\cdot e^{-i2\pi {\frac {k}{P}}x}\,dx.}$

When ${\displaystyle f(x)}$ has compact support, ${\displaystyle f_{P}(x)}$ has a finite number of terms within the interval of integration. When ${\displaystyle f(x)}$ does not have compact support, numerical evaluation of ${\displaystyle f_{P}(x)}$ requires an approximation, such as tapering ${\displaystyle f(x)}$ or truncating the number of terms.

Example[edit]

The following figures provide a visual illustration of how the Fourier transform measures whether a frequency is present in a particular function. The depicted function ${\displaystyle f(t)=\cos(2\pi \ 3t)\ e^{-\pi t^{2}}}$oscillates at 3 Hz (if ${\displaystyle t}$ measures seconds) and tends quickly to 0. (The second factor in this equation is an envelope function that shapes the continuous sinusoid into a short pulse.). ${\displaystyle f(t)}$ was specially chosen to have a real Fourier transform that can be easily plotted. The first image is its graph. In order to calculate ${\displaystyle {\widehat {f}}(3)}$ we must integrate the product ${\displaystyle f(t)e^{-i2\pi 3t}.}$ The next 2 images are the real and imaginary parts of that product. The real part of the integrand has a non-negative average value, because the alternating signs of ${\displaystyle f(t)}$ and ${\displaystyle \operatorname {Re} (e^{-i2\pi 3t})}$ oscillate at the same rate and same phase, whereas ${\displaystyle f(t)}$ and ${\displaystyle \operatorname {Im} (e^{-i2\pi 3t})}$ are same rate but orthogonal phase. The result is that when you integrate the real part of the integrand you get a relatively large number (in this case ${\displaystyle {\tfrac {1}{2}}}$). Also, when you try to measure a frequency that is not present, as in the case when we look at ${\displaystyle {\widehat {f}}(5),}$ both real and imaginary component of the product vary rapidly between positive and negative values. Therefore, the integral is very small and the value for the Fourier transform for that frequency is nearly zero. The general situation is usually more complicated than this, but heuristically this is how the Fourier transform measures how much of an individual frequency is present in a function ${\displaystyle \displaystyle f(t).}$

• 
  Real and imaginary parts of integrand for Fourier transform at 5 Hz
• 
  Magnitude of Fourier transform, with 3 and 5 Hz labeled.

To re-enforce an earlier point, the reason for the response at  ${\displaystyle \xi =-3}$ Hz  is because  ${\displaystyle \cos(2\pi 3t)}$  and  ${\displaystyle \cos(2\pi (-3)t)}$  are indistinguishable. The transform of  ${\displaystyle e^{i2\pi 3t}\cdot e^{-\pi t^{2}}}$  would have just one response, whose amplitude is the integral of the smooth envelope: ${\displaystyle e^{-\pi t^{2}},}$  whereas  ${\displaystyle \operatorname {Re} (f(t)\cdot e^{-i2\pi 3t})}$ (second graph above) is  ${\displaystyle e^{-\pi t^{2}}(1+\cos(2\pi 6t))/2.}$

Properties of the Fourier transform[edit]

Let ${\displaystyle f(x)}$ and ${\displaystyle h(x)}$ represent integrable functions Lebesgue-measurable on the real line satisfying:

${\displaystyle \int _{-\infty }^{\infty }|f(x)|\,dx<\infty .}$

We denote the Fourier transforms of these functions as ${\displaystyle {\hat {f}}(\xi )}$ and ${\displaystyle {\hat {h}}(\xi )}$ respectively.

Basic properties[edit]

The Fourier transform has the following basic properties:^[12]

Linearity[edit]

${\displaystyle a\ f(x)+b\ h(x)\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ a\ {\widehat {f}}(\xi )+b\ {\widehat {h}}(\xi );\quad \ a,b\in \mathbb {C} }$

Time shifting[edit]

${\displaystyle f(x-x_{0})\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ e^{-i2\pi x_{0}\xi }\ {\widehat {f}}(\xi );\quad \ x_{0}\in \mathbb {R} }$

Frequency shifting[edit]

${\displaystyle e^{i2\pi \xi _{0}x}f(x)\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\widehat {f}}(\xi -\xi _{0});\quad \ \xi _{0}\in \mathbb {R} }$

Time scaling[edit]

${\displaystyle f(ax)\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\frac {1}{|a|}}{\widehat {f}}\left({\frac {\xi }{a}}\right);\quad \ a\neq 0}$

The case ${\displaystyle a=-1}$ leads to the time-reversal property:

${\displaystyle f(-x)\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\widehat {f}}(-\xi )}$

Symmetry[edit]

When the real and imaginary parts of a complex function are decomposed into their even and odd parts, there are four components, denoted below by the subscripts RE, RO, IE, and IO. And there is a one-to-one mapping between the four components of a complex time function and the four components of its complex frequency transform:

$${\displaystyle {\begin{aligned}{\mathsf {Time\ domain}}\quad &\ f\quad &=\quad &f_{_{RE}}\quad &+\quad &f_{_{RO}}\quad &+\quad i\ &f_{_{IE}}\quad &+\quad &\underbrace {i\ f_{_{IO}}} \\&{\Bigg \Updownarrow }{\mathcal {F}}&&{\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}\\{\mathsf {Frequency\ domain}}\quad &{\widehat {f}}\quad &=\quad &{\widehat {f}}_{RE}\quad &+\quad &\overbrace {i\ {\widehat {f}}_{IO}} \quad &+\quad i\ &{\widehat {f}}_{IE}\quad &+\quad &{\widehat {f}}_{RO}\end{aligned}}}$$

From this, various relationships are apparent, for example:

• The transform of a real-valued function (f_RE+ f_RO) is the even symmetric function f̂_RE+ i f̂_IO. Conversely, an even-symmetric transform implies a real-valued time-domain.
• The transform of an imaginary-valued function (i f_IE+ i f_IO) is the odd symmetric function f̂_RO+ i f̂_IE, and the converse is true.
• The transform of an even-symmetric function (f_RE+ i f_IO) is the real-valued function f̂_RE+ f̂_RO, and the converse is true.
• The transform of an odd-symmetric function (f_RO+ i f_IE) is the imaginary-valued function i f̂_IE+ i f̂_IO, and the converse is true.

Conjugation[edit]

${\displaystyle {\bigl (}f(x){\bigr )}^{*}\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ \left({\widehat {f}}(-\xi )\right)^{*}}$

(Note: the ∗ denotes complex conjugation.)

In particular, if ${\displaystyle f}$ is real, then ${\displaystyle {\widehat {f}}}$ is even symmetric (aka Hermitian function):

${\displaystyle {\widehat {f}}(-\xi )={\bigl (}{\widehat {f}}(\xi ){\bigr )}^{*}.}$

And if ${\displaystyle f}$ is purely imaginary, then ${\displaystyle {\widehat {f}}}$ is odd symmetric:

${\displaystyle {\widehat {f}}(-\xi )=-({\widehat {f}}(\xi ))^{*}.}$

Real and imaginary part in time[edit]

${\displaystyle \operatorname {Re} \{f(x)\}\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\tfrac {1}{2}}\left({\widehat {f}}(\xi )+{\bigl (}{\widehat {f}}(-\xi ){\bigr )}^{*}\right)}$

${\displaystyle \operatorname {Im} \{f(x)\}\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\tfrac {1}{2i}}\left({\widehat {f}}(\xi )-{\bigl (}{\widehat {f}}(-\xi ){\bigr )}^{*}\right)}$

The zero frequency component[edit]

Substituting ${\displaystyle \xi =0}$ in the definition, we obtain:

${\displaystyle {\widehat {f}}(0)=\int _{-\infty }^{\infty }f(x)\,dx.}$

The integral of ${\displaystyle f}$ over its domain is known as the average value or DC bias of the function.

Invertibility and periodicity[edit]

Under suitable conditions on the function ${\displaystyle f}$, it can be recovered from its Fourier transform ${\displaystyle {\hat {f}}}$. Indeed, denoting the Fourier transform operator by ${\displaystyle {\mathcal {F}}}$, so ${\displaystyle {\mathcal {F}}f:={\hat {f}}}$, then for suitable functions, applying the Fourier transform twice simply flips the function: ${\displaystyle \left({\mathcal {F}}^{2}f\right)(x)=f(-x)}$, which can be interpreted as "reversing time". Since reversing time is two-periodic, applying this twice yields ${\displaystyle {\mathcal {F}}^{4}(f)=f}$, so the Fourier transform operator is four-periodic, and similarly the inverse Fourier transform can be obtained by applying the Fourier transform three times: ${\displaystyle {\mathcal {F}}^{3}\left({\hat {f}}\right)=f}$. In particular the Fourier transform is invertible (under suitable conditions).

More precisely, defining the parity operator ${\displaystyle {\mathcal {P}}}$ such that ${\displaystyle ({\mathcal {P}}f)(x)=f(-x)}$, we have:

${\displaystyle {\begin{aligned}{\mathcal {F}}^{0}&=\mathrm {id} ,\\{\mathcal {F}}^{1}&={\mathcal {F}},\\{\mathcal {F}}^{2}&={\mathcal {P}},\\{\mathcal {F}}^{3}&={\mathcal {F}}^{-1}={\mathcal {P}}\circ {\mathcal {F}}={\mathcal {F}}\circ {\mathcal {P}},\\{\mathcal {F}}^{4}&=\mathrm {id} \end{aligned}}}$

These equalities of operators require careful definition of the space of functions in question, defining equality of functions (equality at every point? equality almost everywhere?) and defining equality of operators – that is, defining the topology on the function space and operator space in question. These are not true for all functions, but are true under various conditions, which are the content of the various forms of the Fourier inversion theorem.

This fourfold periodicity of the Fourier transform is similar to a rotation of the plane by 90°, particularly as the two-fold iteration yields a reversal, and in fact this analogy can be made precise. While the Fourier transform can simply be interpreted as switching the time domain and the frequency domain, with the inverse Fourier transform switching them back, more geometrically it can be interpreted as a rotation by 90° in the time–frequency domain (considering time as the x-axis and frequency as the y-axis), and the Fourier transform can be generalized to the fractional Fourier transform, which involves rotations by other angles. This can be further generalized to linear canonical transformations, which can be visualized as the action of the special linear group SL₂(R) on the time–frequency plane, with the preserved symplectic form corresponding to the uncertainty principle, below. This approach is particularly studied in signal processing, under time–frequency analysis.

Units[edit]

The frequency variable must have inverse units to the units of the original function's domain (typically named t or x). For example, if t is measured in seconds, ξ should be in cycles per second or hertz. If the scale of time is in units of 2π seconds, then another Greek letter ω typically is used instead to represent angular frequency (where ω = 2πξ) in units of radians per second. If using x for units of length, then ξ must be in inverse length, e.g., wavenumbers. That is to say, there are two versions of the real line: one which is the range of t and measured in units of t, and the other which is the range of ξ and measured in inverse units to the units of t. These two distinct versions of the real line cannot be equated with each other. Therefore, the Fourier transform goes from one space of functions to a different space of functions: functions which have a different domain of definition.

In general, ξ must always be taken to be a linear form on the space of its domain, which is to say that the second real line is the dual space of the first real line. See the article on linear algebra for a more formal explanation and for more details. This point of view becomes essential in generalizations of the Fourier transform to general symmetry groups, including the case of Fourier series.

That there is no one preferred way (often, one says "no canonical way") to compare the two versions of the real line which are involved in the Fourier transform—fixing the units on one line does not force the scale of the units on the other line—is the reason for the plethora of rival conventions on the definition of the Fourier transform. The various definitions resulting from different choices of units differ by various constants.

In other conventions, the Fourier transform has i in the exponent instead of −i, and vice versa for the inversion formula. This convention is common in modern physics^[13] and is the default for Wolfram Alpha, and does not mean that the frequency has become negative, since there is no canonical definition of positivity for frequency of a complex wave. It simply means that ${\displaystyle {\hat {f}}(\xi )}$ is the amplitude of the wave  ${\displaystyle e^{-i2\pi \xi x}}$  instead of the wave  ${\displaystyle e^{i2\pi \xi x}}$ (the former, with its minus sign, is often seen in the time dependence for Sinusoidal plane-wave solutions of the electromagnetic wave equation, or in the time dependence for quantum wave functions). Many of the identities involving the Fourier transform remain valid in those conventions, provided all terms that explicitly involve i have it replaced by −i. In Electrical engineering the letter j is typically used for the imaginary unit instead of i because i is used for current.

When using dimensionless units, the constant factors might not even be written in the transform definition. For instance, in probability theory, the characteristic function Φ of the probability density function f of a random variable X of continuous type is defined without a negative sign in the exponential, and since the units of x are ignored, there is no 2π either:

${\displaystyle \phi (\lambda )=\int _{-\infty }^{\infty }f(x)e^{i\lambda x}\,dx.}$

(In probability theory, and in mathematical statistics, the use of the Fourier—Stieltjes transform is preferred, because so many random variables are not of continuous type, and do not possess a density function, and one must treat not functions but distributions, i.e., measures which possess "atoms".)

From the higher point of view of group characters, which is much more abstract, all these arbitrary choices disappear, as will be explained in the later section of this article, which treats the notion of the Fourier transform of a function on a locally compact Abelian group.

Uniform continuity and the Riemann–Lebesgue lemma[edit]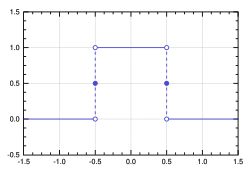

The Fourier transform may be defined in some cases for non-integrable functions, but the Fourier transforms of integrable functions have several strong properties.

The Fourier transform f̂ of any integrable function f is uniformly continuous and^[14]

${\displaystyle \left\|{\hat {f}}\right\|_{\infty }\leq \left\|f\right\|_{1}}$

By the Riemann–Lebesgue lemma,^[15]

${\displaystyle {\hat {f}}(\xi )\to 0{\text{ as }}|\xi |\to \infty .}$

However, ${\displaystyle {\hat {f}}}$ need not be integrable. For example, the Fourier transform of the rectangular function, which is integrable, is the sinc function, which is not Lebesgue integrable, because its improper integrals behave analogously to the alternating harmonic series, in converging to a sum without being absolutely convergent.

It is not generally possible to write the inverse transform as a Lebesgue integral. However, when both f and ${\displaystyle {\hat {f}}}$ are integrable, the inverse equality

${\displaystyle f(x)=\int _{-\infty }^{\infty }{\hat {f}}(\xi )e^{i2\pi x\xi }\,d\xi }$

holds holds for almost every x. As a result, the Fourier transform is injective on L¹(R).

Plancherel theorem and Parseval's theorem[edit]

Let f(x) and g(x) be integrable, and let f̂(ξ) and ĝ(ξ) be their Fourier transforms. If f(x) and g(x) are also square-integrable, then the Parseval formula follows:^[16]

${\displaystyle \langle f,g\rangle _{L^{2}}=\int _{-\infty }^{\infty }f(x){\overline {g(x)}}\,dx=\int _{-\infty }^{\infty }{\hat {f}}(\xi ){\overline {{\hat {g}}(\xi )}}\,d\xi ,}$

where the bar denotes complex conjugation.

The Plancherel theorem, which follows from the above, states that^[17]

${\displaystyle \|f\|_{L^{2}}^{2}=\int _{-\infty }^{\infty }\left|f(x)\right|^{2}\,dx=\int _{-\infty }^{\infty }\left|{\hat {f}}(\xi )\right|^{2}\,d\xi .}$

Plancherel's theorem makes it possible to extend the Fourier transform, by a continuity argument, to a unitary operator on L²(R). On L¹(R) ∩ L²(R), this extension agrees with original Fourier transform defined on L¹(R), thus enlarging the domain of the Fourier transform to L¹(R) + L²(R) (and consequently to L^p(R) for 1 ≤ p ≤ 2). Plancherel's theorem has the interpretation in the sciences that the Fourier transform preserves the energy of the original quantity. The terminology of these formulas is not quite standardised. Parseval's theorem was proved only for Fourier series, and was first proved by Lyapunov. But Parseval's formula makes sense for the Fourier transform as well, and so even though in the context of the Fourier transform it was proved by Plancherel, it is still often referred to as Parseval's formula, or Parseval's relation, or even Parseval's theorem.

See Pontryagin duality for a general formulation of this concept in the context of locally compact abelian groups.

Poisson summation formula[edit]

The Poisson summation formula (PSF) is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. The Poisson summation formula says that for sufficiently regular functions f,

${\displaystyle \sum _{n}{\hat {f}}(n)=\sum _{n}f(n).}$

It has a variety of useful forms that are derived from the basic one by application of the Fourier transform's scaling and time-shifting properties. The formula has applications in engineering, physics, and number theory. The frequency-domain dual of the standard Poisson summation formula is also called the discrete-time Fourier transform.

Poisson summation is generally associated with the physics of periodic media, such as heat conduction on a circle. The fundamental solution of the heat equation on a circle is called a theta function. It is used in number theory to prove the transformation properties of theta functions, which turn out to be a type of modular form, and it is connected more generally to the theory of automorphic forms where it appears on one side of the Selberg trace formula.

Differentiation[edit]

Suppose f(x) is an absolutely continuous differentiable function, and both f and its derivative f′ are integrable. Then the Fourier transform of the derivative is given by

${\displaystyle {\widehat {f'\,}}(\xi )={\mathcal {F}}\left\{{\frac {d}{dx}}f(x)\right\}=i2\pi \xi {\hat {f}}(\xi ).}$

More generally, the Fourier transformation of the nth derivative f⁽ⁿ⁾ is given by

${\displaystyle {\widehat {f^{(n)}}}(\xi )={\mathcal {F}}\left\{{\frac {d^{n}}{dx^{n}}}f(x)\right\}=(i2\pi \xi )^{n}{\hat {f}}(\xi ).}$

Analogically, ${\displaystyle {\mathcal {F}}\left\{{\frac {d^{n}}{d\xi ^{n}}}{\hat {f}}(\xi )\right\}=(i2\pi x)^{n}f(x)}$, so ${\displaystyle {\mathcal {F}}\left\{x^{n}f(x)\right\}=\left({\frac {i}{2\pi }}\right)^{n}{\frac {d^{n}}{d\xi ^{n}}}{\hat {f}}(\xi ).}$

By applying the Fourier transform and using these formulas, some ordinary differential equations can be transformed into algebraic equations, which are much easier to solve. These formulas also give rise to the rule of thumb "f(x) is smooth if and only if f̂(ξ) quickly falls to 0 for |ξ| → ∞." By using the analogous rules for the inverse Fourier transform, one can also say "f(x) quickly falls to 0 for |x| → ∞ if and only if f̂(ξ) is smooth."

Convolution theorem[edit]

The Fourier transform translates between convolution and multiplication of functions. If f(x) and g(x) are integrable functions with Fourier transforms f̂(ξ) and ĝ(ξ) respectively, then the Fourier transform of the convolution is given by the product of the Fourier transforms f̂(ξ) and ĝ(ξ) (under other conventions for the definition of the Fourier transform a constant factor may appear).

This means that if:

${\displaystyle h(x)=(f*g)(x)=\int _{-\infty }^{\infty }f(y)g(x-y)\,dy,}$

where ∗ denotes the convolution operation, then:

${\displaystyle {\hat {h}}(\xi )={\hat {f}}(\xi )\,{\hat {g}}(\xi ).}$

In linear time invariant (LTI) system theory, it is common to interpret g(x) as the impulse response of an LTI system with input f(x) and output h(x), since substituting the unit impulse for f(x) yields h(x) = g(x). In this case, ĝ(ξ) represents the frequency response of the system.

Conversely, if f(x) can be decomposed as the product of two square integrable functions p(x) and q(x), then the Fourier transform of f(x) is given by the convolution of the respective Fourier transforms p̂(ξ) and q̂(ξ).

Cross-correlation theorem[edit]

In an analogous manner, it can be shown that if h(x) is the cross-correlation of f(x) and g(x):

${\displaystyle h(x)=(f\star g)(x)=\int _{-\infty }^{\infty }{\overline {f(y)}}g(x+y)\,dy}$

then the Fourier transform of h(x) is:

${\displaystyle {\hat {h}}(\xi )={\overline {{\hat {f}}(\xi )}}\,{\hat {g}}(\xi ).}$

As a special case, the autocorrelation of function f(x) is:

${\displaystyle h(x)=(f\star f)(x)=\int _{-\infty }^{\infty }{\overline {f(y)}}f(x+y)\,dy}$

for which

${\displaystyle {\hat {h}}(\xi )={\overline {{\hat {f}}(\xi )}}{\hat {f}}(\xi )=\left|{\hat {f}}(\xi )\right|^{2}.}$

Eigenfunctions[edit]

The Fourier transform is a linear transform which has eigenfunctions obeying ${\displaystyle {\mathcal {F}}[\psi ]=\lambda \psi ,}$ with ${\displaystyle \lambda \in \mathbb {C} .}$

A set of eigenfunctions is found by noting that the homogeneous differential equation

${\displaystyle \left[U\left({\frac {1}{2\pi }}{\frac {d}{dx}}\right)+U(x)\right]\psi (x)=0}$

leads to eigenfunctions ${\displaystyle \psi (x)}$ of the Fourier transform ${\displaystyle {\mathcal {F}}}$ as long as the form of the equation remains invariant under Fourier transform.^{[note 6]} In other words, every solution ${\displaystyle \psi (x)}$ and its Fourier transform ${\displaystyle {\hat {\psi }}(\xi )}$ obey the same equation. Assuming uniqueness of the solutions, every solution ${\displaystyle \psi (x)}$ must therefore be an eigenfunction of the Fourier transform. The form of the equation remains unchanged under Fourier transform if ${\displaystyle U(x)}$ can be expanded in a power series in which for all terms the same factor of either one of ${\displaystyle \pm 1,\pm i}$ arises from the factors ${\displaystyle i^{n}}$ introduced by the differentiation rules upon Fourier transforming the homogeneous differential equation because this factor may then be cancelled. The simplest allowable ${\displaystyle U(x)=x}$ leads to the standard normal distribution.^[18]

More generally, a set of eigenfunctions is also found by noting that the differentiation rules imply that the ordinary differential equation

${\displaystyle \left[W\left({\frac {i}{2\pi }}{\frac {d}{dx}}\right)+W(x)\right]\psi (x)=C\psi (x)}$

with ${\displaystyle C}$ constant and ${\displaystyle W(x)}$ being a non-constant even function remains invariant in form when applying the Fourier transform ${\displaystyle {\mathcal {F}}}$ to both sides of the equation. The simplest example is provided by ${\displaystyle W(x)=x^{2}}$ which is equivalent to considering the Schrödinger equation for the quantum harmonic oscillator.^[19] The corresponding solutions provide an important choice of an orthonormal basis for L²(R) and are given by the "physicist's" Hermite functions. Equivalently one may use

${\displaystyle \psi _{n}(x)={\frac {\sqrt[{4}]{2}}{\sqrt {n!}}}e^{-\pi x^{2}}\mathrm {He} _{n}\left(2x{\sqrt {\pi }}\right),}$

where He_n(x) are the "probabilist's" Hermite polynomials, defined as

${\displaystyle \mathrm {He} _{n}(x)=(-1)^{n}e^{{\frac {1}{2}}x^{2}}\left({\frac {d}{dx}}\right)^{n}e^{-{\frac {1}{2}}x^{2}}.}$

Under this convention for the Fourier transform, we have that

${\displaystyle {\hat {\psi }}_{n}(\xi )=(-i)^{n}\psi _{n}(\xi ).}$

In other words, the Hermite functions form a complete orthonormal system of eigenfunctions for the Fourier transform on L²(R).^[12][20] However, this choice of eigenfunctions is not unique. Because of ${\displaystyle {\mathcal {F}}^{4}=\mathrm {id} }$ there are only four different eigenvalues of the Fourier transform (the fourth roots of unity ±1 and ±i) and any linear combination of eigenfunctions with the same eigenvalue gives another eigenfunction.^[21] As a consequence of this, it is possible to decompose L²(R) as a direct sum of four spaces H₀, H₁, H₂, and H₃ where the Fourier transform acts on He_k simply by multiplication by i^k.

Since the complete set of Hermite functions ψ_n provides a resolution of the identity they diagonalize the Fourier operator, i.e. the Fourier transform can be represented by such a sum of terms weighted by the above eigenvalues, and these sums can be explicitly summed:

${\displaystyle {\mathcal {F}}[f](\xi )=\int dxf(x)\sum _{n\geq 0}(-i)^{n}\psi _{n}(x)\psi _{n}(\xi )~.}$

This approach to define the Fourier transform was first proposed by Norbert Wiener.^[22] Among other properties, Hermite functions decrease exponentially fast in both frequency and time domains, and they are thus used to define a generalization of the Fourier transform, namely the fractional Fourier transform used in time–frequency analysis.^[23] In physics, this transform was introduced by Edward Condon.^[24] This change of basis functions becomes possible because the Fourier transform is a unitary transform when using the right conventions. Consequently, under the proper conditions it may be expected to result from a self-adjoint generator ${\displaystyle N}$ via^[25]

${\displaystyle {\mathcal {F}}[\psi ]=e^{-itN}\psi .}$

The operator ${\displaystyle N}$ is the number operator of the quantum harmonic oscillator written as^[26][27]

${\displaystyle N\equiv {\frac {1}{2}}\left(x-{\frac {\partial }{\partial x}}\right)\left(x+{\frac {\partial }{\partial x}}\right)={\frac {1}{2}}\left(-{\frac {\partial ^{2}}{\partial x^{2}}}+x^{2}-1\right).}$

It can be interpreted as the generator of fractional Fourier transforms for arbitrary values of t, and of the conventional continuous Fourier transform ${\displaystyle {\mathcal {F}}}$ for the particular value ${\displaystyle t=\pi /2,}$ with the Mehler kernel implementing the corresponding active transform. The eigenfunctions of ${\displaystyle N}$ are the Hermite functions ${\displaystyle \psi _{n}(x)}$ which are therefore also eigenfunctions of ${\displaystyle {\mathcal {F}}.}$

Upon extending the Fourier transform to distributions the Dirac comb is also an eigenfunction of the Fourier transform.

Connection with the Heisenberg group[edit]

The Heisenberg group is a certain group of unitary operators on the Hilbert space L²(R) of square integrable complex valued functions f on the real line, generated by the translations (T_y f)(x) = f (x + y) and multiplication by e^i2πξx, (M_ξ f)(x) = e^i2πξx f (x). These operators do not commute, as their (group) commutator is

$${\displaystyle \left(M_{\xi }^{-1}T_{y}^{-1}M_{\xi }T_{y}f\right)(x)=e^{i2\pi \xi y}f(x)}$$

$${\displaystyle \left(x_{1},\xi _{1},t_{1}\right)\cdot \left(x_{2},\xi _{2},t_{2}\right)=\left(x_{1}+x_{2},\xi _{1}+\xi _{2},t_{1}t_{2}e^{i2\pi \left(x_{1}\xi _{1}+x_{2}\xi _{2}+x_{1}\xi _{2}\right)}\right).}$$

Denote the Heisenberg group by H₁. The above procedure describes not only the group structure, but also a standard unitary representation of H₁ on a Hilbert space, which we denote by ρ : H₁ → B(L²(R)). Define the linear automorphism of R² by

$${\displaystyle J{\begin{pmatrix}x\\\xi \end{pmatrix}}={\begin{pmatrix}-\xi \\x\end{pmatrix}}}$$

so that J² = −I. This J can be extended to a unique automorphism of H₁:

$${\displaystyle j\left(x,\xi ,t\right)=\left(-\xi ,x,te^{-i2\pi \xi x}\right).}$$

According to the Stone–von Neumann theorem, the unitary representations ρ and ρ ∘ j are unitarily equivalent, so there is a unique intertwiner W ∈ U(L²(R)) such that

$${\displaystyle \rho \circ j=W\rho W^{*}.}$$

Many of the standard properties of the Fourier transform are immediate consequences of this more general framework.^[28] For example, the square of the Fourier transform, W², is an intertwiner associated with J² = −I, and so we have (W²f)(x) = f (−x) is the reflection of the original function f.

Complex domain[edit]

The integral for the Fourier transform

${\displaystyle {\hat {f}}(\xi )=\int _{-\infty }^{\infty }e^{-i2\pi \xi t}f(t)\,dt}$

can be studied for complex values of its argument ξ. Depending on the properties of f, this might not converge off the real axis at all, or it might converge to a complex analytic function for all values of ξ = σ + iτ, or something in between.^[29]

The Paley–Wiener theorem says that f is smooth (i.e., n-times differentiable for all positive integers n) and compactly supported if and only if f̂ (σ + iτ) is a holomorphic function for which there exists a constant a > 0 such that for any integer n ≥ 0,

${\displaystyle \left\vert \xi ^{n}{\hat {f}}(\xi )\right\vert \leq Ce^{a\vert \tau \vert }}$

for some constant C. (In this case, f is supported on [−a, a].) This can be expressed by saying that f̂ is an entire function which is rapidly decreasing in σ (for fixed τ) and of exponential growth in τ (uniformly in σ).^[30]

(If f is not smooth, but only L², the statement still holds provided n = 0.^[31]) The space of such functions of a complex variable is called the Paley—Wiener space. This theorem has been generalised to semisimple Lie groups.^[32]

If f is supported on the half-line t ≥ 0, then f is said to be "causal" because the impulse response function of a physically realisable filter must have this property, as no effect can precede its cause. Paley and Wiener showed that then f̂ extends to a holomorphic function on the complex lower half-plane τ < 0 which tends to zero as τ goes to infinity.^[33] The converse is false and it is not known how to characterise the Fourier transform of a causal function.^[34]