Ikeda map

This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (June 2016) (Learn how and when to remove this template message)

In physics and mathematics, the Ikeda map is a discrete-time dynamical system given by the complex map

$${\displaystyle z_{n+1}=A+Bz_{n}e^{i(|z_{n}|^{2}+C)}}$$

The original map was proposed first by Kensuke Ikeda as a model of light going around across a nonlinear optical resonator (ring cavity containing a nonlinear^{[disambiguation needed]} dielectric medium) in a more general form. It is reduced to the above simplified "normal" form by Ikeda, Daido and Akimoto ^[1][2] ${\displaystyle z_{n}}$ stands for the electric field inside the resonator at the n-th step of rotation in the resonator, and ${\displaystyle A}$ and ${\displaystyle C}$ are parameters which indicate laser light applied from the outside, and linear phase across the resonator, respectively. In particular the parameter ${\displaystyle B\leq 1}$ is called dissipation parameter characterizing the loss of resonator, and in the limit of ${\displaystyle B=1}$ the Ikeda map becomes a conservative map.

The original Ikeda map is often used in another modified form in order to take the saturation effect of nonlinear dielectric medium into account:

$${\displaystyle z_{n+1}=A+Bz_{n}e^{iK/(|z_{n}|^{2}+1)+C}}$$

A 2D real example of the above form is:

$${\displaystyle x_{n+1}=1+u(x_{n}\cos t_{n}-y_{n}\sin t_{n}),\,}$$

$${\displaystyle y_{n+1}=u(x_{n}\sin t_{n}+y_{n}\cos t_{n}),}$$

$${\displaystyle t_{n}=0.4-{\frac {6}{1+x_{n}^{2}+y_{n}^{2}}}.}$$

For ${\displaystyle u\geq 0.6}$, this system has a chaotic attractor.

Attractor[edit]

This animation shows how the attractor of the system changes as the parameter ${\displaystyle u}$ is varied from 0.0 to 1.0 in steps of 0.01. The Ikeda dynamical system is simulated for 500 steps, starting from 20000 randomly placed starting points. The last 20 points of each trajectory are plotted to depict the attractor. Note the bifurcation of attractor points as ${\displaystyle u}$ is increased.

Point trajectories[edit]

The plots below show trajectories of 200 random points for various values of ${\displaystyle u}$. The inset plot on the left shows an estimate of the attractor while the inset on the right shows a zoomed in view of the main trajectory plot.

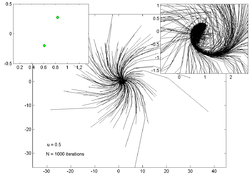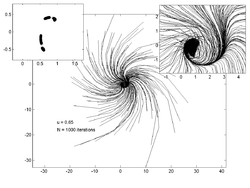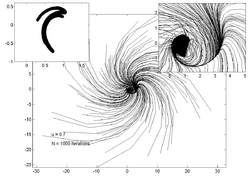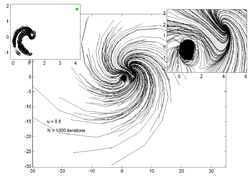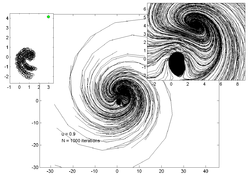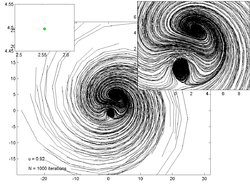Octave/MATLAB code for point trajectories[edit]

The Octave/MATLAB code to generate these plots is given below:

% u = ikeda parameter % option = what to plot %  'trajectory' - plot trajectory of random starting points %  'limit' - plot the last few iterations of random starting points function ikeda(u, option) P = 200; % how many starting points N = 1000; % how many iterations Nlimit = 20; % plot these many last points for 'limit' option   x = randn(1, P) * 10; % the random starting points y = randn(1, P) * 10;   for n = 1:P,     X = compute_ikeda_trajectory(u, x(n), y(n), N);           switch option         case 'trajectory' % plot the trajectories of a bunch of points             plot_ikeda_trajectory(X); hold on;          case 'limit'             plot_limit(X, Nlimit); hold on;          otherwise             disp('Not implemented');     end end  axis tight; axis equal text(- 25, - 15, ['u = ' num2str(u)]); text(- 25, - 18, ['N = ' num2str(N) ' iterations']); end  % Plot the last n points of the curve - to see end point or limit cycle function plot_limit(X, n) plot(X(end - n:end, 1), X(end - n:end, 2), 'ko'); end  % Plot the whole trajectory function plot_ikeda_trajectory(X) plot(X(:, 1), X(:, 2), 'k'); % hold on; plot(X(1,1), X(1,2), 'bo', 'markerfacecolor', 'g'); hold off end  % u is the ikeda parameter % x,y is the starting point % N is the number of iterations function [X] = compute_ikeda_trajectory(u, x, y, N) X = zeros(N, 2); X(1, :) = [x y];   for n = 2:N           t = 0.4 - 6 / (1 + x ^ 2 + y ^ 2);     x1 = 1 + u * (x * cos(t) - y * sin(t));     y1 = u * (x * sin(t) + y * cos(t));     x = x1;     y = y1;      X(n, :) = [x y]; end end 

Python code for point trajectories[edit]

import math  import matplotlib.pyplot as plt import numpy as np  def main(u: float, points=200, iterations=1000, nlim=20, limit=False, title=True):     """     Args:         u:float             ikeda parameter         points:int             number of starting points         iterations:int             number of iterations         nlim:int             plot these many last points for 'limit' option. Will plot all points if set to zero         limit:bool             plot the last few iterations of random starting points if True. Else Plot trajectories.         title:[str, NoneType]             display the name of the plot if the value is affirmative     """          x = 10 * np.random.randn(points, 1)     y = 10 * np.random.randn(points, 1)          for n in range(points):         X = compute_ikeda_trajectory(u, x[n][0], y[n][0], iterations)                  if limit:             plot_limit(X, nlim)             tx, ty = 2.5, -1.8                      else:             plot_ikeda_trajectory(X)             tx, ty = -30, -26          plt.title(f"Ikeda Map ({u=:.2g}, {iterations=})") if title else None     return plt  def compute_ikeda_trajectory(u: float, x: float, y: float, N: int):     """Calculate a full trajectory      Args:         u - is the ikeda parameter         x, y - coordinates of the starting point         N - the number of iterations      Returns:         An array.     """     X = np.zeros((N, 2))          for n in range(N):         X[n] = np.array((x, y))                  t = 0.4 - 6 / (1 + x ** 2 + y ** 2)         x1 = 1 + u * (x * math.cos(t) - y * math.sin(t))         y1 = u * (x * math.sin(t) + y * math.cos(t))                  x = x1         y = y1                 return X  def plot_limit(X, n: int) -> None:     """     Plot the last n points of the curve - to see end point or limit cycle      Args:         X: np.array             trajectory of an associated starting-point         n: int             number of "last" points to plot     """     plt.plot(X[-n:, 0], X[-n:, 1], 'ko')  def plot_ikeda_trajectory(X) -> None:     """     Plot the whole trajectory      Args:         X: np.array             trajectory of an associated starting-point     """     plt.plot(X[:,0], X[:, 1], "k")  if __name__ == "__main__":     main(0.9, limit=True, nlim=0).show() 

References[edit]