The kappa curve has two vertical asymptotes In geometry , the kappa curve or Gutschoven's curve is a two-dimensional algebraic curve resembling the Greek letter ϰ (kappa)Gérard van Gutschoven around 1662. In the history of mathematics , it is remembered as one of the first examples of Isaac Barrow 's application of rudimentary calculus methods to determine the tangent of a curve. Isaac Newton and Johann Bernoulli continued the studies of this curve subsequently.
Using the Cartesian coordinate system it can be expressed as
x 2 ( x 2 + y 2 ) = a 2 y 2 {\displaystyle x^{2}\left(x^{2}+y^{2}\right)=a^{2}y^{2}} or, using parametric equations ,
x = a sin t , y = a sin t tan t . {\displaystyle {\begin{aligned}x&=a\sin t,\\y&=a\sin t\tan t.\end{aligned}}} In polar coordinates its equation is even simpler:
r = a tan θ . {\displaystyle r=a\tan \theta .} It has two vertical asymptotes at x = ±a
The kappa curve's curvature :
κ ( θ ) = 8 ( 3 − sin 2 θ ) sin 4 θ a ( sin 2 ( 2 θ ) + 4 ) 3 2 . {\displaystyle \kappa (\theta )={\frac {8\left(3-\sin ^{2}\theta \right)\sin ^{4}\theta }{a\left(\sin ^{2}(2\theta )+4\right)^{\frac {3}{2}}}}.} Tangential angle:
ϕ ( θ ) = − arctan ( 1 2 sin ( 2 θ ) ) . {\displaystyle \phi (\theta )=-\arctan \left({\tfrac {1}{2}}\sin(2\theta )\right).} Tangents via infinitesimals [ edit ] The tangent lines of the kappa curve can also be determined geometrically using differentials and the elementary rules of infinitesimal arithmetic. Suppose x and y are variables, while a is taken to be a constant. From the definition of the kappa curve,
x 2 ( x 2 + y 2 ) − a 2 y 2 = 0 {\displaystyle x^{2}\left(x^{2}+y^{2}\right)-a^{2}y^{2}=0} Now, an infinitesimal change in our location must also change the value of the left hand side, so
d ( x 2 ( x 2 + y 2 ) − a 2 y 2 ) = 0 {\displaystyle d\left(x^{2}\left(x^{2}+y^{2}\right)-a^{2}y^{2}\right)=0} Distributing the differential and applying appropriate rules ,
d ( x 2 ( x 2 + y 2 ) ) − d ( a 2 y 2 ) = 0 ( 2 x d x ) ( x 2 + y 2 ) + x 2 ( 2 x d x + 2 y d y ) − a 2 2 y d y = 0 ( 4 x 3 + 2 x y 2 ) d x + ( 2 y x 2 − 2 a 2 y ) d y = 0 x ( 2 x 2 + y 2 ) d x + y ( x 2 − a 2 ) d y = 0 x ( 2 x 2 + y 2 ) y ( a 2 − x 2 ) = d y d x {\displaystyle {\begin{aligned}d\left(x^{2}\left(x^{2}+y^{2}\right)\right)-d\left(a^{2}y^{2}\right)&=0\\[6px](2x\,dx)\left(x^{2}+y^{2}\right)+x^{2}(2x\,dx+2y\,dy)-a^{2}2y\,dy&=0\\[6px]\left(4x^{3}+2xy^{2}\right)dx+\left(2yx^{2}-2a^{2}y\right)dy&=0\\[6px]x\left(2x^{2}+y^{2}\right)dx+y\left(x^{2}-a^{2}\right)dy&=0\\[6px]{\frac {x\left(2x^{2}+y^{2}\right)}{y\left(a^{2}-x^{2}\right)}}&={\frac {dy}{dx}}\end{aligned}}} If we use the modern concept of a functional relationship y (x )implicit differentiation , the slope of a tangent line to the kappa curve at a point (x ,y ) is:
2 x ( x 2 + y 2 ) + x 2 ( 2 x + 2 y d y d x ) = 2 a 2 y d y d x 2 x 3 + 2 x y 2 + 2 x 3 = 2 a 2 y d y d x − 2 x 2 y d y d x 4 x 3 + 2 x y 2 = ( 2 a 2 y − 2 x 2 y ) d y d x 2 x 3 + x y 2 a 2 y − x 2 y = d y d x {\displaystyle {\begin{aligned}2x\left(x^{2}+y^{2}\right)+x^{2}\left(2x+2y{\frac {dy}{dx}}\right)&=2a^{2}y{\frac {dy}{dx}}\\[6px]2x^{3}+2xy^{2}+2x^{3}&=2a^{2}y{\frac {dy}{dx}}-2x^{2}y{\frac {dy}{dx}}\\[6px]4x^{3}+2xy^{2}&=\left(2a^{2}y-2x^{2}y\right){\frac {dy}{dx}}\\[6px]{\frac {2x^{3}+xy^{2}}{a^{2}y-x^{2}y}}&={\frac {dy}{dx}}\end{aligned}}} 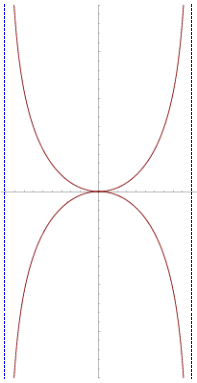


 French
French Deutsch
Deutsch






\left(x^{2}+y^{2}\right)+x^{2}(2x\,dx+2y\,dy)-a^{2}2y\,dy&=0\\[6px]\left(4x^{3}+2xy^{2}\right)dx+\left(2yx^{2}-2a^{2}y\right)dy&=0\\[6px]x\left(2x^{2}+y^{2}\right)dx+y\left(x^{2}-a^{2}\right)dy&=0\\[6px]{\frac {x\left(2x^{2}+y^{2}\right)}{y\left(a^{2}-x^{2}\right)}}&={\frac {dy}{dx}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2fbbee06e516acb095da379a192f66d2c38e956)
![{\displaystyle {\begin{aligned}2x\left(x^{2}+y^{2}\right)+x^{2}\left(2x+2y{\frac {dy}{dx}}\right)&=2a^{2}y{\frac {dy}{dx}}\\[6px]2x^{3}+2xy^{2}+2x^{3}&=2a^{2}y{\frac {dy}{dx}}-2x^{2}y{\frac {dy}{dx}}\\[6px]4x^{3}+2xy^{2}&=\left(2a^{2}y-2x^{2}y\right){\frac {dy}{dx}}\\[6px]{\frac {2x^{3}+xy^{2}}{a^{2}y-x^{2}y}}&={\frac {dy}{dx}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba914f68cdf1eee7a64e63203b830e54b63a6522)