Équation d'état de van der Waals — Wikipédia

En physique, et plus particulièrement en thermodynamique, l’équation d'état de van der Waals est une équation d'état des fluides réels proposée par le physicien Johannes Diderik van der Waals en 1873^[1],[2]. Elle lui valut le prix Nobel de physique en 1910 « pour ses travaux sur l'équation d'état des gaz et des liquides^[3]. »

La contribution fondamentale de van der Waals fut de modifier la loi des gaz parfaits en introduisant phénoménologiquement la taille finie des molécules ainsi que l'interaction attractive entre celles-ci. Le modèle des gaz parfaits, en effet, ne considère les particules que comme des sphères dures n'interagissant entre elles que par collision. Cette équation d'état peut également être établie à partir de la physique statistique^[4]. Concernant la taille des molécules, on peut déduire de l'équation de van der Waals le rayon de van der Waals. Les interactions à distance entre molécules sont appelées forces de van der Waals.

L'équation d'état de van der Waals fut historiquement une avancée considérable par rapport à l'équation des gaz parfaits, puisque, en plus de décrire le comportement d'un gaz réel plus précisément que le modèle des gaz parfaits (notamment les variations de température lors d'une détente de Joule-Thomson), cette équation décrit qualitativement la transition de phase liquide-gaz et présente un point critique. Elle guida Kamerlingh Onnes dans ses travaux sur la liquéfaction de l'hélium (1908)^[5] et fut à l'origine d'une véritable course au froid dans le but d'atteindre le zéro absolu^[6].

Grâce à sa simplicité d'utilisation, cette équation fut modifiée et améliorée à de nombreuses reprises, elle est la première d'une famille d'équations appelées équations d'état cubiques, parmi lesquelles on peut citer les plus connues : celle de Redlich-Kwong (1949), modifiée par Soave (1972), et celle de Peng-Robinson (1976).

Équation de van der Waals[modifier | modifier le code]

Formes diverses[modifier | modifier le code]

Forme extensive[modifier | modifier le code]

L'équation d'état de van der Waals s'écrit sous forme extensive :

Forme extensive : ${\displaystyle \left(P+{\frac {an^{2}}{V^{2}}}\right)\!\left(V-nb\right)=nRT}$

ou explicitement en pression :

${\displaystyle P={nRT \over V-nb}-{an^{2} \over V^{2}}}$

avec :

• ${\displaystyle a}$ le terme de cohésion (constant) ;
• ${\displaystyle b}$ le covolume molaire (constant) ;
• ${\displaystyle n}$ la quantité de matière (nombre de moles) ;
• ${\displaystyle P}$ la pression ;
• ${\displaystyle R}$ la constante universelle des gaz parfaits ;
• ${\displaystyle T}$ la température absolue ;
• ${\displaystyle V}$ le volume.

Les expressions des paramètres de l'équation de van der Waals en fonction des pression, température et volume molaire critiques sont données plus bas dans le paragraphe Les paramètres a et b. Si l'on considère le nombre de molécules à la place du nombre de moles :

${\displaystyle \left(P+{\frac {a^{\prime }N^{2}}{V^{2}}}\right)\!\left(V-Nb^{\prime }\right)=Nk_{\text{B}}T}$

avec :

• ${\displaystyle a^{\prime }={a \over {N_{\text{A}}}^{2}}}$ ;
• ${\displaystyle b^{\prime }={b \over N_{\text{A}}}}$ le volume d'exclusion d'une molécule ;
• ${\displaystyle k_{\text{B}}}$ la constante de Boltzmann ;
• ${\displaystyle N}$ le nombre de molécules, ${\displaystyle N=n\,N_{\text{A}}}$ ;
• ${\displaystyle N_{\text{A}}}$ le nombre d'Avogadro.

Rappelons que la constante universelle des gaz parfaits vaut ${\displaystyle R=N_{\text{A}}k_{\text{B}}}$.

Forme intensive[modifier | modifier le code]

L'équation d'état peut aussi s'écrire sous forme intensive :

Forme intensive : ${\displaystyle \left(P+{\frac {a}{{\bar {V}}^{2}}}\right)\!\left({\bar {V}}-b\right)=RT}$

avec ${\displaystyle {\bar {V}}}$ le volume molaire : ${\displaystyle {\bar {V}}={V \over n}}$.

Forme polynomiale[modifier | modifier le code]

En multipliant par ${\displaystyle {P^{2}{\bar {V}}^{2} \over R^{3}T^{3}}}$ la forme intensive, l'équation de van der Waals s'écrit également sous la forme d'un polynôme de degré trois en ${\displaystyle Z}$, le facteur de compressibilité. Historiquement, elle est la première des équations d'état cubiques :

Forme polynomiale : ${\displaystyle Z^{3}-\left(B+1\right)Z^{2}+AZ-AB=0}$

avec :

• ${\displaystyle A={aP \over R^{2}T^{2}}}$ le terme de cohésion normé ;
• ${\displaystyle B={bP \over RT}}$ le covolume molaire normé ;
• ${\displaystyle Z={P{\bar {V}} \over RT}}$ le facteur de compressibilité.

En comparaison, la loi des gaz parfaits revient à écrire ${\displaystyle Z=1}$.

Sous cette forme, l'équation d'état est facilement utilisable en employant la méthode de Cardan pour trouver les racines du polynôme. Lorsque l'équation d'état, à ${\displaystyle P}$, ${\displaystyle T}$ et composition données, donne une seule racine réelle, il peut s'agir soit d'un gaz, soit d'un liquide. Si l'équation d'état donne trois racines réelles, la plus grande, ${\displaystyle Z^{\text{max}}}$, permet de calculer le volume molaire d'un gaz, ${\displaystyle {\bar {V}}^{\text{g}}}$, selon : ${\displaystyle Z^{\text{max}}={P{\bar {V}}^{\text{g}} \over RT}}$ ; la plus petite, ${\displaystyle Z^{\text{min}}}$, permet de calculer le volume molaire d'un liquide, ${\displaystyle {\bar {V}}^{\text{l}}}$, selon : ${\displaystyle Z^{\text{min}}={P{\bar {V}}^{\text{l}} \over RT}}$ ; la racine intermédiaire n'a pas de réalité physique (voir le paragraphe Isothermes d'Andrews, diagramme de Clapeyron).

Forme réduite[modifier | modifier le code]

Selon la loi des états correspondants de van der Waals, le point critique joue un rôle important pour les gaz réels. L'équation de van der Waals peut enfin se réécrire sous forme réduite :

Forme réduite : ${\displaystyle \left(P_{\text{r}}+{3 \over {V_{\text{r}}}^{2}}\right)\!\left(V_{\text{r}}-{1 \over 3}\right)={8 \over 3}T_{\text{r}}}$

en introduisant les coordonnées réduites :

• ${\displaystyle P_{\text{r}}=P/P_{\text{c}}}$ la pression réduite ;
• ${\displaystyle T_{\text{r}}=T/T_{\text{c}}}$ la température réduite ;
• ${\displaystyle V_{\text{r}}={\bar {V}}/{\bar {V}}_{\text{c}}}$ le volume réduit ;

avec :

• ${\displaystyle P_{\text{c}}}$ la pression critique ;
• ${\displaystyle T_{\text{c}}}$ la température critique ;
• ${\displaystyle {\bar {V}}_{\text{c}}}$ le volume molaire critique.

Les expressions des pression, température et volume critiques en fonction des paramètres ${\displaystyle a}$ et ${\displaystyle b}$ de l'équation de van der Waals sont données plus bas dans le paragraphe Le point critique. Sous sa forme réduite, l'équation de van der Waals est indépendante de la nature du produit ; elle permet ainsi d'étudier l'équation d'état sans se rapporter à un produit spécifique, par exemple pour tracer les isothermes des figure 1 et figure 4.

Les paramètres a et b[modifier | modifier le code]

Paramètres pour un corps pur[modifier | modifier le code]

Pour un corps pur, les paramètres ${\displaystyle a}$ et ${\displaystyle b}$ sont calculés à partir des pression et température critiques (mesurables expérimentalement) selon :

Pour un corps pur : ${\displaystyle a={27R^{2}{T_{\text{c}}}^{2} \over 64P_{\text{c}}}\quad ;\quad b={R{T_{\text{c}}} \over 8P_{\text{c}}}}$

avec :

• ${\displaystyle P_{\text{c}}}$ la pression critique du corps pur ;
• ${\displaystyle T_{\text{c}}}$ la température critique du corps pur ;
• ${\displaystyle R}$ la constante universelle des gaz parfaits.

Paramètres pour un mélange[modifier | modifier le code]

Dans le cas d'un mélange de ${\displaystyle N}$ corps, les paramètres ${\displaystyle a}$ et ${\displaystyle b}$ sont calculés classiquement selon les règles de mélange suivantes, proposées par van der Waals en 1890^[7] :

Règles de mélange classiques : ${\displaystyle a_{m}=\sum _{i=1}^{N}\sum _{j=1}^{N}x_{i}x_{j}{\sqrt {a_{i}a_{j}}}\left(1-k_{i,j}\right)\quad ;\quad b_{m}=\sum _{i=1}^{N}x_{i}b_{i}}$

avec :

• ${\displaystyle x_{i}}$ la fraction molaire du corps ${\displaystyle i}$ ;
• ${\displaystyle a_{m}}$ le paramètre ${\displaystyle a}$ de l'équation de van der Waals pour le mélange ;
• ${\displaystyle a_{i}}$ le paramètre ${\displaystyle a}$ de l'équation de van der Waals pour le corps ${\displaystyle i}$ pur ;
• ${\displaystyle k_{i,j}}$ un paramètre d'interaction binaire entre le corps ${\displaystyle i}$ et le corps ${\displaystyle j}$, déterminé expérimentalement, avec ${\displaystyle k_{i,j}=k_{j,i}}$ et ${\displaystyle k_{i,i}=0}$ ;
• ${\displaystyle b_{m}}$ le paramètre ${\displaystyle b}$ de l'équation de van der Waals pour le mélange ;
• ${\displaystyle b_{i}}$ le paramètre ${\displaystyle b}$ de l'équation de van der Waals pour le corps ${\displaystyle i}$ pur.

Il existe d'autres règles de mélange, plus complexes et faisant intervenir d'autres paramètres. L'une des variantes les plus simples des règles de mélange classiques consiste à calculer le covolume selon :

${\displaystyle b_{m}={1 \over 2}\sum _{i=1}^{N}\sum _{j=1}^{N}x_{i}x_{j}\left(b_{i}+b_{j}\right)\left(1-l_{i,j}\right)}$

avec ${\displaystyle l_{i,j}}$ un paramètre d'interaction binaire entre le corps ${\displaystyle i}$ et le corps ${\displaystyle j}$, déterminé expérimentalement, avec ${\displaystyle l_{i,j}=l_{j,i}}$ et ${\displaystyle l_{i,i}=0}$. Si tous les ${\displaystyle l_{i,j}=0}$, cette règle revient à la règle classique.

Construction de l'équation[modifier | modifier le code]

Approche phénoménologique[modifier | modifier le code]

En pratique, les gaz ne se comportent pas exactement comme le décrit la loi des gaz parfaits, car ils sont composés de molécules ayant un certain volume. Le volume accessible à une particule est alors inférieur au volume de l'enceinte. La réduction du volume accessible est proportionnelle au nombre total de particules (ou nombre de moles). Le volume idéal de l'équation d'état des gaz parfaits, correspondant au volume total de l'enceinte puisque les particules y sont supposées de volume nul, est ainsi remplacé par :

${\displaystyle V_{\text{idéal}}=V_{\text{réel}}-nb}$

En outre, des interactions autres que les simples chocs élastiques du modèle des gaz parfaits existent entre les molécules. Les forces attractives entre les molécules font que la pression d'un gaz réel est inférieure à la pression d'un gaz idéal. L'équation de van der Waals s'obtient, contrairement à l'équation des gaz parfaits, à partir d'un modèle de gaz composé de sphères dures soumises à des interactions dipolaires attractives appelées forces de van der Waals, ce qui conduit à l'adaptation suivante :

${\displaystyle P_{\text{idéal}}=P_{\text{réel}}+{\frac {an^{2}}{V^{2}}}}$

En introduisant ces grandeurs dans l'équation des gaz parfaits :

${\displaystyle PV=nRT}$

on obtient l'équation de van der Waals :

${\displaystyle \left(P+{\frac {an^{2}}{V^{2}}}\right)\left(V-nb\right)=nRT}$

On remarque qu'à quantité de matière ${\displaystyle n}$ constante lorsque le volume ${\displaystyle V}$ devient très grand on a :

${\displaystyle P+{\frac {an^{2}}{V^{2}}}\approx P}$

${\displaystyle V-nb\approx V}$

on retrouve l'équation d'état du gaz parfait :

${\displaystyle PV=nRT}$

ce qui est cohérent avec le comportement des gaz réels.

Justification par la thermodynamique statistique[modifier | modifier le code]

La fonction de partition ${\displaystyle Z}$ (à ne pas confondre avec le facteur de compressibilité, également noté ${\displaystyle Z}$) d'un gaz parfait constitué de ${\displaystyle N=n\cdot N_{\text{A}}}$ particules identiques dans un volume ${\displaystyle V}$ est :

${\displaystyle Z={z^{N} \over N!}\quad {\hbox{avec}}\quad z={V \over \lambda ^{3}}}$

où ${\displaystyle \lambda }$ est la longueur d'onde thermique de de Broglie :

${\displaystyle \lambda ={\sqrt {h^{2} \over 2\pi mk_{\text{B}}T}}}$

avec :

• ${\displaystyle h}$ la constante de Planck ;
• ${\displaystyle m}$ la masse d'une particule ;
• ${\displaystyle k_{\text{B}}}$ la constante de Boltzmann ;
• ${\displaystyle T}$ la température ;
• ${\displaystyle z}$ la fonction de partition à une particule dans le volume ${\displaystyle V}$.

Pour les gaz réels, les particules sont considérées comme indépendantes, la relation ${\displaystyle Z=z^{N}/N!}$ est conservée pour l'ensemble de ${\displaystyle N}$ particules, mais la fonction de partition ${\displaystyle z}$ d'une particule est modifiée par les interactions de cette particule avec les autres particules. L'interaction entre deux particules est modélisée par un potentiel de Sutherland :

${\displaystyle u\!\left(r\right)={\begin{cases}\infty &{\hbox{quand}}\quad r<d\\-\epsilon \left({d \over r}\right)^{6}&{\hbox{quand}}\quad r\geq d\end{cases}}}$

avec :

• ${\displaystyle r}$ la distance entre les particules (entre les centres des sphères dures) ;
• ${\displaystyle d}$ la distance à laquelle les particules sont en contact (le double de leur rayon) ;
• ${\displaystyle \epsilon }$ l'intensité de la force de van der Waals entre les particules.

Premièrement, le volume occupé par l'ensemble des autres particules limite le volume accessible à une particule dans une enceinte de volume ${\displaystyle V}$. Les particules sont considérées comme des sphères dures toutes identiques de diamètre ${\displaystyle d}$ ; le volume d'une particule est donc égal à ${\displaystyle v_{\text{p}}=\pi d^{3}/6}$. Lorsque deux particules sont en contact, leurs centres sont à une distance l'un de l'autre égale à la somme du rayon de la particule 1 et du rayon de la particule 2, soit un diamètre ${\displaystyle d}$. Puisque les particules sont des sphères dures, les deux centres ne peuvent se situer à une distance inférieure à ${\displaystyle d}$ (interaction entre particules ${\displaystyle u\!\left(r\right)=\infty }$ quand ${\displaystyle r<d}$).

On choisit arbitrairement une particule cible et une seconde particule impactant la première. Lors d'une collision dans l'espace à trois dimensions, il existe ainsi autour de la particule cible une sphère d'exclusion de rayon ${\displaystyle d}$ et de volume : ${\displaystyle v_{\text{e}}={4 \over 3}\pi d^{3}=8v_{\text{p}}}$ dans laquelle le centre de la particule impactante ne peut pénétrer. Le choix de la particule cible et de la particule impactante étant arbitraire, il faut rapporter le volume d'exclusion aux deux particules ; le volume d'exclusion rapporté au nombre de particules en collision est de :

${\displaystyle b^{\prime }={1 \over 2}v_{\text{e}}={2 \over 3}\pi d^{3}}$

${\displaystyle b^{\prime }}$ n'est donc pas le volume d'une particule : ${\displaystyle b^{\prime }=4v_{\text{p}}}$. Pour un ensemble de ${\displaystyle N}$ particules, le volume d'exclusion total est de ${\displaystyle Nb^{\prime }}$. Le volume disponible pour une particule est ainsi corrigé en ${\displaystyle V-Nb^{\prime }}$.

Deuxièmement, la prise en compte des interactions entre particules est effectuée en calculant la fonction de partition ${\displaystyle z}$ d'une particule sensible au champ moyen créé par l'ensemble des autres particules. La concentration de ${\displaystyle N}$ particules dans un volume ${\displaystyle V}$ est égale à ${\displaystyle N/V}$, elle est considérée comme homogène dans tout le volume. On considère d'autre part une particule cible quelconque ; à une distance comprise entre ${\displaystyle r}$ et ${\displaystyle r+\mathrm {d} r}$ du centre de cette particule cible se trouvent ${\displaystyle {N \over V}4\pi r^{2}\,\mathrm {d} r}$ particules. L'énergie d'interaction entre ces particules et la particule cible est de ${\displaystyle u\!\left(r\right){N \over V}4\pi r^{2}\,\mathrm {d} r}$. Sur l'ensemble du volume ${\displaystyle V}$, l'énergie d'interaction ${\displaystyle \Phi }$ d'une particule avec le reste du gaz est égale à :

${\displaystyle \Phi =\int _{d}^{\infty }u\!\left(r\right){N \over V}4\pi r^{2}\,\mathrm {d} r=-2a^{\prime }{N \over V}}$

avec ${\displaystyle a^{\prime }=\epsilon {2\pi d^{3} \over 3}=\epsilon b^{\prime }}$. L'intégration est effectuée à partir de ${\displaystyle r=d}$ car, comme vu plus haut, il ne peut pas se trouver d'autre particule à une distance plus petite du centre de la particule cible.

La fonction de partition à une particule fait alors intervenir un facteur de Boltzmann ${\displaystyle \exp \!\left[-{\Phi \over 2k_{\text{B}}T}\right]}$. Le facteur 2 vient du partage de l'énergie d'interaction entre les deux particules concernées.

On obtient ainsi la fonction de partition corrigée pour une particule :

${\displaystyle z={\left(V-Nb^{\prime }\right)\,\exp \!\left[-{\Phi \over 2k_{\text{B}}T}\right] \over \lambda ^{3}}}$

puis la fonction de partition pour l'ensemble des ${\displaystyle N}$ particules :

${\displaystyle \ln Z=\ln \!\left({z^{N} \over N!}\right)=N\ln \!\left(V-Nb^{\prime }\right)+{N^{2}a^{\prime } \over Vk_{\text{B}}T}-N\ln \!\left(\lambda ^{3}\right)-\ln {N!}}$

La pression dans l'ensemble canonique se calcule à partir de :

${\displaystyle P=k_{\text{B}}T\,\left({\partial \ln Z \over \partial V}\right)_{T,N}}$

La dérivation des seuls termes impliquant le volume donne alors l'équation d'état de van der Waals :

${\displaystyle P={Nk_{\text{B}}T \over V-Nb^{\prime }}-{N^{2}a^{\prime } \over V^{2}}}$

${\displaystyle \left(P+{N^{2}a^{\prime } \over V^{2}}\right)\left(V-Nb^{\prime }\right)=Nk_{\text{B}}T}$

${\displaystyle \left(P+{n^{2}a \over V^{2}}\right)\left(V-nb\right)=nRT}$

avec :

• ${\displaystyle P}$ la pression du gaz ;
• ${\displaystyle T}$ la température absolue ;
• ${\displaystyle V}$ le volume ;
• ${\displaystyle b=b^{\prime }\cdot N_{\text{A}}}$ le covolume molaire ;
• ${\displaystyle b^{\prime }}$ le volume d'exclusion d'une particule ;
• ${\displaystyle a=a^{\prime }\cdot {N_{\text{A}}}^{2}}$ le terme de cohésion ;
• ${\displaystyle a^{\prime }=\epsilon b^{\prime }}$ ;
• ${\displaystyle R}$ la constante universelle des gaz parfaits, ${\displaystyle R=N_{\text{A}}\cdot k_{\text{B}}}$ ;
• ${\displaystyle N}$ le nombre de molécules ;
• ${\displaystyle n}$ la quantité de matière ou nombre de moles de gaz, ${\displaystyle n={N \over N_{\text{A}}}}$ ;
• ${\displaystyle N_{\text{A}}}$ le nombre d'Avogadro ;
• ${\displaystyle k_{\text{B}}}$ la constante de Boltzmann.

Étude de l'équation d'état de van der Waals[modifier | modifier le code]

Étude des isothermes[modifier | modifier le code]

Isothermes d'Andrews, diagramme de Clapeyron[modifier | modifier le code]

Pour tout corps pur réel, à température donnée, on peut tracer l'évolution de la pression en fonction du volume (à quantité de matière constante), ou du volume molaire (un diagramme portant le volume en abscisse et la pression en ordonnée est appelé diagramme de Clapeyron) : cette courbe est appelée courbe isotherme ${\displaystyle PV}$ ou isotherme d'Andrews. Pour un gaz parfait, la loi de Boyle-Mariotte indique que la courbe isotherme est une branche d'hyperbole, puisque ${\displaystyle P={nRT \over V}}$. La figure 1 montre sur le même graphique le tracé de plusieurs courbes isothermes obtenues pour un corps pur avec l'équation de van der Waals en coordonnées réduites :

${\displaystyle P_{\text{r}}={8T_{\text{r}} \over 3V_{\text{r}}-1}-{3 \over {V_{\text{r}}}^{2}}}$

Mathématiquement, les isothermes de l'équation d'état de van der Waals peuvent être tracées pour des volumes réduits allant de ${\displaystyle -\infty }$ à ${\displaystyle +\infty }$. Cependant, du point de vue de la théorie physique, les volumes réduits ne peuvent être inférieurs à ${\displaystyle {b/{\bar {V}}_{\text{c}}}={1/3}}$ selon cette équation. La droite verticale d'équation ${\displaystyle V_{\text{r}}=1/3}$ constitue une asymptote pour toutes les isothermes. De ce fait, les isothermes ne sont étudiées que dans le domaine des volumes réduits supérieurs à ${\displaystyle 1/3}$.

L'étude de ces courbes montre l'existence d'une température critique ${\displaystyle T_{\text{c}}}$ (courbe rouge de la figure 1) telle que :

• pour une température ${\displaystyle T>T_{\text{c}}}$ l'équation de van der Waals n'associe qu'un seul volume à une pression donnée (courbes vertes de la figure 1) : l'équation d'état cubique ne produit qu'une seule racine réelle (un seul volume molaire) quelle que soit la valeur de la pression ;
• pour une température ${\displaystyle T<T_{\text{c}}}$, le comportement est plus complexe (courbes bleu turquoise de la figure 1) : l'équation d'état cubique peut produire, selon la pression, une seule racine réelle (un seul volume molaire) ou trois racines réelles (trois volumes molaires).

Ces courbes sont interprétées comme suit :

• pour une température ${\displaystyle T>T_{\text{c}}}$ le fluide n'est stable que sous une seule phase : le fluide supercritique ;
• pour une température ${\displaystyle T<T_{\text{c}}}$ :
  • le fluide est stable sous une seule phase, gaz ou liquide, lorsque l'équation d'état ne produit qu'une seule racine réelle :
    • liquide pour de fortes pressions et de faibles volumes molaires ;
    • gaz pour de faibles pressions et de forts volumes molaires ;
  • le fluide peut être présent simultanément sous deux phases en équilibre, gaz et liquide, lorsque l'équation d'état produit trois racines réelles.

Le point critique[modifier | modifier le code]

La figure 2 montre l'allure des isothermes d'Andrews expérimentales. Dans ce diagramme, qui trace l'évolution de la pression en fonction du volume à température constante, une courbe isotherme à basse température est décroissante aux faibles volumes et fortes pressions, correspondant à un liquide, puis atteint un palier de pression constante, correspondant à un changement de phase liquide-vapeur, puis décroît pour de faibles pressions et de forts volumes, correspondant à un gaz. Les paliers de changement d'état sont donc horizontaux dans ce diagramme (paliers bleu turquoise de la figure 2). Plus la température augmente, plus la longueur du palier isobare correspondant diminue. Il existe une courbe, appelée isotherme critique, sur laquelle le palier est réduit à un point, appelé point critique (point C de la courbe rouge de la figure 1) : le liquide et le gaz ne s'y distinguent plus. Le point critique est donc un cas dégénéré de palier de changement d'état isobare. On en déduit que la tangente de la courbe isotherme critique en ce point doit être horizontale. De plus, puisque l'isotherme critique est décroissante monotone, elle traverse sa tangente en ce point : le point critique est un point d'inflexion. Au point critique la dérivée première (tangente horizontale) et la dérivée seconde (point d'inflexion) de la pression en fonction du volume, à température et quantité de matière constantes, sont par conséquent nulles^[8],[9],[10] :

Point critique : ${\displaystyle \left({\partial P \over \partial V}\right)_{T,n}=\left({\partial ^{2}P \over \partial V^{2}}\right)_{T,n}=0}$

Remarque 1 - Les isothermes peuvent présenter plusieurs points d'inflexion^[11]. Le point critique est le seul de toutes les isothermes où la tangente est horizontale dans le diagramme P-V.

Remarque 2 - La figure 2 est fausse, puisqu'au point critique la courbe critique y présente bien un point d'inflexion, mais que sa tangente n'y est pas horizontale ; la figure 1 est correcte de ce point de vue.

Avec l'équation d'état elle-même, on a un système de trois équations à trois inconnues (la pression, la température, le volume)^[9],[8],[12] :

${\displaystyle P={nRT \over V-nb}-{\frac {n^{2}a}{V^{2}}}}$

${\displaystyle \left({\partial P \over \partial V}\right)_{T,n}=-{nRT \over \left(V-nb\right)^{2}}+{2n^{2}a \over V^{3}}=0}$

${\displaystyle \left({\partial ^{2}P \over \partial V^{2}}\right)_{T,n}={2nRT \over \left(V-nb\right)^{3}}-{6n^{2}a \over V^{4}}=0}$

ou, en introduisant le volume molaire ${\displaystyle {\bar {V}}={V \over n}}$ :

${\displaystyle {RT \over {\bar {V}}-b}-{\frac {a}{{\bar {V}}^{2}}}=P}$

${\displaystyle -{RT \over \left({\bar {V}}-b\right)^{2}}+{2a \over {\bar {V}}^{3}}=0}$

${\displaystyle {2RT \over \left({\bar {V}}-b\right)^{3}}-{6a \over {\bar {V}}^{4}}=0}$

La solution, en introduisant les pression critique ${\displaystyle P_{\text{c}}}$, température critique ${\displaystyle T_{\text{c}}}$ et volume molaire critique ${\displaystyle {\bar {V}}_{\text{c}}}$, est^[9],[12] :

${\displaystyle P_{\text{c}}={a \over 27b^{2}}\quad ;\quad T_{\text{c}}={8a \over 27bR}\quad ;\quad {\bar {V}}_{\text{c}}=3b}$

Note : cette solution est unique. Comme indiqué dans la remarque précédente, le point critique est bien l'unique point d'inflexion parmi tous les points d'inflexion de toutes les isothermes, supercritiques et subcritiques, dont la tangente a une pente nulle dans le diagramme P-V.

Les pression et température critiques étant mesurables expérimentalement, on peut établir la valeur des paramètres ${\displaystyle a}$ et ${\displaystyle b}$^[8],[12] :

${\displaystyle a={27R^{2}{T_{\text{c}}}^{2} \over 64P_{\text{c}}}\quad ;\quad b={R{T_{\text{c}}} \over 8P_{\text{c}}}}$

Nous avons défini le facteur de compressibilité ${\displaystyle Z={P{\bar {V}} \over RT}}$. Au point critique, l'équation de van der Waals donne pour ce paramètre la valeur^[8],[12] :

${\displaystyle Z_{\text{c}}={\frac {P_{\text{c}}{\bar {V}}_{\text{c}}}{RT_{\text{c}}}}={\frac {3}{8}}=0{,}375}$

Selon l'équation de van der Waals le facteur de compressibilité critique ${\displaystyle Z_{\text{c}}}$ serait une constante universelle, mais cela ne correspond pas au comportement des gaz réels. En règle générale, le facteur de compressibilité critique vaut de 0,2 à 0,3^[13],[12]. On a par exemple respectivement pour l'hydrogène, l'éthane, l'ammoniac et l'eau :

${\displaystyle Z_{\text{c}}({\rm {H_{2}}})=0{,}304\quad ;\quad Z_{\text{c}}({\rm {C_{2}H_{6}}})=0{,}267\quad ;\quad Z_{\text{c}}({\rm {NH_{3}}})=0{,}238\quad ;\quad Z_{\text{c}}({\rm {H_{2}O}})=0{,}226}$

Les déviations observées montrent les limites de l'équation de van der Waals, qui ne peut représenter simultanément les trois propriétés critiques ${\displaystyle P_{\text{c}}}$, ${\displaystyle T_{\text{c}}}$ et ${\displaystyle V_{\text{c}}}$ avec seulement deux paramètres, ${\displaystyle a}$ et ${\displaystyle b}$. Toutefois, au regard de la loi des gaz parfaits selon laquelle ${\displaystyle Z=1}$ quelles que soient les conditions de pression et de température, y compris au point critique, l'équation de van der Waals fut une avancée considérable dans la représentation des fluides et la compréhension des phénomènes physiques associés.

Certaines équations d'état dérivées de l'équation de van der Waals utilisent un troisième paramètre, ${\displaystyle c}$, permettant de représenter simultanément les trois conditions du point critique. Cependant la mesure du volume molaire critique est difficile, étant donné les importantes fluctuations de la matière autour du point critique : le volume molaire critique est généralement mesuré avec une importante incertitude, ce paramètre n'est pas assez fiable pour être utilisé dans l'établissement d'une équation d'état.

Température de Boyle-Mariotte[modifier | modifier le code]

L'équation d'état de van der Waals donne :

${\displaystyle P={RT \over {\bar {V}}-b}-{a \over {\bar {V}}^{2}}}$

${\displaystyle Z={P{\bar {V}} \over RT}={1 \over 1-{b \over {\bar {V}}}}-{a \over RT{\bar {V}}}}$

Pour de grands volumes molaires, ${\displaystyle {\bar {V}}\gg b}$, soit ${\displaystyle {b \over {\bar {V}}}\approx 0}$, on a par développement limité :

${\displaystyle {1 \over 1-{b \over {\bar {V}}}}\approx 1+{b \over {\bar {V}}}+{b^{2} \over {\bar {V}}^{2}}+{b^{3} \over {\bar {V}}^{3}}+\cdots }$

Ce qui aboutit à un développement de l'équation d'état de van der Waals sous forme d'une équation du viriel^[14] :

${\displaystyle Z=1+\left(b-{a \over RT}\right)\!\cdot \!{1 \over {\bar {V}}}+{b^{2} \over {\bar {V}}^{2}}+{b^{3} \over {\bar {V}}^{3}}+\cdots }$

Le deuxième coefficient du viriel vaut :

${\displaystyle B_{2}=b-{a \over RT}}$

Il s'annule pour une température dite température de Boyle^[14], ou température de Boyle-Mariotte, notée ${\displaystyle T_{\text{B}}}$ :

${\displaystyle T_{\text{B}}={a \over bR}={27 \over 8}T_{\text{c}}=3{,}375\,T_{\text{c}}}$

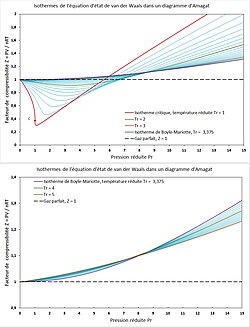
À cette température l'équation de van der Waals est au plus proche de l'équation d'état des gaz parfaits (${\displaystyle Z=1}$) : les forces d'attraction et de répulsion entre molécules de gaz s'y compensent exactement^[15]. La courbe isotherme correspondante est tracée sur la figure 3. Cette figure montre également qu'à basse pression le comportement d'un gaz de van der Waals se rapproche de celui d'un gaz parfait quelle que soit la température.

Isothermes dans un diagramme d'Amagat, courbe de Boyle-Mariotte[modifier | modifier le code]

Si l'on trace les isothermes d'un gaz parfait dans un diagramme d'Amagat, c'est-à-dire le produit de la pression et du volume ${\displaystyle PV}$ en fonction de la pression ${\displaystyle P}$ pour différentes températures ${\displaystyle T}$, on obtient des droites horizontales, puisque ${\displaystyle PV=nRT}$ est une constante à température ${\displaystyle T}$ donnée : il s'agit de la loi de Boyle-Mariotte. Pour un gaz réel ces isothermes sont décroissantes aux basses pressions puis croissantes aux hautes pressions. La figure 4 représente les isothermes réduites de van der Waals dans un diagramme d'Amagat : cette équation d'état représente qualitativement le phénomène physique réel. Cette figure représente également l'isotherme de Boyle-Mariotte définie à la température de Boyle-Mariotte ${\displaystyle T_{\text{B}}}$ établie précédemment.

Le lieu géométrique des minimums des isothermes est appelé courbe de Boyle-Mariotte^[16]. Cette courbe est donnée par la relation :

${\displaystyle \left({\partial PV \over \partial P}\right)_{T}=0}$

qui, puisque les coordonnées critiques sont des constantes, peut être écrite en coordonnées réduites :

${\displaystyle \left({\partial P_{\text{r}}V_{\text{r}} \over \partial P_{\text{r}}}\right)_{T_{\text{r}}}=0}$

que l'on peut développer et réarranger pour obtenir :

${\displaystyle -{V_{\text{r}} \over P_{\text{r}}}\left({\partial P_{\text{r}} \over \partial V_{\text{r}}}\right)_{T_{\text{r}}}=1}$

En utilisant la forme explicite réduite de l'équation de van der Waals :

${\displaystyle P_{\text{r}}={8T_{\text{r}} \over 3V_{\text{r}}-1}-{3 \over {V_{\text{r}}}^{2}}}$

on obtient :

${\displaystyle \left({\partial P_{\text{r}} \over \partial V_{\text{r}}}\right)_{T_{\text{r}}}=-3{8T_{\text{r}} \over \left(3V_{\text{r}}-1\right)^{2}}+{6 \over {V_{\text{r}}}^{2}}}$

en remplaçant ${\displaystyle {8T_{\text{r}} \over 3V_{\text{r}}-1}=P_{\text{r}}+{3 \over {V_{\text{r}}}^{2}}}$ et en réarrangeant :

${\displaystyle -{V_{\text{r}} \over P_{\text{r}}}\left({\partial P_{\text{r}} \over \partial V_{\text{r}}}\right)_{T_{\text{r}}}={3V_{\text{r}}\left({V_{\text{r}}}^{2}P_{\text{r}}+3\right)-6\left(3V_{\text{r}}-1\right) \over {V_{\text{r}}}^{2}P_{\text{r}}\left(3V_{\text{r}}-1\right)}}$

La relation ${\displaystyle -{V_{\text{r}} \over P_{\text{r}}}\left({\partial P_{\text{r}} \over \partial V_{\text{r}}}\right)_{T_{\text{r}}}=1}$ induit que :

${\displaystyle P_{\text{r}}={9 \over V_{\text{r}}}-{6 \over {V_{\text{r}}}^{2}}}$

On a donc :

${\displaystyle {1 \over V_{\text{r}}}={1 \over 6}\left(9-P_{\text{r}}V_{\text{r}}\right)}$

que l'on multiplie par ${\displaystyle P_{\text{r}}V_{\text{r}}}$ pour obtenir l'équation de la courbe de Boyle-Mariotte dans le diagramme d'Amagat :

Courbe de Boyle-Mariotte : ${\displaystyle P_{\text{r}}={1 \over 6}\left(9-P_{\text{r}}V_{\text{r}}\right)\cdot P_{\text{r}}V_{\text{r}}}$

Cette courbe est appelée ainsi car en chacun de ses points ${\displaystyle \left({\partial PV \over \partial P}\right)_{T}=0}$, comme pour un gaz parfait qui suit la loi de Boyle-Mariotte, à la différence près que pour le gaz parfait cette relation est vraie pour toute pression à toute température, donc en tout point du diagramme d'Amagat et non sur une unique courbe bien définie. Chacun des points de la courbe de Boyle-Mariotte est appelé point de Boyle-Mariotte de l'isotherme correspondante.

La courbe de Boyle-Mariotte intercepte l'isotherme de Boyle-Mariotte au point de coordonnées :

• ${\displaystyle P_{\text{r}}=0}$ ;
• ${\displaystyle V_{\text{r}}=+\infty }$, avec ${\displaystyle P_{\text{r}}V_{\text{r}}=9}$ ;
• ${\displaystyle T=T_{\text{B}}}$.

Au-delà de la température de Boyle-Mariotte les isothermes n'ont pas de point de Boyle-Mariotte et sont strictement croissantes dans le diagramme d'Amagat.

Le maximum de la courbe de Boyle-Mariotte a pour coordonnées :

• ${\displaystyle P_{\text{r}}^{\text{max}}={27 \over 8}}$, soit ${\displaystyle P^{\text{max}}={27 \over 8}P_{\text{c}}={a \over 8b^{2}}}$ ;
• ${\displaystyle V_{\text{r}}={4 \over 3}}$, soit ${\displaystyle {\bar {V}}={4 \over 3}{\bar {V}}_{\text{c}}=4b}$ ;
• ${\displaystyle T_{\text{r}}={243 \over 128}}$, soit ${\displaystyle T={243 \over 128}T_{\text{c}}={9a \over 16bR}}$.

Détente d'un gaz de van der Waals[modifier | modifier le code]

Détente de Joule-Gay-Lussac[modifier | modifier le code]

La détente de Joule-Gay-Lussac est une détente isoénergétique. Le coefficient de Joule-Gay-Lussac est défini par :

${\displaystyle \mu _{\text{JGL}}=\left({\partial T \over \partial V}\right)_{U}=-{\left(\beta T-1\right)P \over C_{V}}}$

avec :

• ${\displaystyle \beta }$ le coefficient de compression isochore ;
• ${\displaystyle C_{V}}$ la capacité thermique isochore.

Il permet de quantifier le changement de température subi par le gaz dans cette détente. Pour un gaz parfait, selon la loi de Joule et Gay-Lussac, ${\displaystyle \mu _{\text{JGL}}^{\bullet }=0}$ : un gaz parfait ne change pas de température dans une détente de Joule-Gay-Lussac.

Pour un gaz de van der Waals, on a :

${\displaystyle \beta \!\left(T,{\bar {V}}\right)={1 \over T}{1 \over \left(1-{a\left({\bar {V}}-b\right) \over RT{\bar {V}}^{2}}\right)}}$

Coefficient de Joule-Gay-Lussac : ${\displaystyle \mu _{\text{JGL}}=-{a \over {\bar {V}}^{2}C_{V}}}$

On a donc ${\displaystyle \mu _{\text{JGL}}<0}$ : dans une détente de Joule-Gay-Lussac, un gaz de van der Waals ne peut que refroidir (lorsque son volume augmente à énergie constante sa température diminue). C'est le cas de la majorité des gaz, à l'exception notable de l'hélium, de l'hydrogène et de certains gaz rares qui se réchauffent sous certaines conditions de température initiale dans une détente de ce type^[17].

Détente de Joule-Thomson[modifier | modifier le code]

La détente de Joule-Thomson est une détente isenthalpique. Le coefficient de Joule-Thomson est défini par^[18] :

${\displaystyle \mu _{\text{JT}}=\left({\partial T \over \partial P}\right)_{H}=-{\left(\alpha T-1\right)V \over C_{P}}}$

avec :

• ${\displaystyle \alpha }$ le coefficient de dilatation isobare ;
• ${\displaystyle C_{P}}$ la capacité thermique isobare.

Il permet de quantifier le changement de température subi par le gaz dans cette détente. Pour un gaz parfait, selon la loi de Joule-Thomson, ${\displaystyle \mu _{\text{JT}}^{\bullet }=0}$ : un gaz parfait ne change pas de température dans une détente de Joule-Thomson.

Pour un gaz de van der Waals, on a :

${\displaystyle \alpha \!\left(T,{\bar {V}}\right)={1 \over T}{1-{b \over {\bar {V}}} \over \left(1-{2a\left({\bar {V}}-b\right)^{2} \over RT{\bar {V}}^{3}}\right)}}$

Coefficient de Joule-Thomson : ${\displaystyle \mu _{\text{JT}}={{2a \over RT}\left({{\bar {V}}-b \over {\bar {V}}}\right)^{2}-b \over \left(1-{2a\left({\bar {V}}-b\right)^{2} \over RT{\bar {V}}^{3}}\right){\bar {C}}_{P}}}$

avec ${\displaystyle {\bar {C}}_{P}}$ la capacité thermique isobare molaire. Il existe donc des températures pour lesquelles ${\displaystyle \mu _{\text{JT}}=0}$ :

${\displaystyle {2a \over RT}\left({{\bar {V}}-b \over {\bar {V}}}\right)^{2}-b=0}$

${\displaystyle T={2a \over Rb}\left({{\bar {V}}-b \over {\bar {V}}}\right)^{2}}$

correspondant aux pressions :

${\displaystyle P={RT \over {\bar {V}}-b}-{a \over {\bar {V}}^{2}}={2a \over {\bar {V}}b}-{3a \over {\bar {V}}^{2}}}$

On peut écrire, en coordonnées réduites :

${\displaystyle T_{\text{r}}={T \over T_{\text{c}}}={27 \over 4}\left({V_{\text{r}}-{1 \over 3} \over V_{\text{r}}}\right)^{2}}$

${\displaystyle P_{\text{r}}={P \over P_{\text{c}}}={18 \over V_{\text{r}}}-{9 \over {V_{\text{r}}}^{2}}}$

et, puisque ${\displaystyle V_{\text{r}}>{1 \over 3}}$, on a la relation :

Courbe d'inversion de Joule-Thomson : ${\displaystyle P_{\text{r}}=9\left(3-2\cdot {\sqrt {T_{\text{r}} \over 3}}\right)\left(2\cdot {\sqrt {T_{\text{r}} \over 3}}-1\right)}$

Si l'on trace dans un diagramme ${\displaystyle TP}$ les courbes isenthalpes d'un gaz de van der Waals (voir figure 5), certaines courbes présentent un maximum. Le lieu géométrique des maximums est la courbe définie ci-dessus, elle délimite deux domaines^[18] :

• l'un dans lequel ${\displaystyle \mu _{\text{JT}}>0}$ aux basses pressions : lors d'une détente de Joule-Thomson le gaz se refroidit (lors d'une diminution de pression à enthalpie constante la température diminue) ;
• l'autre dans lequel ${\displaystyle \mu _{\text{JT}}<0}$ aux hautes pressions : lors d'une détente de Joule-Thomson le gaz se réchauffe (lors d'une diminution de pression à enthalpie constante la température augmente).

Un gaz ne peut donc être refroidi puis liquéfié^[18],[19] :

• par détente que si ${\displaystyle \mu _{\text{JT}}>0}$ ;
• par compression que si ${\displaystyle \mu _{\text{JT}}<0}$.

La pression ne pouvant être que positive, la courbe d'inversion admet deux limites à ${\displaystyle P=0}$^[18] :

• ${\displaystyle T_{\text{r}}^{\text{min}}={3 \over 4}}$, soit ${\displaystyle T^{\text{min}}={3 \over 4}T_{\text{c}}={2a \over 9bR}}$ ;
• ${\displaystyle T_{\text{r}}^{\text{max}}={27 \over 4}}$, soit ${\displaystyle T^{\text{max}}={27 \over 4}T_{\text{c}}={2a \over bR}}$.

Un gaz ne peut donc être refroidi par détente de Joule-Thomson que si ${\displaystyle T<T^{\text{max}}}$. Au-delà de ${\displaystyle T^{\text{max}}}$ un gaz se réchauffe dans une détente de Joule-Thomson quelle que soit la pression : les courbes isenthalpes sont strictement décroissantes, ${\displaystyle \mu _{\text{JT}}<0}$.

Le maximum de la courbe d'inversion a pour coordonnées :

• ${\displaystyle P_{\text{r}}^{\text{max}}=9}$, soit ${\displaystyle P^{\text{max}}=9P_{\text{c}}={a \over 3b^{2}}}$ ;
• ${\displaystyle T_{\text{r}}=3}$, soit ${\displaystyle T=3T_{\text{c}}={8a \over 9bR}}$.

Limites et défauts de l'équation[modifier | modifier le code]

L'équation de van der Waals fut historiquement une avancée considérable par rapport à l'équation des gaz parfaits, puisqu'elle représente qualitativement le comportement des fluides réels aussi bien par la présence d'un point critique que par la représentation des phases liquide et gaz en équilibre et hors équilibre. Elle présente cependant certains défauts.

Représentation de la zone critique et de la phase liquide[modifier | modifier le code]

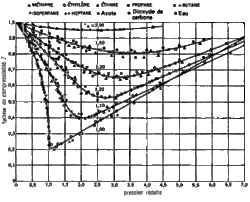
Comme toutes les équations d'état cubiques, l'équation d'état de van der Waals ne peut prétendre représenter correctement à la fois la zone du point critique (voir paragraphe Le point critique) et le comportement des phases liquides. La comparaison de la figure 3, qui représente les isothermes de l'équation d'état de van der Waals dans un diagramme d'Amagat, et de la figure 6, qui représente les isothermes dans le même diagramme pour quelques corps réels, montre un large décalage, par exemple, pour l'isotherme critique : la courbe critique calculée a un minimum à environ ${\displaystyle Z=0{,}3}$, les valeurs réelles peuvent descendre à environ ${\displaystyle Z=0{,}2}$.

Il a été démontré que ceci était inhérent à la forme même de ces équations, aussi sont-elles destinées à représenter les phases gaz avant toute chose. Les volumes molaires liquides produits par des équations d'état cubiques peuvent présenter d'importants écarts (en excès le plus souvent) par rapport à la réalité, en particulier à basse pression.

Représentation des équilibres liquide-vapeur[modifier | modifier le code]

Expérimentalement (voir figure 2), une courbe isotherme d'un corps pur aux fortes pressions et faibles volumes molaires décroît jusqu'à une pression appelée pression de vapeur saturante, notée ${\displaystyle P^{\text{sat}}}$ : cette branche représente la phase liquide. L'isotherme passe ensuite par un palier à pression constante représentant le changement de phase liquide-gaz. L'isotherme redécroît ensuite aux faibles pressions et forts volumes molaires, représentant la phase gaz.

L'équation de van der Waals ne montre pas ce palier et suggère pour un corps pur la coexistence des deux phases liquide et gaz sur une certaine plage de pression pour une même température : selon les isothermes bleu turquoise de la figure 1, la coexistence des deux phases serait possible entre les pressions des points I et K.

L'équation de van der Waals est donc incorrecte sur la zone de coexistence des deux phases liquide et gaz et ne permet pas le calcul direct des pressions de vapeur saturante. La règle du palier de Maxwell permet de corriger ce défaut (voir paragraphe Pression de vapeur saturante).

Zone de métastabilité, zone d'instabilité et pressions négatives[modifier | modifier le code]

Il est possible, à température donnée, dans certaines conditions très particulières, de maintenir de l'eau à l'état liquide sous une pression inférieure à sa pression de vapeur saturante (on parle de surchauffe ou retard à la vaporisation), de même qu'il est possible de maintenir de l'eau en phase gaz (vapeur d'eau) à une pression supérieure à sa pression de vapeur saturante (retard à la condensation). Ces états sont dits métastables et la moindre perturbation provoque l'évaporation violente de l'eau dans le premier cas et la liquéfaction brutale de la vapeur dans le second. Ces états sont similaires à celui de la surfusion dans lequel de l'eau est maintenue liquide en dessous de sa température de fusion et se solidifie à la moindre perturbation.

On peut également observer expérimentalement les pressions négatives obtenues pour la branche liquide des isothermes (isothermes bleu turquoise basses de la figure 1). Un tube de liquide placé dans une centrifugeuse subit une force qui peut être interprétée comme résultant d'une pression négative (ou tension)^[20]. De l'eau refroidie dans une volume constant peut rester liquide à une température de −15 °C, produisant une pression de −1 200 bar^[21]. On observe de l'eau liquide au sommet d'arbres de plus de 90 m de haut tel le Séquoia géant, alors que la capillarité ne peut faire monter l'eau à pression atmosphérique qu'à un maximum de 10 m : l'évaporation de l'eau dans les feuilles crée une pression de l'ordre de −4,8 atm dans des arbres de 60 m^[22],[23].

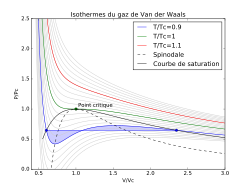
Ces états métastables sont dus aux forces d'attraction entre molécules que l'équation de van der Waals introduit via le paramètre ${\displaystyle a}$ : en l'absence d'impuretés, de sites de nucléation, une phase peut se maintenir au-delà des conditions habituelles de changement de phase. La surface comprise entre la courbe de saturation et la courbe spinodale représentées sur la figure 7 correspond au domaine de métastabilité des isothermes de van der Waals. L'équation de van der Waals représente donc plus ou moins ces états métastables respectivement par les branches LI et KG des isothermes bleu turquoise de la figure 1, ce qui est à porter à son crédit. Mais elle présente également sur ces mêmes isothermes une branche IJK qui s'appliquerait à une phase dont le volume molaire augmenterait avec une augmentation de pression : cet état serait thermodynamiquement instable, car de compressibilité ${\displaystyle \chi _{T}}$ négative, et n'a jamais été observé, il n'a pas de sens physique^[20]. La courbe spinodale représentée sur la figure 7 délimite le domaine d'instabilité des isothermes de van der Waals.

De façon générale, toute la partie des isothermes bleu turquoise comprise entre les points L et G (courbe LIJKG de la figure 1) n'est pas exploitable car peu, voire pas du tout, réaliste.

Absence de la phase solide[modifier | modifier le code]

Si l'équation d'état présente bien un point critique, le fluide supercritique et la transition liquide-gaz, elle ne présente pas de point triple et ne dit en conséquence rien des transitions liquide-solide et gaz-solide. L'équation d'état ne représente pas la phase solide. Aux basses températures (en dessous de la température triple) elle n'est donc utilisable que pour représenter un gaz.

Courbes isochores[modifier | modifier le code]

Si l'on trace la pression en fonction de la température à volume constant, les courbes isochores obtenues avec l'équation d'état de van der Waals sont des droites, ce qui n'est pas réaliste :

${\displaystyle P={nR \over V-nb}T-{an^{2} \over V^{2}}}$

Ceci implique aussi que la capacité thermique isochore ${\displaystyle C_{V}}$ d'un fluide de van der Waals ne dépend pas du volume, ce qui n'est également pas réaliste (voir paragraphe Capacité thermique isochore). D'autres équations d'état dérivées de l'équation d'état de van der Waals, comme l'équation d'état de Redlich-Kwong, celle de Soave-Redlich-Kwong et celle de Peng-Robinson, pour ne citer que les plus connues et les plus utilisées, tentent de corriger ce défaut en faisant dépendre le paramètre ${\displaystyle a}$ de la température.

Grandeurs calculables à partir de l'équation d'état de van der Waals[modifier | modifier le code]

Diverses grandeurs peuvent être calculées à partir de l'équation d'état de van der Waals, notamment la pression de vapeur saturante d'un corps pur, le coefficient de fugacité, les grandeurs résiduelles et les coefficients thermoélastiques.

Pression de vapeur saturante[modifier | modifier le code]

Ce qui suit n'est applicable qu'à un corps pur. Le calcul des pressions de bulle et de rosée d'un mélange est plus complexe et nécessite le calcul des coefficients de fugacité de chacun des composants du mélange.

Pour une température ${\displaystyle T}$ donnée inférieure à la température critique ${\displaystyle T_{\text{c}}}$ et des pressions ${\displaystyle P}$ inférieures à la pression critique ${\displaystyle P_{\text{c}}}$, l'équation de van der Waals peut produire trois valeurs du volume molaire ${\displaystyle {\bar {V}}}$ : le polynôme de degré trois en ${\displaystyle Z=P{\bar {V}}/RT}$ peut avoir trois racines réelles. La plus grande de ces racines permet alors le calcul d'un volume molaire attribuable à un gaz et noté ${\displaystyle {\bar {V}}^{\text{g}}}$. La plus petite de ces racines permet de calculer un volume molaire attribuable à un liquide et noté ${\displaystyle {\bar {V}}^{\text{l}}}$. La racine intermédiaire n'a pas de sens physique, il s'agirait d'une phase dont le volume molaire augmenterait avec une augmentation de pression, ce qui n'existe pas. Cependant, comme indiqué plus haut, l'équation de van der Waals suggère la coexistence stable des deux phases liquide et gaz sur une certaine plage de pression pour une même température pour un corps pur. Or l'expérience montre que pour un corps pur cette coexistence stable, ou équilibre, à température ${\displaystyle T}$ donnée, n'a lieu qu'à une seule pression : la pression de vapeur saturante notée ${\displaystyle P^{\text{sat}}\!\left(T\right)}$.

La règle du palier de Maxwell indique que le gaz et le liquide sont à l'équilibre si :

Règle du palier de Maxwell : ${\displaystyle \int _{{\bar {V}}^{\text{l}}}^{{\bar {V}}^{\text{g}}}P\,\mathrm {d} {\bar {V}}-P\!\cdot \!\left({\bar {V}}^{\text{g}}-{\bar {V}}^{\text{l}}\right)=0}$

Ce qui revient à dire que les deux surfaces violettes représentées sur la figure 7 sont égales. L'équation d'état de van der Waals donne :

${\displaystyle P=\frac{RT}{\stackrel{¯<!--\; ¯\; -->}{V}-<!--\; -\; -->b}-<!--\; -\; -->\frac{a}{{\stackrel{¯<!--\; ¯\; -->}{V}}^{}}}$