Последовательность «Посмотри-и-скажи» — Википедия

Последовательность «Посмотри-и-скажи» — это последовательность чисел, начинающаяся следующим образом:

1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211,… (последовательность A005150 в OEIS).

Каждое последующее число генерируется из предыдущего путём конкатенации цифры, из которой состоит группа одинаковых цифр и количества цифр в этой группе, для каждой группы одинаковых цифр в числе. Например:

1 читается как «одна единица», то есть 11
11 читается как «две единицы», то есть 21
21 читается как «одна двойка, одна единица», то есть 1211
1211 читается как «одна единица, одна двойка, две единицы», то есть 111221
111221 читается как «три единицы, две двойки, одна единица», то есть 312211
312211 читается как «одна тройка, одна единица, две двойки, две единицы», то есть 13112221

Последовательность «посмотри-и-скажи» была предложена Джоном Конвеем^[1].

Для произвольной цифры d, кроме единицы, в качестве начальной, последовательность принимает вид:

d, 1d, 111d, 311d, 13211d, 111312211d, 31131122211d, …

Основные свойства[править | править код]

Рост[править | править код]

Последовательность растёт бесконечно. Фактически, любой вариант последовательности с целым начальным числом будет расти бесконечно. Исключение составляет последовательность:

22, 22, 22, 22, 22, … (последовательность A010861 в OEIS).

Ограничение использующихся цифр[править | править код]

Никакие цифры, кроме 1, 2 и 3 не встречаются в последовательности, если начальное число не содержит других цифр или группы более чем из трёх цифр^[2].

Рост длины чисел[править | править код]

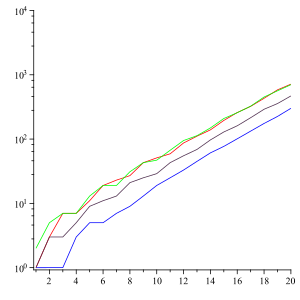
В среднем, числа вырастают на 30 % за итерацию. Если $L_{n}$ обозначает длину n-го члена последовательности, то существует предел отношения ${\frac {L_{n+1}}{L_{n}}}$ :

$\lim _{n\to \infty }{\frac {L_{n+1}}{L_{n}}}=\lambda$ .

Здесь λ = 1.303577269034… — постоянная Конвея^[2]. Тот же результат справедлив для любого варианта последовательности с начальным числом, отличным от 22.

Многочлен, возвращающий константу Конвея[править | править код]

Константа Конвея — это единственный положительный вещественный корень многочлена:

${\begin{aligned}&\,\,\,\,\,\,\,x^{71}&&&&-x^{69}&&-2x^{68}&&-x^{67}&&+2x^{66}&&+2x^{65}&&+x^{64}&&-x^{63}\\&-x^{62}&&-x^{61}&&-x^{60}&&-x^{59}&&+2x^{58}&&+5x^{57}&&+3x^{56}&&-2x^{55}&&-10x^{54}\\&-3x^{53}&&-2x^{52}&&+6x^{51}&&+6x^{50}&&+x^{49}&&+9x^{48}&&-3x^{47}&&-7x^{46}&&-8x^{45}\\&-8x^{44}&&+10x^{43}&&+6x^{42}&&+8x^{41}&&-5x^{40}&&-12x^{39}&&+7x^{38}&&-7x^{37}&&+7x^{36}\\&+x^{35}&&-3x^{34}&&+10x^{33}&&+x^{32}&&-6x^{31}&&-2x^{30}&&-10x^{29}&&-3x^{28}&&+2x^{27}\\&+9x^{26}&&-3x^{25}&&+14x^{24}&&-8x^{23}&&&&-7x^{21}&&+9x^{20}&&+3x^{19}&&-4x^{18}\\&-10x^{17}&&-7x^{16}&&+12x^{15}&&+7x^{14}&&+2x^{13}&&-12x^{12}&&-4x^{11}&&-2x^{10}&&+5x^{9}\\&&&+x^{7}&&-7x^{6}&&+7x^{5}&&-4x^{4}&&+12x^{3}&&-6x^{2}&&+3x&&-6\end{aligned}}$

В своей оригинальной статье Конвей совершает ошибку, написав «−» вместо «+» перед $x^{35}$ . Но значение λ, данное в его статье, верно^[3].

Популяризация[править | править код]

Последовательность «Посмотри-и-скажи» также известна как последовательность чисел Морриса в честь криптографа Роберта Морриса^[en]. Иногда упоминается как «яйцо кукушки» из-за головоломки «Какое следующее число в последовательности 1, 11, 21, 1211, 111221?», описанной Моррисом в книге Клиффорда Столла «Яйцо Кукушки».

Вариации[править | править код]

Существует много вариантов правил для создания последовательностей, подобных «Посмотри-и-скажи». Например, последовательность «pea pattern». Она отличается от «Посмотри-и-скажи» тем, что для получения нового числа в ней нужно подсчитывать все одинаковые цифры в числе. Начиная с числа 1, получим: 1, 11 (одна единица), 21 (две единицы), 1211 (одна двойка, одна единица), 3112 (три единицы, одна двойка), 132112 (одна тройка, две единицы, одна двойка), 312213 (три единицы, две двойки, одна тройка) и т. д. В итоге, последовательность приходит к циклу из двух чисел, 23322114 и 32232114.^[4]

Существует другой вариант, отличающийся от «pea pattern» тем, что цифры подсчитываются в порядке возрастания, а не по мере появления. Начиная с единицы, получим последовательность: 1, 11, 21, 1112, 3112, 211213, 312213, …

Эти последовательности имеют примечательные отличия от «Посмотри-и-скажи». В отличие от последовательности Конвея, данный член в «pea pattern» не однозначно определяет предыдущий член. Длина чисел в «pea pattern» ограничена и, для b-ричной системы счисления, не превышает 2b, и достигает 3b для больших начальных чисел (например, «сто единиц»).

Учитывая, что эта последовательность бесконечна и длина её ограничена, она должна в конечном итоге повториться, по принципу Дирихле. Как следствие, эти последовательности всегда периодические.

См. также[править | править код]

Примечания[править | править код]

↑ John Horton Conway. The Weird and Wonderful Chemistry of Audioactive Decay (англ.) // Eureka. — 1986. — January (vol. 46). — P. 5—16. Архивировано 11 октября 2014 года.
↑ ¹ ² Oscar Martin. Look-and-Say Biochemistry: Exponential RNA and Multistranded DNA (англ.) // American Mathematical Monthly. — 2006. — Vol. 113, no. 4. — P. 289—307. — ISSN 0002-9890. Архивировано 24 декабря 2006 года.
↑ Ilan Vardi. Computational Recreation in Mathematica.
↑ Ascending Pea Pattern generator (неопр.). Дата обращения: 9 августа 2018. Архивировано 17 октября 2016 года.

[1] John Horton Conway. The Weird and Wonderful Chemistry of Audioactive Decay (англ.) // Eureka. — 1986. — January (vol. 46). — P. 5—16. Архивировано 11 октября 2014 года.

[:2-2] ¹ ² Oscar Martin. Look-and-Say Biochemistry: Exponential RNA and Multistranded DNA (англ.) // American Mathematical Monthly. — 2006. — Vol. 113, no. 4. — P. 289—307. — ISSN 0002-9890. Архивировано 24 декабря 2006 года.

[3] Ilan Vardi. Computational Recreation in Mathematica.

[4] Ascending Pea Pattern generator (неопр.). Дата обращения: 9 августа 2018. Архивировано 17 октября 2016 года.

[1]

[2]

[3]

[4]