Список правильных многомерных многогранников и соединений — Википедия

Примеры правильных многогранников

Правильные (2D) многоугольники
Выпуклые	Звёздчатые
{5}	{5/2}
Правильные 3D-многогранники
Выпуклые	Звёздчатые
{5,3}	{5/2,5}
Правильные 2D-замощения
Евклидовы	Гиперболические
{4,4}	{5,4}[англ.]
Правильные 4D-многогранники
Выпуклые	Звёздчатые
{5,3,3}	{5/2,5,3}[англ.]
Правильные 3D-замощения
Евклидовы	Гиперболические
{4,3,4}	{5,3,4}

Эта страница содержит список правильных многомерных многогранников (политопов) и правильных cоединений этих многогранников в евклидовом, сферическом и гиперболическом пространствах разных размерностей.

Символ Шлефли описывает каждое правильное замощение n-сферы, евклидова и гиперболического пространства. Символ Шлефли описания n-мерного многогранника равным образом описывает мозаику (n-1)-сферы. Вдобавок, симметрия правильного многогранника или замощения выражается как группа Коксетера, которые Коксетер обозначал идентично символам Шлефли, за исключением разграничения квадратными скобками, и эта нотация называется нотацией Коксетера^[англ.]. Другой связанный символ — диаграмма Коксетера — Дынкина, которая представляет группу симметрии (без помеченных кружком узлов) и правильные многогранники или замощения с обведённым кружком первым узлом. Например, куб имеет символ Шлефли {4,3}, с его октаэдральной симметрией^[англ.] [4,3] или , представляется диаграммой Коксетера .

Правильные многогранники сгруппированы по размерности, а затем по форме — выпуклые, невыпуклые и бесконечные. Невыпуклые виды используют те же вершины, что и выпуклые, но имеют пересекающиеся фасеты (грани максимальной размерности = размерности пространства – 1). Бесконечные виды замощают евклидово пространство на единицу меньшей размерности.

Бесконечные формы можно расширить до замощения гиперболического пространства. Гиперболическое пространство подобно обычному пространству, но параллельные прямые с расстоянием расходятся. Это позволяет вершинным фигурам иметь отрицательные угловые дефекты. Например, в вершине может сходиться семь правильных треугольников, лежащих на плоскости. Это нельзя осуществить на обычной (евклидовой) плоскости, но можно сделать при некотором масштабе на гиперболической плоскости.

Многогранники, удовлетворяющие более общему определению и не имеющие простых символов Шлефли, включают правильные косые многогранники и бесконечноугольные правильные косые многогранники с неплоскими фасетами или вершинными фигурами.

Таблица показывает сводку правильных многогранников по размерностям.

	Конечные			Евклидовы	Гиперболические			Соединения
Разм.	Выпук- лые	Звёзд- чатые	Косые	Выпук- лые	Компак- тные	Звёзд- чатые	Параком- пактные	Выпук- лые	Звёзд- чатые
1	1	0	0	1	0	0	0	0	0
2	∞	∞	∞	1	1	0	0	∞	∞
3	5	4	?	3	∞	∞	∞	5	0
4	6	10	?	1	4	0	11	26	20
5	3	0	?	3	5	4	2	0	0
6	3	0	?	1	0	0	5	0	0
7	3	0	?	1	0	0	0	3	0
8	3	0	?	1	0	0	0	6	0
9+	3	0	?	1	0	0	0	*	0

* 1, если размерность имеет вид 2^k − 1; 2, если размерность является степенью двойки; 0 в противном случае.

Не существует правильных звёздчатых замощений в евклидовом пространстве любой размерности.

Диаграмма Коксетера — Дынкина представляет зеркальные "плоскости" как узлы, и помещает кружок вокруг узла, если точка не лежит на плоскости. Отрезок, { }, — это точка p и зеркальный образ точки p, а также отрезок между ними.

Одномерный многогранник (1-многогранник) — это замкнутый отрезок, ограниченный двумя конечными точками. 1-многогранник является правильным по определению и представляется символом Шлефли { }^[1][2] или диаграммой Коксетера с единственным помеченным кружком узлом, . Норман Джонсон дал им название дайтел и символ Шлефли { } ^[3].

Будучи тривиальным в качестве многогранника, дайтел возникает в качестве рёбер многоугольников и многогранников^[4]. Он используется в определении однородных призм (как в символе Шлефли { }×{p}) или в диаграмме Коксетера как прямое произведение отрезка и правильного многоугольника ^[5].

Двумерные многогранники называются многоугольниками. Правильные многоугольники имеют равные стороны и вписаны в окружность. Правильный p-угольник представляется символом Шлефли {p}.

Обычно только выпуклые многоугольники считаются правильными, но звёздчатые многоугольники наподобие пентаграммы можно также считать правильными. Они используют те же вершины, что и выпуклые формы, но соединение происходит другим путём, при котором окружность обходится более одного раза.

Звёздчатые многоугольники следует называть скорее невыпуклыми, чем вогнутыми, поскольку пересечение рёбер не образует новых вершин и все вершины находятся на окружности.

Символ Шлефли {p} представляет правильный p-угольник.

Название	Треугольник (2-симплекс)	Квадрат (2-ортоплекс) (2-куб)	Пятиугольник	Шестиугольник	Семиугольник	Восьмиугольник
Шлефли	{3}	{4}	{5}	{6}	{7}	{8}
Симметрия	D3, [3]	D4, [4]	D5, [5]	D6, [6]	D7, [7]	D8, [8]
Коксетер
Рисунок
Название	Девятиугольник	Десятиугольник	Одиннадцатиугольник	Двенадцатиугольник	Тринадцатиугольник	Четырнадцатиугольник
Шлефли	{9}	{10}	{11}	{12}	{13}	{14}
Симметрия	D9, [9]	D10, [10]	D11, [11]	D12, [12]	D13, [13]	D14, [14]
Дынкин
Рисунок
Название	Пятнадцатиугольник	Шестнадцатиугольник	Семнадцатиугольник	Восемнадцатиугольник	Девятнадцатиугольник	Двадцатиугольник	...p-угольник
Шлефли	{15}	{16}	{17}	{18}	{19}	{20}	{p}
Симметрия	D15, [15]	D16, [16]	D17, [17]	D18, [18]	D19, [19]	D20, [20]	Dp, [p]
Дынкин
Рисунок

Правильный двуугольник {2} можно считать вырожденным правильным многоугольником. Он может существовать как невырожденный в некоторых неевклидовых пространствах, таких как поверхность сферы или тора.

Название	Одноугольник	Двуугольник
Символ Шлефли	{1}	{2}
Симметрия	D1, [ ]	D2, [2]
Коксетер diagram	или
Рисунок

Существует бесконечно много правильных звёздчатых многогранников в двумерном пространстве (т.е. многоугольников), символы Шлефли которых являются рациональными числами {n/m}. Они называются звёздчатыми многоугольниками и имеют то же самое расположение вершин^[англ.], что и у выпуклого многоугольника.

В общем случае для любого натурального числа n и для всех m, таких, что m < n/2 и m, n взаимно просты, существуют n-точечные правильные звёзды с символами Шлефли {n/m} (строго говоря, {n/m}={n/(n−m)}) .

Название	Пентаграмма	Гептаграммы		Октаграмма	Эннеаграммы		Декаграмма[англ.]	...n-граммы
Шлефли	{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	{9/4}	{10/3}	{p/q}
Симметрия	D5, [5]	D7, [7]		D8, [8]	D9, [9],		D10, [10]	Dp, [p]
Коксетер
Рисунок

Правильные звёздчатые многоугольники с числом сторон до 20

{11/2}	{11/3}	{11/4}	{11/5}	{12/5}	{13/2}	{13/3}	{13/4}	{13/5}	{13/6}
{14/3}	{14/5}	{15/2}	{15/4}	{15/7}	{16/3}	{16/5}	{16/7}
{17/2}	{17/3}	{17/4}	{17/5}	{17/6}	{17/7}	{17/8}	{18/5}	{18/7}
{19/2}	{19/3}	{19/4}	{19/5}	{19/6}	{19/7}	{19/8}	{19/9}	{20/3}	{20/7}	{20/9}

В 3-мерном пространстве правильный пространственный многоугольник ^[6] называется антипризматическим многоугольником и он имеет то же расположение вершин^[англ.], что и у антипризмы, и его рёбра являются подмножеством рёбер антипризмы, соединяющие зигзагом вершины верхнего и нижнего многоугольников.

Пример правильного пространственного зигзаг-многоугольника

Шестиугольник	Восьмиугольник	Десятиугольник
D3d, [2+,6]	D4d, [2+,8]	D5d, [2+,10]
{3}#{ }	{4}#{ }	{5}#{ }	{5/2}#{ }	{5/3}#{ }

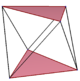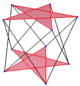В 4-мерном пространстве правильный пространственный многоугольник может иметь вершины на торе Клиффорда и связан с вращением Клиффорда^[англ.]. В отличие от антипризматичных пространственных многоугольников, пространственные многоугольники двойного вращения могут иметь нечётное число сторон.

Их можно видеть в многоугольниках Петри выпуклых правильных четырёхмерных многогранников^[англ.], видимые как правильные плоские многоугольники периметров проекций Коксетера:

Пятиугольник	Восьмиугольник	Двенадцатиугольник	Тридцатиугольник
Пятиячейник	Шестнадцатиячейник	Двадцатичетырёхъячейник	Шестисотячейник

В трёхмерном пространстве правильный многогранник с символом Шлефли {p,q} и диаграммой Коксетера имеет правильные грани вида {p} и правильную вершинную фигуру {q}.

Вершинная фигура (многогранника) является многоугольником, получаемым соединением вершин, отстоящих на одно ребро от заданной вершины. Для правильных трёхмерных многогранников, эта вершинная фигура является всегда правильным (и планарным) многоугольником.

Существование правильного многогранника {p,q} ограничено неравенством, относящимся к угловому дефекту вершинной фигуры:

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}>{\frac {1}{2}}}$ : Многогранник (существует в евклидовом 3-мерном пространстве)

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{2}}}$ : Евклидова плоская мозаика

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}<{\frac {1}{2}}}$ : Замощение гиперболической плоскости

Перенумеровав перестановки, мы найдём 5 выпуклых форм, 4 звёздчатые формы и 3 плоских замощения, все с многоугольниками {p} и {q} из списка: {3}, {4}, {5}, {5/2} и {6}.

Вдобавок к мозаикам евклидова пространства существует бесконечное количество правильных гиперболических мозаик.

Пять выпуклых правильных многогранников называются платоновыми телами. Вершинная фигура указана вместе с числом вершин. Все эти многогранники имеют эйлерову характеристику (χ) 2.

Название	Шлефли {p,q}	Коксетер	Рисунок (прозрачный)	Рисунок (тело)	Рисунок (сфера)	Граней {p}	Рёбер	Вершин {q}	Симметрия	Двойственный
Тетраэдр (3-симплекс)	{3,3}					4 {3}	6	4 {3}	Td [3,3] (*332)	(самодвойственен)
Шестигранник Куб (3-куб)	{4,3}					6 {4}	12	8 {3}	Oh [4,3] (*432)	Октаэдр
Октаэдр (3-ортоплекс)	{3,4}					8 {3}	12	6 {4}	Oh [4,3] (*432)	Куб
Додекаэдр	{5,3}					12 {5}	30	20 {3}	Ih [5,3] (*532)	Икосаэдр
Икосаэдр	{3,5}					20 {3}	30	12 {5}	Ih [5,3] (*532)	Додекаэдр

В сферической геометрии существуют правильные сферические многогранники (мозаики на cфере), которые в нормальном случае являются вырожденными многогранниками. Это осоэдры {2,n} и двойственные им диэдры {n,2}. Коксетер называет такие случаи "несобственными" замощениями ^[7].

Несколько первых примеров (n от 2 до 6) приведены ниже.

Осоэдры

Название	Шлефли {2,p}	Коксетер diagram	Рисунок (sphere)	Граней {2}π/p	Рёбер	Вершин {p}	Симметрия	Двойственный
Двуугольный осоэдр	{2,2}		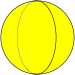	2 {2}π/2	2	2 {2}π/2	D2h [2,2] (*222)	Самодвойственен
Треугольный осоэдр	{2,3}			3 {2}π/3	3	2 {3}	D3h [2,3] (*322)	Треугольный диэдр
Квадратный осоэдр	{2,4}		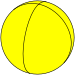	4 {2}π/4	4	2 {4}	D4h [2,4] (*422)	Квадратный диэдр
Пятиугольный осоэдр	{2,5}		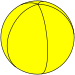	5 {2}π/5	5	2 {5}	D5h [2,5] (*522)	Пятиугольный диэдр
Шестиугольный осоэдр	{2,6}			6 {2}π/6	6	2 {6}	D6h [2,6] (*622)	Шестиугольный диэдр

Диэдры

Название	Шлефли {p,2}	Диаграмма Коксетера	Рисунок (сфера)	Граней {p}	Рёбер	Вершин {2}	Симметрия	Двойственный
Двуугольный диэдр	{2,2}			2 {2}π/2	2	2 {2}π/2	D2h [2,2] (*222)	Самодвойственен
Треугольный диэдр	{3,2}			2 {3}	3	3 {2}π/3	D3h [3,2] (*322)	Треугольный осоэдр
Квадратный диэдр	{4,2}			2 {4}	4	4 {2}π/4	D4h [4,2] (*422)	Квадратный осоэдр
Пятиугольный диэдр	{5,2}			2 {5}	5	5 {2}π/5	D5h [5,2] (*522)	Пятиугольный осоэдр
Шестиугольный диэдр	{6,2}			2 {6}	6	6 {2}π/6	D6h [6,2] (*622)	Шестиугольный осоэдр

Звёздчатые диэдры и осоэдры также существуют, такие как {5/2,2} и {2,5/2}.

Правильные звёздчатые многогранники называются телами Кеплера — Пуансо и их существует четыре. Они основываются на расположении вершин^[англ.] додекаэдра {5,3} и икосаэдра {3,5}:

Как cферические мозаики эти звёздчатые формы перекрывают сферу несколько раз, что называется их плотностью. Для этих форм плотность равна 3 или 7. Рисунки мозаик показывают грани отдельных сферических многоугольников жёлтым цветом.

Название	Рисунок (прозрачный)	Рисунок (непрозрачный)	Рисунок (сферический)	Диаграмма образования звёздчатой формы	Шлефли {p,q} и Коксетер	Граней {p}	Рёбер	Вершин {q} Фигура	χ	Плот- ность[англ.]	Симметрия	Двойственный
Малый звёздчатый додекаэдр					{5/2,5}	12 {5/2}	30	12 {5}	−6	3	Ih [5,3] (*532)	Большой додекаэдр
Большой додекаэдр					{5,5/2}	12 {5}	30	12 {5/2}	−6	3	Ih [5,3] (*532)	Малый звёздчатый додекаэдр
Большой звёздчатый додекаэдр					{5/2,3}	12 {5/2}	30	20 {3}	2	7	Ih [5,3] (*532)	Большой икосаэдр
Большой икосаэдр					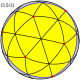{3,5/2}	20 {3}	30	12 {5/2}	2	7	Ih [5,3] (*532)	Большой звёздчатый додекаэдр

Правильный косой многогранник является обобщением множества правильных многогранников, в котором допускается непланарность вершинных фигур.

Для 4-мерных косых многогранников Коксетер предложил модифицированный символ Шлефли {l,m|n}, имеющих вершинную фигуру {l,m}, m l-угольников вокруг вершины с n-угольными дырами. Их вершинные фигуры являются пространственными многоугольниками, представляющими зигзаги между двумя плоскостями.

Для правильных косых многогранников, представленных символом {l,m|n}, выполняется равенство:

2*sin(π/l)*sin(π/m)=cos(π/n)

Четыре из них можно видеть в 4-мерном пространстве как множество граней четырёх правильных четырёхмерных многогранников, имеющих одно и то же расположение вершин^[англ.] и расположение рёбер^[англ.]:

{4, 6 | 3}	{6, 4 | 3}	{4, 8 | 3}	{8, 4 | 3}

Правильные 4-мерные многогранники с символом Шлефли ${\displaystyle \{p,q,r\}}$ имеют ячейки вида ${\displaystyle \{p,q\}}$, грани вида ${\displaystyle \{p\}}$, рёберные фигуры ${\displaystyle \{r\}}$ и вершинные фигуры ${\displaystyle \{q,r\}}$.

• Вершинная фигура (4-мерного многогранника) является (3-мерным) многогранником, образованным соседними к данной вершине вершинами многогранника. Для правильных четырёхмерных многогранников эта вершинная фигура является правильным (3-мерным) многогранником.
• Рёберной фигурой является многоугольник, образованный прилегающими к ребру гранями. Для правильных четырёхмерных многогранников рёберной фигурой всегда будет правильный многоугольник.

Существование правильных четырёхмерных многогранников ${\displaystyle \{p,q,r\}}$ ограничено существованием правильного многогранника ${\displaystyle \{p,q\},\{q,r\}}$. Для 4-мерных многогранников предлагается использовать название "полихор"^[8][9]

Каждый вид может существовать в пространстве, зависящем от следующего выражения:

${\displaystyle \sin \left({\frac {\pi }{p}}\right)\sin \left({\frac {\pi }{r}}\right)-\cos \left({\frac {\pi }{q}}\right)}$

${\displaystyle >0}$ : Гиперсферические 3-мерные соты или 4-мерные многогранники

${\displaystyle =0}$ : евклидовы 3-мерные соты

${\displaystyle <0}$ : Гиперболические 3-мерные соты

Эти ограничения допустимы для 21 форм — 6 форм выпуклы, 10 не выпуклы, одна является евклидовыми 3-мерными сотами и 4 являются гиперболическими сотами.

Эйлерова характеристика ${\displaystyle \chi }$ четырёхмерного многогранника вычисляется по формуле ${\displaystyle \chi =V+F-E-C}$ и равна нулю для всех видов.

6 выпуклых правильных четырёхмерных многогранников показаны в таблице ниже. Все эти многогранники имеют эйлерову характеристику (χ) 0.

Название	Шлефли {p,q,r}	Коксетер	Ячейки[англ.] {p,q}	Граней {p}	Рёбер {r}	Вершин {q,r}	Двойственный {r,q,p}
Пятиячейник (4-симплекс)	{3,3,3}		5 {3,3}	10 {3}	10 {3}	5 {3,3}	(самодвойственен)
Тессеракт (4-куб)	{4,3,3}		8 {4,3}	24 {4}	32 {3}	16 {3,3}	Шестнадцатиячейник
Шестнадцатиячейник (4-ортоплекс)	{3,3,4}		16 {3,3}	32 {3}	24 {4}	8 {3,4}	Тессеракт
Двадцатичетырёхъячейник	{3,4,3}		24 {3,4}	96 {3}	96 {3}	24 {4,3}	(самодвойственен)
Стодвадцатиячейник	{5,3,3}		120 {5,3}	720 {5}	1200 {3}	600 {3,3}	Шестисотъячейник
Шестисотъячейник	{3,3,5}		600 {3,3}	1200 {3}	720 {5}	120 {3,5}	Стодвадцатиячейник

Пятиячейник	Тессеракт	Шестнадцати- ячейник	Двадцати- четырёхъячейник	Стодвадцати- ячейник	Шестисотъячейник
{3,3,3}	{4,3,3}	{3,3,4}	{3,4,3}	{5,3,3}	{3,3,5}
Каркас (Многоугольник Петри) в косой ортогональной проекции
Ортогональная проекция
Тетраэдральная оболочка (центрировано по ячейке/вершине)	Кубическая оболочка (центрировано по ячейке)	Кубическая оболочка (центрировано по ячейке)	Кубооктаэдральная оболочка (центрировано по ячейке)	Усечённая ромботриаконта- эдральная оболочка[англ.] (центрировано по ячейке)	Пентакиикоси- додекаэдральная оболочка[англ.] (центрировано по вершине)
Диаграммы Шлегеля (перспективная проекция)
(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по вершине)
Каркас стереографической проекции (гиперсферический)

4-мерные диэдры и осоэдры существуют как правильные замощения 3-сферы.

Правильные 4-мерные диэдры (2 фасеты = 3-мерные грани) включают: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2}, {p,2,2} и их двойственные 4-мерные осоэдры (2 вершины): {2,3,3}, {2,4,3}, {2,3,4}, {2,3,5}, {2,5,3}, {2,2,p}. Многогранники вида {2,p,2} являются одновременно 4-мерными диэдрами и осоэдрами. Существуют также формы {p,2,q}, которые имеют диэдральные ячейки и осоэдральные вершинные фигуры.

Правильные 4-мерные осоэдры как соты на 3-сфере

Шлефли {2,p,q}	Коксетер	Ячейки[англ.] {2,p}π/q	Граней {2}π/p,π/q	Рёбер	Вершин	Вершинная фигура {p,q}	Симметрия	Двойственный
{2,3,3}		4 {2,3}π/3	6 {2}π/3,π/3	4	2	{3,3}	[2,3,3]	{3,3,2}
{2,4,3}		6 {2,4}π/3	12 {2}π/4,π/3	8	2	{4,3}	[2,4,3]	{3,4,2}
{2,3,4}		8 {2,3}π/4	12 {2}π/3,π/4	6	2	{3,4}	[2,4,3]	{4,3,2}
{2,5,3}		12 {2,5}π/3	30 {2}π/5,π/3	20	2	{5,3}	[2,5,3]	{3,5,2}
{2,3,5}		20 {2,3}π/5	30 {2}π/3,π/5	12	2	{3,5}	[2,5,3]	{5,3,2}

Существует десять правильных 4-мерных звёздчатых многогранника, которые называются многогранниками Шлефли—Гесса^[англ.]. Их вершины располагаются на выпуклом стодвадцатиячейнике {5,3,3} и шестисотъячейнике {3,3,5}.

Людвиг Шлефли нашёл четыре из них и отбросил остальные шесть, поскольку не позволял нарушение эйлеровой характеристики на ячейках или вершинных фигурах (F+V−E=2). Эдмунд Гесс (Edmund Hess, 1843–1903) завершил список в своей книге Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder ([3], 1883) (Введение в учение о замощении сферы с учётом теории равногранных и равноугольных многогранников) .

Существует 4 расположения рёбер^[англ.] и 7 расположений граней^[англ.] в этих 10 правильных звёздчатых 4-мерных многогранниках, показанные как ортогональные проекции:

Название	Каркас	Тело	Шлефли {p, q, r} Коксетер	Ячеек {p, q}	Граней {p}	Рёбер {r}	Вершин {q, r}	Плот- ность[англ.]	χ	Группа симметрии	Двойственный {r, q,p}
Икосаэдральный 120-ячейник[англ.] (огранённый Шестисотячейник)			{3,5,5/2}	120 {3,5}	1200 {3}	720 {5/2}	120 {5,5/2}	4	480	H4 [5,3,3]	Малый звёздчатый 120-ячейник
Малый звёздчатый 120-ячейник[англ.]			{5/2,5,3}	120 {5/2,5}	720 {5/2}	1200 {3}	120 {5,3}	4	−480	H4 [5,3,3]	Икосаэдральный 120-ячейник
Большой 120-ячейник[англ.]			{5,5/2,5}	120 {5,5/2}	720 {5}	720 {5}	120 {5/2,5}	6	0	H4 [5,3,3]	Самодвойственный
Великий 120-ячейник[англ.]			{5,3,5/2}	120 {5,3}	720 {5}	720 {5/2}	120 {3,5/2}	20	0	H4 [5,3,3]	Большой звёздчатый 120-ячейник
Большой звёздчатый 120-ячейник[англ.]			{5/2,3,5}	120 {5/2,3}	720 {5/2}	720 {5}	120 {3,5}	20	0	H4 [5,3,3]	Великий 120-ячейник
Великий звёздчатый 120-ячейник[англ.]			{5/2,5,5/2}	120 {5/2,5}	720 {5/2}	720 {5/2}	120 {5,5/2}	66	0	H4 [5,3,3]	Самодвойственный
Большой великий 120-ячейник[англ.]			{5,5/2,3}	120 {5,5/2}	720 {5}	1200 {3}	120 {5/2,3}	76	−480	H4 [5,3,3]	Большой икосаэдральный 120-ячейник
Большой икосаэдральный 120-ячейник[англ.] (большой огранёный 600-ячейник)			{3,5/2,5}	120 {3,5/2}	1200 {3}	720 {5}	120 {5/2,5}	76	480	H4 [5,3,3]	Великий большой 120-ячейник
Великий 600-ячейник[англ.]			{3,3,5/2}	600 {3,3}	1200 {3}	720 {5/2}	120 {3,5/2}	191	0	H4 [5,3,3]	Великий большой звёздчатый 120-ячейник
Большой великий 120-ячейник[англ.]			{5/2,3,3}	120 {5/2,3}	720 {5/2}	1200 {3}	600 {3,3}	191	0	H4 [5,3,3]	Великий 600-ячейник

Существует 4 несостоявшихся правильных звёздчатых перестановок многогранников: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5/2}. Их ячейки и вершинные фигуры существует, но они не покрывают гиперсферу конечным числом представлений.

В пятимерном пространстве^[англ.] правильные многогранники можно обозначить как ${\displaystyle \{p,q,r,s\}}$, где ${\displaystyle \{p,q,r\}}$ является типом 4-грани, ${\displaystyle \{p,q\}}$ является типом ячейки, ${\displaystyle \{p\}}$ является типом 2-грани, ${\displaystyle \{s\}}$ является фигурой грани, ${\displaystyle \{r,s\}}$ является рёберной фигурой, а ${\displaystyle \{q,r,s\}}$ является вершинной фигурой.

Вершинная фигура (5-мерного многогранника) является 4-мерным многогранником, образованным вершинами, соседними с данной вершиной.

Рёберная фигура^[англ.] (5-мерного многогранника) является многогранником, образованным гранями вокруг каждого ребра.

Фигура грани^[англ.] (5-мерного многогранника) является многогранником, образованным ячейками вокруг каждой грани.

Правильный 5-мерный многогранник ${\displaystyle \{p,q,r,s\}}$ существует, только если ${\displaystyle \{p,q,r\}}$ и ${\displaystyle \{q,r,s\}}$ являются правильными четырёхмерными многогранниками.

В зависимости от значения

${\displaystyle {\frac {\cos ^{2}\left({\frac {\pi }{q}}\right)}{\sin ^{2}\left({\frac {\pi }{p}}\right)}}+{\frac {\cos ^{2}\left({\frac {\pi }{r}}\right)}{\sin ^{2}\left({\frac {\pi }{s}}\right)}}}$

получим тип пространства

${\displaystyle <1}$: Сферическое 4-мерное замощение или 5-мерный многогранник

${\displaystyle =1}$: евклидово 4-мерное замощение

${\displaystyle >1}$: Гиперболическое 4-мерное замощение

Из этих ограничений получаем 3 выпуклых многогранника, нуль невыпуклых многогранников, 3 4-мерных замощения и 5 гиперболических 4-мерных замощений. Не существует невыпуклых правильных многогранников в пятимерном пространстве и выше.

В размерностях 5 и выше существует только три вида выпуклых правильных многогранников ^[10].

Название	Символ Шлефли {p1,...,pn−1}	Коксетер	k-граней	Тип фасеты	Вершинная фигура	Двойственный
n-симплекс	{3n−1}	...	${\displaystyle {{n+1} \choose {k+1}}}$	{3n−2}	{3n−2}	Самодвойственен
n-куб	{4,3n−2}	...	${\displaystyle 2^{n-k}{n \choose k}}$	{4,3n−3}	{3n−2}	n-ортоплекс
n-ортоплекс	{3n−2,4}	...	${\displaystyle 2^{k+1}{n \choose {k+1}}}$	{3n−2}	{3n−3,4}	n-куб

Существуют также несобственные случаи, в которых некоторые числа в символе Шлефли равны 2. Например, {p,q,r,...2} является несобственным правильным сферическим многогранником в случае, если {p,q,r...} является правильным сферическим многогранником, и {2,...p,q,r} является несобственным правильным сферическим многогранником, когда {...p,q,r} является правильным сферическим многогранником. Такие многогранники можно использовать как фасеты, дающие формы вида {p,q,...2...y,z}.

Название	Символ Шлефли {p,q,r,s} Коксетер	Число фасет (четырёхмерных граней) {p,q,r}	Ячеек (трёхмерных граней) {p,q}	Граней (двумерных) {p}	Рёбер	Вершин	Фигура при грани {s}	Рёберная фигура {r,s}	Вершинная фигура {q,r,s}
Гексатерон	{3,3,3,3}	6 {3,3,3}	15 {3,3}	20 {3}	15	6	{3}	{3,3}	{3,3,3}
Пентеракт	{4,3,3,3}	10 {4,3,3}	40 {4,3}	80 {4}	80	32	{3}	{3,3}	{3,3,3}
5-ортоплекс	{3,3,3,4}	32 {3,3,3}	80 {3,3}	80 {3}	40	10	{4}	{3,4}	{3,3,4}

Гексатерон

Пентеракт

5-ортоплекс

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	χ
6-симплекс[англ.]	{3,3,3,3,3}	7	21	35	35	21	7	0
Хексеракт	{4,3,3,3,3}	64	192	240	160	60	12	0
6-ортоплекс[англ.]	{3,3,3,3,4}	12	60	160	240	192	64	0

6-мерный симплекс[англ.]

Хексеракт

6-мерный ортоплекс[англ.]

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	χ
7-симплекс[англ.]	{3,3,3,3,3,3}	8	28	56	70	56	28	8	2
Хептеракт	{4,3,3,3,3,3}	128	448	672	560	280	84	14	2
7-ортоплекс[англ.]	{3,3,3,3,3,4}	14	84	280	560	672	448	128	2

7-симплекс[англ.]

Хептеракт

7-ортоплекс[англ.]

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	7D-граней	χ
8-симплекс[англ.]	{3,3,3,3,3,3,3}	9	36	84	126	126	84	36	9	0
Октеракт	{4,3,3,3,3,3,3}	256	1024	1792	1792	1120	448	112	16	0
8-ортоплекс[англ.]	{3,3,3,3,3,3,4}	16	112	448	1120	1792	1792	1024	256	0

8-симплекс[англ.]

Октеракт

8-ортоплекс[англ.]

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	7D-граней	8D-граней	χ
9-симплекс[англ.]	{38}	10	45	120	210	252	210	120	45	10	2
Энтенеракт	{4,37}	512	2304	4608	5376	4032	2016	672	144	18	2
9-ортоплекс[англ.]	{37,4}	18	144	672	2016	4032	5376	4608	2304	512	2

9-симплекс[англ.]

Энтенеракт

9-ортоплекс[англ.]

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	7D-граней	8D-граней	9D-граней	χ
10-симплекс[англ.]	{39}	11	55	165	330	462	462	330	165	55	11	0
Декеракт	{4,38}	1024	5120	11520	15360	13440	8064	3360	960	180	20	0
10-ортоплекс[англ.]	{38,4}	20	180	960	3360	8064	13440	15360	11520	5120	1024	0

10-симплекс[англ.]

Декеракт

10-ортоплекс[англ.]

...

Не существует невыпуклых правильных многогранников в размерностях 5 и выше.

Проективный правильный (n+1)-многогранник существует, если исходное правильное n-сферическое замощение {p,q,...} центрально симметрично. Такие многогранники называются полу-{p,q,...}, и содержат вполовину меньше элементов. Коксетер даёт им символ {p,q,...}/2, в то время как Макмуллен пишет {p,q,...}_h/2, где h — число Кокстера. ^[11]

Правильные многоугольники с чётным числом сторон имеют полу-2n-угольные проективные многоугольники, {2p}/2.

Существует 4 правильных проективных многогранника^[англ.], соответствующих 4 из 5 платоновых тел.

Полукуб и полуоктаэдр обобщаются в полу-n-кубы и полу-n-ортоплексы в любой размерности.

3-dimensional regular hemi-polytopes

Название	Коксетер McMullen	Image	Faces	Edges	Vertices	χ
Полукуб[англ.]	{4,3}/2 {4,3}3		3	6	4	1
Полуоктаэдр[англ.]	{3,4}/2 {3,4}3		4	6	3	1
Полудодекаэдр	{5,3}/2 {5,3}5		6	15	10	1
Полуикосаэдр	{3,5}/2 {3,5}5		10	15	6	1

В 4-мерном пространстве 5 из 6 выпуклых правильных многогранников образуют проективные 4-мерные многогранники. 3 специальных случая — это полудвадцатичетырёхъячейник, полушестисотъячейник и полустодвадцатиячейник.

4-мерные правильные полумногогранники!Название

Символ
Коксетера

Символ
Макмаллена

Ячеек

Граней

Рёбер

Вершин

χ

полутессеракт	{4,3,3}/2	{4,3,3}4	4	12	16	8	0
полушестнадцатиячейник	{3,3,4}/2	{3,3,4}4	8	16	12	4	0
полудвадцатичетырёхъячейник	{3,4,3}/2	{3,4,3}6	12	48	48	12	0
полустодвадцатиячейник	{5,3,3}/2	{5,3,3}15	60	360	600	300	0
полушестисотъячейник	{3,3,5}/2	{3,3,5}15	300	600	360	60	0

Существует только 2 выпуклых правильных проективных полумногогранника в пространствах размерности 5 и выше.

Название	Шлефли	4D-граней	Ячеек (3D)	Граней (2D)	Рёбер	Вершин	χ
полупентеракт	{4,3,3,3}/2	5	20	40	40	16	1
полупентакросс[англ.]	{3,3,3,4}/2	16	40	40	20	5	1

Бесконечногранник^[англ.] — это многогранник, имеющий бесконечное число фасет. n-бесконечногранник — это n-мерный бесконечногранник: 2-бесконечногранник = бесконечноугольник (апейрогон), 3-бесконечногранник = бесконечногранник в трёхмерном пространстве и т.д.

Существует два главных геометрических класса бесконечногранников:^[12]

• Правильные соты в n-мерном пространстве, полностью заполняющие n-мерное пространство.
• Правильные косые бесконечногранники^[англ.], содержащие n-мерные многообразия в более высоких пространствах.

Прямой апейрогон — это правильное замощение прямой с разделением её на бесконечно много равных отрезков. Он имеет бесконечно много вершин и рёбер. Его символ Шлефли равен {∞}, а диаграмма Коксетера — .

......

Апейрогоны на гиперболической плоскости, среди которых наиболее заметен правильный апейрогон {∞}, могут иметь кривизну, наподобие конечных многоугольников на евклидовой плоскости, и иметь вершины, лежащие на орициклах или гиперциклах.

Правильные апейрогоны со сходимостью на бесконечности имеют символ {∞} и существуют на орициклах, хотя в общем случае они могут существовать на гиперциклах.

{∞}	{πi/λ}
Бесконечноугольник на орицикле	Бесконечноугольник на гиперцикле

Выше показаны два гиперболических апейрогона на диске Пуанкаре. На правом рисунке показаны перпендикулярные прямые, разделяющие фундаментальные области, отстоящие на расстояние λ друг от друга.

Косые апейрогоны в двумерном пространстве (плоскости) образуют зигзаг. Если зигзаг симметричен и однороден, апейрогон правильный.

Косые апейрогоны можно построить в пространстве любой размерности. В трёхмерном пространстве косые апейрогоны^[англ.] образуют спираль и могут быть левыми или правыми.

Двумерное пространство	Трёхмерное пространство
Апейрогон в виде зигзага	Спиральный апейрогон

Существует три правильных замощения плоскости. Все три имеют эйлерову характеристику (χ) 0.

Название	Квадратная мозаика (кадриль)	Треугольная мозаика (дельтаплитка)	Шестиугольный паркет (гексаплитка)
Симметрия	p4m, [4,4], (*442)	p6m, [6,3], (*632)
Шлефли {p,q}	{4,4}	{3,6}	{6,3}
Диаграмма Коксетера
Рисунок

Существует две несобственные правильные мозаики — {∞,2}, бесконечноугольный диэдр, полученный из двух апейрогонов, каждый из которых заполняет полуплоскость, и двойственная ей {2,∞} мозаика, бесконечноугольный осоэдр, который можно представить как бесконечное число параллельных прямых.

{∞,2}[англ.],

{2,∞}[англ.],

Не существует правильных замощений плоскости звёздчатыми многоугольниками. Существует бесконечно много пар чисел, для которых выполняется условие плоской мозаики (1/p + 1/q = 1/2), например, {8/3,8}, {10/3,5}, {5/2,10}, {12/5,12}, и т.д., но ни одна из этих звёзд не подходит для замощения.

Замощения гиперболического двухмерного пространства — это гиперболические мозаики^[англ.]. Существует бесконечно много правильных мозаик в H². Как констатировано выше, любая положительная пара {p,q}, такая что 1/p + 1/q < 1/2 даёт гиперболическую мозаику. Фактически для общего треугольника Шварца (p, q, r) то же самое верно для 1/p + 1/q + 1/r < 1.

Существует много различных путей представления гиперболической плоскости, включая дисковую модель Пуанкаре, в которой плоскость отображается в диск, как показано ниже. Следует рассматривать все многоугольные грани замощения как равносторонние, и многоугольники становятся меньше при приближению к краю диска вследствие применения проекции, что похоже на эффект фотокамеры c объективом «Рыбий глаз».

Существует бесконечно много плоских правильных 3-бесконечногранников как правильных мозаик гиперболической плоскости, имеющих вид {p,q}, где p+q<pq/2.

• {3,7}, {3,8}, {3,9} ... {3,∞}
• {4,5}, {4,6}, {4,7} ... {4,∞}
• {5,4}, {5,5}, {5,6} ... {5,∞}
• {6,4}, {6,5}, {6,6} ... {6,∞}
• {7,3}, {7,4}, {7,5} ... {7,∞}
• {8,3}, {8,4}, {8,5} ... {8,∞}
• {9,3}, {9,4}, {9,5} ... {9,∞}
• ...
• {∞,3}, {∞,4}, {∞,5} ... {∞,∞}

Примеры:

Сферические (Платоновы)/Евклидовы/гиперболические (диск Пуанкаре: компактные/паракомпактные/некомпактные) замощения с их символами Шлефли
p \ q	3	4	5	6	7	8	...	∞	...	iπ/λ
3	(тетраэдр) {3,3}	(октаэдр) {3,4}	(икосаэдр) {3,5}	(дельта-плитка) {3,6}	{3,7}	{3,8}		{3,∞}