Центральність — Вікіпедія

Наука про мережі
Теорія
Граф Складні мережі Світ тісний Безмасштабна мережа Перколяція Структура спільноти Еволюція[en] Керованість[en] Візуалізація графів Соціальний капітал Аналіз зв’язків Оптимізація Транзитивність Теорія балансу Ефект мережі Соціальний вплив
Види мереж
Інформаційна (комп'ютерна) Телекомунікаційна Транспортна Соціальна аналіз Біологічна[en] Штучна нейронна мережа Семантична Просторова Залежностей[en] Потокова
Графи
Властивості Кліка Компонент Розріз Цикл Структура даних Ребро Петля Окіл Шлях Вершина Список суміжності[en] / матриця Список інцидентності / матриця Види Двочастковий Повний Орієнтований Гіперграф Мультиграф Випадковий Зважений
Метрики[en] Алгоритми
Центральність Степінь Близькість[ru] PageRank Кластеризація Асортативність[en] Відстань Модулярність[en] Ефективність[en]
Моделі
Топологія Випадковий граф Модель Ердеша — Реньї Модель Барабаші — Альберт Модель Воттса — Строгаца Гіперболічна (HGN)[en] Ієрархічна[en] Стохастична блокова модель Динаміка Булева мережа Агентне моделювання Епідемічні/SIR
Списки Категорії
Категорія:Теорія мереж Категорія:Теорія графів
п о р

Показники центральності або близькості до центру в теорії графів та аналізі мереж визначають найважливіші вершини графа. Їх використовують для виявлення найвпливовішої особи (осіб) у соціальній мережі, ключових вузлів інфраструктури в інтернеті або міських мережах і розносників хвороби. Концепції центральності спочатку розвивалися в аналізі соціальних мереж і багато термінів центральності використовуються для вимірювання соціологічних першоджерел^[2]. Не слід плутати ці показники з метриками впливу вузлів^[en], які шукають кількісні характеристики впливу кожного з вузлів у мережі.

Визначення та опис центральності[ред. | ред. код]

Показники центральності є відповідями на питання «Що характеризує важливість вершини?». Відповідь дається в термінах дійснозначної функції на вершинах графа, значення якої (як очікується) забезпечують ранжування, яке визначає найважливіші вузли^[3][4][5].

Слово «важливість» має широкий спектр значень, що призводить до багатьох різних визначень центральності. Запропоновано дві схеми категоризації. «Важливість» можна розглядати стосовно типу потоку або передавання даних через мережу. Це дозволяє класифікувати центральності за типом потоку, який вважається важливим^[4]. З іншого боку, «важливість» можна пов'язати зі впливом на цілісність мережі. Це дозволяє класифікувати центральності на основі того, як вони вимірюють внесок у згуртованість мережі^[6]. Обидва ці підходи поділяють центральності на різні категорії. Центральність, яка придатна для однієї категорії, часто буває непридатною, коли застосовується до іншої категорії^[4].

Якщо центральності категоризуються за їх участю, стає зрозуміло що більшість центральностей належать до однієї категорії. Кількість маршрутів, що починаються з даного вузла, відрізняється лише тим, яким чином маршрути визначаються і підраховуються. Обмеження домовленостей для цієї групи дозволяє опис центральностей на спектрі маршрутів від довжини один (центральність за степенем) до необмежених маршрутів (центральність за впливовістю)^[3][7]. Спостереження, що багато центральностей поділяють ці зв'язки, пояснює високий рівень кореляції між цими показниками.

Опис потоками в мережі[ред. | ред. код]

Мережу можна вважати описом шляхів, якими щось тече. Це дозволяє опис на основі типів потоків і типів шляхів, закодованих центральністю. Потік може бути заснований на перенесенні, де кожен неподільний елемент проходить від одного вузла до іншого подібно до доставки пакунків з поштового відділення до будинку клієнта. В іншому випадку, проходячи в наступний вузол елемент розмножується, так що і джерело, і ціль містять цей елемент. Прикладом такого випадку є поширення чуток, коли інформація поширюється приватно, при цьому в кінці процесу і джерело, і ціль виявляються поінформованими. Останнім випадком є паралельне розмноження, коли елемент розмножується за кількома зв'язками одночасно на зразок трансляції по радіо, що забезпечує надходження тієї самої інформації багатьом слухачам одночасно^[4].

Аналогічно, вид шляху можна обмежити: геодезичними (найкоротші шляхи), шляхами (жодна вершина не відвідується більше одного разу), ланцюгами (вершини можуть відвідуватися по кілька разів, але по жодному ребру не проходять двічі) або маршрутами (і вершини, і ребра можуть зустрітися кілька разів) ^[4].

Опис за структурою обходів[ред. | ред. код]

Іншу класифікацію можна отримати зі способу побудови центральності. Це знову призводить до розбиття на два класи — радіальні або медіанні. Радіальні центральності підраховують кількість маршрутів, що починаються/закінчуються в даній вершині. Центральність за степенем і центральність за впливовістю є прикладами радіальних показників центральності, підраховуючи число маршрутів довжини один або необмеженої довжини. Медіанні центральності підраховують маршрути, які проходять через дану вершину. Канонічним прикладом є центральність за посередництвом Фрімана — кількість найкоротших маршрутів, які проходять через дану вершину^[6].

Аналогічно, підрахунок може захоплювати або обсяг, або довжину маршруту. Обсяг — це повне число маршрутів даного типу. Три приклади з попереднього абзацу потрапляють у цю категорію. Довжина — це відстань від цієї вершини до інших вершин графа. Центральність за близькістю до інших вузлів Фрімана, повна геодезична відстань від цієї вершини до всіх інших вершин є найвідомішим прикладом^[6]. Зауважте, що ця класифікація залежить від типу підраховуваних маршрутів (тобто маршрути, ланцюги, шляхи чи геодезичні).

Боргатті і Еверетт висловили думку, що ця типологія дає уявлення, як порівнювати міри центральності. Центральності, що потрапляють в ту саму комірку в цій 2×2 класифікації, досить схожі, щоб бути прийнятними альтернативами, і можна обґрунтовано порівнювати, який показник кращий для даної задачі. Міри з різних комірок, однак, абсолютно різні. Будь-яке визначення відносної придатності може відбуватися тільки у визначеному контексті, яка категорія більш придатна і що робить порівняння неможливим^[6].

Радіально-об'ємні центральності, що існують на спектрі[ред. | ред. код]

Опис структурою маршруту показує, що майже всі вживані центральності є радіально-об'ємними мірами. Це наштовхує на думку, що центральність вершини є функцією центральності вершин, з якими вона асоційована. Центральності відрізняються способом асоціації.

Боначич показав, що якщо асоціація визначена в термінах маршрутів, то сімейство центральностей можна визначити на основі розглянутих довжин маршрутів^[3]. Центральність за степенем підраховує кількість маршрутів завдовжки одиниця, центральність за впливовістю підраховує маршрути необмеженої довжини. Можливі також альтернативні визначення асоціацій. Альфа-центральність^[en] дозволяє вершинам мати зовнішні джерела впливу. Центральність Естради за підграфами підраховує тільки замкнуті шляхи (трикутники, чотирикутники тощо).

Основою таких мір є спостереження, що матриці суміжності графа дають число маршрутів з довжиною, рівною мірі. Аналогічно, експонента матриці тісно пов'язана з числом маршрутів заданої довжини. Початкове перетворення матриці суміжності дозволяє різні визначення підрахунку типів маршрутів. За будь-якого підходу центральність вершини можна виразити як нескінченну суму, або

${\displaystyle \sum _{k=0}^{\infty }A_{R}^{k}\beta ^{k}}$

для степенів матриці, або

${\displaystyle \sum _{k=0}^{\infty }{\frac {(A_{R}\beta )^{k}}{k!}}}$

для експонент матриці, де

• ${\displaystyle k}$ дорівнює довжині маршруту,
• ${\displaystyle A_{R}}$ є перетвореною матрицею суміжності, а
• ${\displaystyle \beta }$ є компенсаційним параметром, що забезпечує збіжність суми.

Сімейство мір Боначича не перетворює матрицю суміжності. Альфа-центральність^[en] замінює матрицю суміжності її резольвентою. Центральність підграфа замінює матрицю суміжності її слідом. Незалежно від початкового перетворення матриці суміжності всі ці підходи мають спільну обмежувальну поведінку. За прямування ${\displaystyle \beta }$ до нуля показник збігається до центральності за степенем. За прямування ${\displaystyle \beta }$ до найбільшого значення показник збігається до центральності за впливовістю^[7].

Теоретико-ігрова центральність[ред. | ред. код]

Загальна властивість більшості згаданих вище стандартних заходів полягає в тому, що вони оцінюють важливість вузла, фокусуючись лише на ролі, яку вузол відіграє сам по собі. Однак у багатьох застосуваннях такий підхід не є адекватним, оскільки, застосовуючи міри до груп вузлів, слід врахувати взаємодію вузлів.

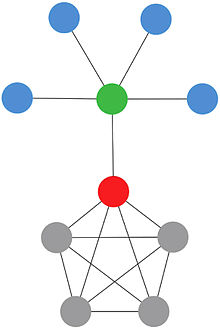
Наприклад, розглянемо задачу зупинки епідемії. Перегляньмо наведене зображення мережі: які вузли слід вакцинувати? Спираючись на описані вище міри, ми хочемо розпізнати вузли, які найважливіші в поширенні хвороби. Використання підходів, заснованих на центральностях, які фокусуються на індивідуальних властивостях вузлів, виявитись поганою ідеєю. Вузли в червоному прямокутнику окремо не можуть зупинити поширення хвороби, але при розгляді їх як групи ми ясно бачимо, що вони можуть зупинити хворобу, якщо вона починається у вузлах ${\displaystyle v_{1}}$,${\displaystyle v_{4}}$,${\displaystyle v_{5}}$. Теоретико-ігрові центральності намагаються взяти до уваги описані проблеми і можливості, використовуючи засоби теорії ігор. Підхід, запропонований у статті Михаляка (зі співавторами)^[8], використовує вектор Шеплі. Зважаючи на складність обчислення (за часом) вектора Шеплі більша частина зусиль у цій галузі вкладається в розробку нових алгоритмів і методів, які спираються на конкретну топологію мережі і особливий характер завдання. Такий підхід може скоротити часову складність алгоритму з експоненціальної до поліноміальної.

Важливі обмеження[ред. | ред. код]

Показники центральності мають два важливих обмеження, одне з яких очевидне, інше ж ледь уловиме. Очевидне обмеження полягає в тому, що центральність, яка оптимальна для одного застосування, часто не оптимальна для іншого. Більш того, якщо б це було не так, не треба було б стільки різних центральностей. Ілюстрацію цього феномена дає повітряний змій Крекгарда, для якого три різних поняття центральності дають три різних найбільш центральних вершини^[9].

Слабко вловиме обмеження полягає в тому, що має місце повсюдна омана: центральність вершини відбиває відносну важливість вершин. показники центральності розроблялися явно для ранжування, що дозволяє виділяти найважливіші вершини^[3][4]. Вони роблять це добре за згаданих обмежень. Вони не розроблялися для вимірювання вузлів у загальному вигляді. Нещодавно фізики, які працюють у галузі мереж, почали розробляти метрики впливу вузлів^[en] для розв'зання цієї задачі.

Помилка двояка. По-перше, ранжування тільки за порядком вершин як їх важливістю не відбиває різниці важливостей між різними рівнями ранжування. Цей факт можна пом'якшити, застосувавши центральності Фрімана до розглянутої міри центральності, що дає деяке розуміння важливості вузлів за їхніми різними кількісними показниками центральності. Більш того, центральність Фрімана дозволяє порівняти деякі мережі за показниками вузлів з найбільшими значеннями^[10].

По-друге, властивості, які (правильно) відбивають найважливіші вершини в даній мережі/застосуванні, не обов'язково узагальнюються на інші вершини. Для більшості інших вузлів мережі ранжування може виявитися безглуздим^{[11][12][13][14]}. Це пояснює, наприклад, чому тільки перші кілька результатів пошуку зображення в Google з'являються в адекватному порядку. PageRank є вкрай нестабільною мірою, демонструючи часто протилежний ранг після невеликої зміни параметра пошуку^[15].

Хоча неможливість узагальнення показника центральності на іншу мережу може здатися на перший погляд неочевидною, вона випливає прямо з наведених вище визначень. Складні мережі мають неоднорідну топологію. Наскільки оптимальна міра залежить від мережевої структури найважливіших вершин, настільки ж міра, оптимальна для таких вершин, не є оптимальною для решти мережі^[11].

Центральність за степенем[ред. | ред. код]

Історично першим і концептуально найпростішим поняттям є центральність за степенем, який визначається як число зв'язків, інцидентних вузлу (тобто число зв'язків, які має вузол). Степінь можна інтерпретувати в термінах прямого ризику вузла підхопити щось, що проходить через мережу (наприклад, вірус або якусь інформацію). У разі орієнтованої мережі (де зв'язки мають напрям) зазвичай визначають дві різні міри центральності за степенем, а саме, напівстепінь входу і напівстепінь виходу. Відповідно, напівстепінь входу — це число зв'язків з вузлом, а напівстепінь виходу — це число зв'язків вузла з іншими вузлами. Коли зв'язок асоціюється з деяким позитивним аспектом, таким як дружба чи співпраця, напівстепінь входу часто інтерпретується як вид популярності, а напівстепінь виходу як товариськість.

Центральність за степенем вершини ${\displaystyle v}$ цього графа ${\displaystyle G:=(V,E)}$ з ${\displaystyle |V|}$ вершинами і ${\displaystyle |E|}$ ребрами, визначається як

${\displaystyle C_{D}(v)=\deg(v)}$

Обчислення центральності за степенем для всіх вузлів у графі займає час ${\displaystyle \Theta (V^{2})}$ в поданні графа у вигляді щільної матриці суміжності, а для ребер займає час ${\displaystyle \Theta (E)}$ в поданні з розрідженою матрицею.

Визначення центральності за рівнем вузла можна поширити на весь граф і в цьому випадку ми говоримо про центральність графа^[10]. Нехай ${\displaystyle v*}$ буде вузлом з найвищою центральністю за степенем у ${\displaystyle G}$. Нехай ${\displaystyle X:=(Y,Z)}$ буде зв'язним графом з ${\displaystyle |Y|}$ вузлами, який максимізує таку величину (з ${\displaystyle y*}$ як вузлом з найвищою центральністю за степенем в ${\displaystyle X}$):

${\displaystyle H=\sum _{j=1}^{|Y|}[C_{D}(y*)-C_{D}(y_{j})]}$

Відповідно, центральність за степенем графа ${\displaystyle G}$ дорівнює:

${\displaystyle C_{D}(G)={\frac {\sum _{i=1}^{|V|}[C_{D}(v*)-C_{D}(v_{i})]}{H}}}$

Значення ${\displaystyle H}$ найбільше, коли граф ${\displaystyle X}$ містить один центральний вузол, з яким з'єднані всі інші вузли (граф-зірка), і в цьому випадку

${\displaystyle H=(n-1)\cdot ((n-1)-1)=n^{2}-3n+2.}$

Таким чином, для будь-якого графа ${\displaystyle G:=(V,E),}$

${\displaystyle C_{D}(G)={\frac {\sum _{i=1}^{|V|}[C_{D}(v*)-C_{D}(v_{i})]}{|V|^{2}-3|V|+2}}}$

Центральність за близькістю[ред. | ред. код]

У зв'язному графі нормалізований центральність за близькістю вузла дорівнює середній довжині найкоротшого шляху між вузлом і всіма іншими вузлами в графі. Тоді що центральніший вузол, то ближче він до решти вузлів.

Центральність за близькістю Алекс Бавелас^[en] (1950) визначив як величину, обернену до віддаленості^[16][17], тобто

${\displaystyle C(x)={\frac {1}{\sum _{y}d(y,x)}}}$,

де ${\displaystyle d(y,x)}$ дорівнює відстані між вершинами ${\displaystyle x}$ і ${\displaystyle y}$. Проте, коли кажуть про центральність за близькістю до інших вузлів, зазвичай мають на увазі його нормалізовану форму, що зазвичай отримується з попередньої формули множенням на ${\displaystyle N-1}$, де ${\displaystyle N}$ — число вузлів у графі. Нормалізація робить можливим порівняння між вузлами графів різного розміру.

Розгляд відстані з або у всі інші вузли незастосовний для неорієнтованих графів, тоді як в орієнтованих графах вони дають зовсім різні результати. Наприклад, інтернет-сайт може мати високу центральність за близькістю від вихідного з'єднання, але низьку центральність за близькістю від вхідних з'єднань.

Гармонічна центральність[ред. | ред. код]

В (необов'язково зв'язному) графі гармонічна центральність обертає операції підсумовування та обернення у визначенні центральності за близькістю:

${\displaystyle H(x)=\sum _{y\neq x}{\frac {1}{d(y,x)}}}$,

де ${\displaystyle 1/d(y,x)=0}$, якщо немає шляху з ${\displaystyle y}$ в ${\displaystyle x}$. Гармонічну центральність можна нормалізувати діленням на ${\displaystyle N-1}$, де ${\displaystyle N}$ — число вузлів у графі.

Гармонічну центральність запропонували Марчіорі і Латора^[en] (2000)^[18], потім, незалежно, Деккер (2005) під назвою «значуща центральність» (англ. valued centrality)^[19], і Рочат (2009)^[20].

Центральність за посередництвом[ред. | ред. код]

Центральність за посередництвом — це міра центральності вершини в графі (існує також центральність за посередництвом ребра, який тут не обговорюється). Центральність за посередництвом кількісно виражає число разів, коли вузол є мостом у найкоротшому шляху між двома іншими вузлами. Центральність за посередництвом увів Лінтон Фріман як міру кількісного вираження взаємодії людини з іншими людьми в соціальній мережі^[21]. У цій концепції вершини, що мають найбільшу ймовірність опинитися на випадково вибраному найкоротшому шляху між двома випадково вибраними вершинами, мають високу центральність за посередництвом.

Центральність за посередництвом вершини ${\displaystyle v}$ в графі ${\displaystyle G:=(V,E)}$ з ${\displaystyle V}$ вершинами обчислюється так:

1. Для кожної пари вершин (s,t) обчислюють найкоротші шляхи між ними.
2. Для кожної пари вершин (s,t) визначають частку найкоротших шляхів, які проходять через розглянуту вершину (тут, вершину v).
3. Підсумовують ці частки за всіма парами вершин (s,t).

Компактніше центральність за посередництвом можна подати як^[22]:

${\displaystyle C_{B}(v)=\sum _{s\neq v\neq t\in V}{\frac {\sigma _{st}(v)}{\sigma _{st}}}}$,

де ${\displaystyle \sigma _{st}}$ дорівнює загальному числу найкоротших шляхів від вузла ${\displaystyle s}$ до вузла ${\displaystyle t}$, а ${\displaystyle \sigma _{st}(v)}$ дорівнює числу таких шляхів, які проходять через ${\displaystyle v}$. Центральність за посередництвом можна нормалізувати шляхом ділення на число пар вершин, які не включають v, що для орієнтованих графів дорівнює ${\displaystyle (n-1)(n-2)}$, а для неорієнтованих графів дорівнює ${\displaystyle (n-1)(n-2)/2}$. Наприклад, в неорієнтованій зірці центральна вершина (яка міститься в будь-якому з можливих найкоротших шляхів) має центральність за посередництвом ${\displaystyle (n-1)(n-2)/2}$ (1, якщо нормалізувати), тоді як листки (які не містяться в жодному найкоротшому шляху) мають центральність за посередництвом 0.

З точки зору обчислень, як центральність за посередництвом, так і центральність за близькістю всіх вершин графа тягнуть за собою обчислення найкоротших шляхів між усіма парами вершин графа, що вимагає час ${\displaystyle O(V^{3})}$ за використання алгоритму Флойда — Воршелла. Однак на розріджених графах алгоритм Джонсона може виявитися ефективнішим, працюючи за час ${\displaystyle O(V^{2}\log V+VE)}$. У разі незважених графів обчислення можна виконати за допомогою алгоритму Брандеса^[22], який витрачає час ${\displaystyle O(VE)}$. Зазвичай ці алгоритми припускають, що графи не орієнтовані і зв'язні з дозволом петель і кратних ребер. Коли ж йдеться про мережеві графи, що зображають прості зв'язки, вони часто не мають петель або кратних ребер (де ребра зображають зв'язки між людьми або вершинами). У цьому випадку використання алгоритму Брандеса кінцевий показник центральності ділиться на 2, щоб урахувати, що кожен найкоротший шлях враховано двічі^[22].

Центральність за впливовістю[ред. | ред. код]

Центральність за впливовістю є мірою впливу вузла в мережі. Вона призначає відносні показники всім вузлам у мережі, ґрунтуючись на концепції, що зв'язки з вузлами з високим показником дають більший внесок у показник розглянутого вузла, ніж такий самий зв'язок з вузлом, що має низький показник^[23][5][5]. Показник PageRank компанії Google і центральність вузла за Кацом є варіантами центральності за впливовістю^[24].

Використання матриці суміжності для знаходження центральності за впливовістю[ред. | ред. код]

Для заданого графа ${\displaystyle G:=(V,E)}$ з ${\displaystyle |V|}$ вершинами нехай ${\displaystyle A=(a_{v,t})}$ — матриця суміжності, тобто ${\displaystyle a_{v,t}=1}$, якщо вершина ${\displaystyle v}$ зв'язана з вершиною ${\displaystyle t}$, і ${\displaystyle a_{v,t}=0}$ в іншому випадку. Відносний показник центральності вершини ${\displaystyle v}$ можна визначити як

${\displaystyle x_{v}={\frac {1}{\lambda }}\sum _{t\in M(v)}x_{t}={\frac {1}{\lambda }}\sum _{t\in G}a_{v,t}x_{t}}$,

де ${\displaystyle M(v)}$ — множина сусідів вершини ${\displaystyle v}$, а ${\displaystyle \lambda }$ — константа. Після невеликих перетворень цей вираз можна переписати у векторних позначеннях як рівняння для власного вектора

${\displaystyle \mathbf {Ax} ={\lambda }\mathbf {x} }$

В загальному випадку є багато різних власних значень ${\displaystyle \lambda }$, для яких існують ненульові власні вектори. Оскільки елементи матриці суміжності невід'ємні, існує єдине найбільше власне значення, яке дійсне і додатне, за теоремою Перрона — Фробеніуса. Це найбільше власне значення дає бажану міру центральності^[23]. Компонента ${\displaystyle v^{th}}$ зв'язаного власного вектора дає відносний показник центральності вершини ${\displaystyle v}$ у мережі. Власний вектор визначений з точністю до множника, так що цілком визначено тільки відношення центральностей вершин. Щоб визначити абсолютне значення показника, слід нормалізувати власний вектор, наприклад, так, щоб сума за всіма вершинами дорівнювала 1, або нормалізувати загальним числом вершин n. Степеневий метод є одним з багатьох алгоритмів отримання власних значень, який можна використати для знаходження цього домінівного власного вектора^[24]. Більш того, це можна узагальнити так, що елементи матриці A можуть бути дійсними числами, які вказують на силу зв'язку як у стохастичній матриці.

Центральність за Кацом[ред. | ред. код]

Центральність за Кацом^[25] є узагальненням центральності за степенем. Центральність за степенем вимірює кількість прямих сусідів, а центральність за Кацом вимірює кількість усіх вузлів, які можна пов'язати шляхами, при штрафування далеких вузлів. Математично ця центральність визначається як

${\displaystyle x_{i}=\sum _{k=1}^{\infty }\sum _{j=1}^{N}\alpha ^{k}(A^{k})_{ji}}$,

де ${\displaystyle \alpha }$ є коефіцієнтом ослаблення з інтервалу ${\displaystyle (0,1)}$.

Центральність за Кацом можна розглядати як варіант центральності за впливовістю. Іншою формою центральності за Кацом є

${\displaystyle x_{i}=\alpha \sum _{j=1}^{N}a_{ij}(x_{j}+1).}$

Порівняно із центральністю за впливовістю ${\displaystyle x_{j}}$ замінюється на ${\displaystyle x_{j}+1.}$

Показано^[26], що головний власний вектор (відповідний найбільшому власному значенню матриці суміжності ${\displaystyle A}$) є границею центральності за Кацом при прямуванні ${\displaystyle \alpha }$ до ${\displaystyle {\tfrac {1}{\lambda }}}$ знизу.

PageRank[ред. | ред. код]

PageRank задовольняє такій рівності

${\displaystyle x_{i}=\alpha \sum _{j}a_{ji}{\frac {x_{j}}{L(j)}}+{\frac {1-\alpha }{N}},}$

де

${\displaystyle L(j)=\sum _{i}a_{ji}}$

дорівнює числу сусідів вузла ${\displaystyle j}$ (або числу вихідних з'єднань орієнтованого графа). Порівняно із центральністю за впливовістю і центральністю за Кацом, важливою відмінністю є масштабний множник ${\displaystyle L(j)}$. Відмінність PageRank і центральності за впливовістю полягає в тому, що вектор PageRank є лівим власним вектором (тобто власним вектором транспонованої матриці, зауважте, що множника ${\displaystyle a_{ji}}$ має зворотний порядок індексів)^[27].

Центральність за протіканням[ред. | ред. код]

Існує багато мір центральності для виявлення «важливості» окремого вузла складної мережі. Однак, вони відбивають важливість вузла чисто в топологічних термінах і значення вузла ніяк не залежить від його «стану». Значення залишається сталим незалежно від динаміки мережі. Це справді так навіть для мір зваженого посередництва. Проте вузол може бути також центрально розташований у термінах центральності за посередництвом або іншої міри центральності, але не бути «центрально розташованим» у контексті мережі, в якій є протікання. Протікання «зарази» відбувається в складних мережах за великою кількістю сценаріїв. Вірусна або бактеріальна інфекція може поширюватися по соціальних мережах людей, відомих як мережі контактів. Поширення хвороби можна також розглядати на високому рівні абстракції, розглядаючи мережі міст або центрів зосередження людей, з'єднаних шосейними дорогами і залізницями або авіалініями. Комп'ютерні віруси можуть поширюватися комп'ютерними мережами. Чутки або новини про ділові пропозиції та угоди можуть також поширюватися між людьми через соціальні мережі. У всіх цих сценаріях «інфекція» поширюється через зв'язки складної мережі, змінюючи «стан» вузлів оборотно або необоротно. Наприклад, в епідеміологічному сценарії індивідууми переходять зі стану «вразливий» у стан «заражений». Стани конкретних вузлів у міру поширення «зарази» можуть набувати в наведених вище прикладах двійкових значень (таких як «порцію новин отримано/не отримано»), дискретних значень (сприйнятливий/заражений/вилікуваний), або навіть неперервних (таких як частка заражених людей у місті). Спільне для всіх цих сценаріїв те, що поширення «зарази» призводить до зміни стану вузлів мережі. Для врахування цього запропоновано центральність за протіканням (англ. Percolation centrality, PC), яка вимірює важливість вузла в термінах сприяння протіканню через мережу. Цю міру запропонували Пайравінан зі співавторами^[28].

Центральність за протіканням визначається для заданого вузла і в даний час пропорційно кількості «шляхів протікання», які проходять через вузол. «Шлях протікання» — це найкоротший шлях між парою вузлів, де вузол-джерело зазнав протікання (наприклад, заражений). Цільовий вузол може перебувати в стані просоченості, непросоченості або в стані часткової просоченості.

${\displaystyle PC^{t}(v)={\frac {1}{N-2}}\sum _{s\neq v\neq r}{\frac {\sigma _{sr}(v)}{\sigma _{sr}}}{\frac {{x^{t}}_{s}}{{\sum {[{x^{t}}_{i}}]}-{x^{t}}_{v}}}}$,

де ${\displaystyle \sigma _{sr}}$ — повне число найкоротших шляхів від вузла ${\displaystyle s}$ до вузла ${\displaystyle r}$, а ${\displaystyle \sigma _{sr}(v)}$ — число таких шляхів, що проходять через ${\displaystyle v}$. Стан просоченості вузла ${\displaystyle i}$ в момент ${\displaystyle t}$ позначається як ${\displaystyle {x^{t}}_{i}}$ і є два спеціальних випадки, коли ${\displaystyle {x^{t}}_{i}=0}$ що показує стан непротікання в момент ${\displaystyle t}$, і коли ${\displaystyle {x^{t}}_{i}=1}$, що свідчить про повне протікання в момент часу ${\displaystyle t}$. Значення між цими величинами означають стани часткового протікання (наприклад, у мережі міст це може бути відсоток заражених людей у місті).

Ваги шляхів протікання залежать від рівнів просоченості, призначених початковим вузлам, виходячи з постулату, що чим вищий рівень просоченості початкового вузла, тим важливіші шляхи, що виходять з цього вузла. Вузли, що лежать на найкоротших шляхах, які починаються у вузлах з високою просоченістю, потенційно важливіші для просочування. Визначення центральності за протіканням можна розширити, щоб включити також ваги цільових вузлів. Центральність за протіканням обчислюється за час ${\displaystyle O(NM)}$ за ефективної реалізації, запозиченої зі швидкого алгоритму Брандеса, а якщо при обчисленнях потрібно враховувати ваги кінцевих вузлів, час найгіршого випадку дорівнює ${\displaystyle O(N^{3})}$.

Кросклікова центральність[ред. | ред. код]

Кросклікова центральність окремого вузла в складному графі визначає зв'язки вузла з різними кліками. Вузол з високою кросокліковою центральністю сприяє поширенню інформації або хвороби в графі. Кліки — це підграфи, в яких кожен вузол з'єднаний з усіма іншими вузлами кліки. Кросклікова центральність вузла ${\displaystyle v}$ для даного графа ${\displaystyle G:=(V,E)}$ з ${\displaystyle |V|}$ вершинами і ${\displaystyle |E|}$ ребрами позначається як ${\displaystyle X(v)}$ і дорівнює числу клік, яким вершина ${\displaystyle v}$ належить. Цю міру використано в статті Фагані^[29], але вперше її запропонували Еверетт і Боргатті^[en] 1998 під назвою «центральність за перекриттям клік».

Централізованість Фрімана[ред. | ред. код]

Централізованість будь-якої мережі є мірою того, наскільки центральним є її найцентральніший вузол порівняно з іншими вузлами^[10]. Міра централізованості тоді (a) обчислюється як сума різниць центральності між центральним вузлом мережі і всіма іншими вузлами та (b) це значення ділиться на теоретично найбільшу таку суму різниць будь-якої мережі того ж розміру^[10]. Тоді будь-яка міра центральності може мати свою власну міру централізованості. Формально кажучи, якщо ${\displaystyle C_{x}(p_{i})}$ є мірою центральності точки ${\displaystyle i}$, якщо ${\displaystyle C_{x}(p_{*})}$ є найбільшою такою мірою в мережі і якщо

${\displaystyle \max \sum _{i=1}^{N}C_{x}(p_{*})-C_{x}(p_{i})}$

є найбільшою сумою різниць точкової центральності ${\displaystyle C_{x}}$ для будь-якого графа з тим самим числом вузлів, то централізованість мережі дорівнює^[10]

${\displaystyle C_{x}={\frac {\sum _{i=1}^{N}C_{x}(p_{*})-C_{x}(p_{i})}{\max \sum _{i=1}^{N}C_{x}(p_{*})-C_{x}(p_{i})}}.}$

Міри центральності, засновані на відмінностях[ред. | ред. код]

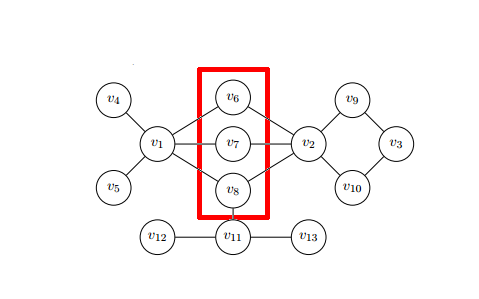
Щоб отримати найкращі результати в ранжуванні сайтів даної мережі, у статті Алвареза-Сокорро (зі співавторами)^[30] використовується міра несхожості (характерна для теорії класифікації й аналізу даних) для поліпшення міри центральності в складних мережах. Це ілюструє центральність за впливовістю, тобто обчислення центральності кожного вузла розв'язанням задачі знаходження власного значення

${\displaystyle W\mathbf {c} =\lambda \mathbf {c} }$,

де ${\displaystyle W_{ij}=A_{ij}D_{ij}}$ (покоординатний добуток), а ${\displaystyle D_{ij}}$ — довільна матриця несхожості, визначена через міру несхожості. Наприклад, через несхожість Жаккара, що задається формулою

${\displaystyle D_{ij}=1-{\dfrac {|V^{+}(i)\cap V^{+}(j)|}{|V^{+}(i)\cup V^{+}(j)|}}}$

Ця міра дозволяє виразити кількісно топологічний внесок (тому й називається центральністю за внеском) кожного вузла в центральність заданого вузла, отримуючи більше відношення вага/важливість цих вузлів з більшою несхожістю, оскільки це дозволяє заданому вузлу досягти вузлів, яких не можна досягти прямо.

Слід звернути увагу, що ${\displaystyle W}$ невід'ємна, оскільки ${\displaystyle A}$ і ${\displaystyle D}$ є неотрицательными матрицями, так що можна використати теорему Перрона — Фробеніуса, щоб забезпечити єдиність розв'язку задачі вище для ${\displaystyle \lambda =\lambda _{max}}$ з невід'ємним c, що дозволяє отримати центральність кожного вузла мережі. Таким чином, центральність i-го вузла дорівнює

${\displaystyle c_{i}={\dfrac {1}{n}}\sum _{j=1}^{n}W_{ij}c_{j},\,\,\,\,\,\,j=1,\cdots ,n}$,

де ${\displaystyle n}$ дорівнює числу вузлів мережі. Деякі мережі та міри несхожості випробувано в роботі Алвареза-Сокорро (зі співавторами)^[31] і в досліджуваних випадках одержано поліпшені результати.

Узагальнення[ред. | ред. код]

Емпіричні та теоретичні дослідження узагальнюють концепцію центральності в контексті статичних мереж на динамічну центральність^[32] в контексті залежних від часу і недовговічних мереж^[33][34][35].

Для узагальнення на зважені мережі див. статтю Опсала зі співавторами^[36].

Концепцію центральності узагальнено також на груповий рівень. Наприклад, ступінь групового посередництва показує пропорцію геодезичних зв'язків пар (тобто шляхів з мінімальною довжиною) вузлів, що не належать до групи, які проходять через групу^[37][38].

Див. також[ред. | ред. код]

• Альфа-центральність^[en]
• Модель «центр-периферія»^[en]
• Відстань у графах
• Центр графа

Примітки[ред. | ред. код]

Література[ред. | ред. код]

Література для подальшого читання[ред. | ред. код]

• Koschützki, D.; Lehmann, K. A.; Peeters, L.; Richter, S.; Tenfelde-Podehl, D. and Zlotowski, O. (2005) Centrality Indices. In Brandes, U. and Erlebach, T. (Eds.) Network Analysis: Methodological Foundations, pp.  16–61, LNCS 3418, Springer-Verlag.