分數傅立葉變換 - 维基百科，自由的百科全书

此條目已列出參考文獻，但因為沒有文內引註而使來源仍然不明。 (2018年9月23日) 请加上合适的文內引註来改善这篇条目。

在數學中，分數傅立葉變換（Fractional Fourier transform，縮寫：FRFT）指的就是傅立葉變換（Fourier Transform）的廣義化。近幾年來，分數傅立葉變換除了在信號處理領域有相當廣泛的應用，其也在數學上被單獨地研究，而定義出如分數迴旋積分（Fractional Convolution）、分數相關（Fractional Correlation）等許多相關的數學運算。

分數傅立葉變換的物理意義即做傅立葉變換 ${\displaystyle a}$ 次，其中 ${\displaystyle a}$ 不一定要為整數；而做了分數傅立葉變換之後，信號或輸入函數便會出現在介於時域與頻域之間的分數域（Fractional Domain）。

若再更進一步地廣義化分數傅立葉變換，則可推廣至線性標準變換。

對信號 ${\displaystyle x(t)}$ 做一次傅立葉變換的結果為${\displaystyle {\mathcal {F}}(x)}$ ，做兩次傅立葉變換的結果為${\displaystyle {\mathcal {F}}({\mathcal {F}}(x))}$ ，表示成${\displaystyle {\mathcal {F}}^{2}={\mathcal {F}}({\mathcal {F}}(x))}$ ，而當做了 ${\displaystyle a}$ 次的傅立葉變換可以寫成一般式 ${\displaystyle {\mathcal {F}}^{a}(x)={\mathcal {F}}^{(a-1)}({\mathcal {F}}(x))}$ 。至此，都以 ${\displaystyle a}$為整數做考量，當令 ${\displaystyle a={\frac {2\phi }{\pi }}}$ 即 ${\displaystyle \phi ={\frac {1}{2}}a\pi }$ 時，將 ${\displaystyle x(t)}$ 的分數傅立葉變換定義為 ${\displaystyle {\mathcal {F}}_{\phi }(x)={\mathcal {F}}^{2\phi /\pi }(x)}$，其中 ${\displaystyle \phi }$ 可以不必為整數。

分數傅立葉變換這個概念，其實最早在西元1929年，N.Wiener就已提出，但是並沒有受到太多的矚目。過了約莫50年，V.Namias 在西元1980年重新提出（稱之為重發明）這個概念，但是一直到西元1994年，才有人真正把分數傅立葉變換用在信號處理上，此人為 L. B. Almeida。詳細歷史：1937年提出分數傅立葉變換的概念雛形; 1980年Namias較明確地提出分數傅立葉變換的數學表達式，並將其用於具有確定邊界條件的量子力學薛定諤方程的求解1987年Bride & Kerr 給出嚴格的數學定義以及性質1993年由德國的學者羅曼，土耳其的Ozaktas和以色列的Mendlovic等人首次將分數傅立葉變換概念引入光學並給出了相應的光學過程; Mendlovic＆Ozaktas：漸變折射率GRIN介質中光傳播。 A. W. Lohmann: 維格納分佈函數和以及透鏡實現，自由空間的光衍射。 1993年Ozaktas，羅曼，Mendlovic等人在光學中全面引入分數傅立葉變換; 1995年Shih提出了另外一種分數傅立葉變換的形式; 1997年劉樹田等人根據Shih的定義給出了廣義分數傅立葉變換，1999年劉樹田等人將分數傅立葉變換應用於圖像加密研究中; 2001年Ozaktas等人出版“分數傅立葉變換及其在光學和信號處理中應用”一書。

第一種定義:

${\displaystyle X_{\phi }(u)={\sqrt {1-jcot\phi }}\cdot e^{j\pi \cdot cot\phi \cdot u^{2}}\int _{-\infty }^{\infty }e^{-j2\pi \cdot csc\phi \cdot ut}e^{j\pi \cdot cot\phi \cdot t^{2}}x(t)dt}$

第二種定義:

${\displaystyle X_{\phi }(u)={\sqrt {\frac {1-jcot\phi }{2\pi }}}\cdot e^{j{\frac {cot\phi }{2}}\cdot u^{2}}\int _{-\infty }^{\infty }e^{-jcsc\phi \cdot ut}e^{j{\frac {cot\phi }{2}}\cdot t^{2}}x(t)dt}$

${\displaystyle \phi =0.5a\pi }$, ${\displaystyle a}$ 為實數。

當 ${\displaystyle a=1}$ 時 (亦即 ${\displaystyle \phi =0.5\pi }$ )，分數傅立葉變換就成了傅立葉變換。

${\displaystyle {\mathcal {F}}^{2}(f)={\mathcal {F}}({\mathcal {F}}(f))}$ ，則可推廣為${\displaystyle {\mathcal {F}}^{(n+1)}(f)={\mathcal {F}}({\mathcal {F}}^{n}(f))}$;依此類推，${\displaystyle {\mathcal {F}}^{-n}(F)}$表示${\displaystyle F(\omega )}$的${\displaystyle n}$次逆變換${\displaystyle {\mathcal {F}}^{-1}(F)}$。

而分數傅立葉變換將以上定義推廣至非整數次的${\displaystyle n={\frac {2\alpha }{\pi }}}$，且${\displaystyle \alpha }$為實數，表示為

${\displaystyle {\mathcal {F}}_{\alpha }(f)={\mathcal {F}}^{2\alpha /\pi }(f)}$，

當${\displaystyle n={\frac {2\alpha }{\pi }}}$是一個整數時則代表傅立葉轉換做${\displaystyle n}$次。

例如:

${\displaystyle n=1}$時相當於做一次傅立葉變換，如果在時頻分析(Time-Frequency Analysis)圖上，則是對訊號順時針轉90度

${\displaystyle n=2}$時相當於做兩次傅立葉變換，如果在時頻分析(Time-Frequency Analysis)圖上，則是對訊號順時針轉180度,${\displaystyle {\mathcal {F}}^{2}[x(t)]=x(-t)}$

${\displaystyle n=3}$時相當於做三次傅立葉變換，如果在時頻分析(Time-Frequency Analysis)圖上，則是對訊號順時針轉270度

${\displaystyle n=4}$時相當於做四次傅立葉變換，如果在時頻分析(Time-Frequency Analysis)圖上，則是對訊號順時針轉360度,${\displaystyle {\mathcal {F}}^{4}[x(t)]=x(t)}$

對於任一實數${\displaystyle \alpha }$，一個對${\displaystyle f}$函數做${\displaystyle \alpha }$角度分數傅立葉變換定義為

${\displaystyle {\mathcal {F}}_{\alpha }(f)(\omega )={\sqrt {\frac {1-i\cot(\alpha )}{2\pi }}}e^{i\cot(\alpha )\omega ^{2}/2}\int _{-\infty }^{\infty }e^{-i\csc(\alpha )\omega t+i\cot(\alpha )t^{2}/2}f(t)dt}$

並且具備以下特性

• 加法性(Additivity)

${\displaystyle {\mathcal {F}}_{\alpha +\beta }(f)={\mathcal {F}}_{\alpha }({\mathcal {F}}_{\beta }(f))={\mathcal {F}}_{\beta }({\mathcal {F}}_{\alpha }(f))}$。

• 線性(Linearity)

${\displaystyle {\mathcal {F}}_{\alpha }\left[\sum \nolimits _{k}b_{k}f_{k}(u)\right]=\sum \nolimits _{k}b_{k}{\mathcal {F}}_{\alpha }\left[f_{k}(u)\right]}$

• 整數傅立葉性質(Integer Orders)

若${\displaystyle \alpha ={\frac {k\pi }{2}}}$,其中${\displaystyle k}$為一整數則相當於做${\displaystyle k}$次傅立葉轉換；

當${\displaystyle \alpha ={\frac {\pi }{2}}}$時，這個定義就變成了連續傅立葉變換的定義 ，

當${\displaystyle {\displaystyle \alpha ={\frac {-\pi }{2}}}}$時，它就變成了連續傅立葉變換之逆變換的定義。

若${\displaystyle \alpha }$為${\displaystyle \pi }$的整數倍，則餘切函數和餘割函數不會收斂。

有一方法可解決此問題，就是取limit讓以上定義變成有一個狄拉克δ函數被積分的情況，使得

${\displaystyle {\mathcal {F}}_{\alpha }={\mathcal {F}}_{\frac {k\pi }{2}}={\mathcal {F}}^{k}=({\mathcal {F}})^{k}}$

• 反轉性質(Inverse)

${\displaystyle ({\mathcal {F}}_{\alpha })^{-1}={\mathcal {F}}_{-\alpha }}$

• 交換性(Commutativity)

${\displaystyle {\mathcal {F}}_{\alpha _{1}}{\mathcal {F}}_{\alpha _{2}}={\mathcal {F}}_{\alpha _{2}}{\mathcal {F}}_{\alpha _{1}}}$

• 結合律(Associativity)

${\displaystyle \left({\mathcal {F}}_{\alpha _{1}}{\mathcal {F}}_{\alpha _{2}}\right){\mathcal {F}}_{\alpha _{3}}={\mathcal {F}}_{\alpha _{1}}\left({\mathcal {F}}_{\alpha _{2}}{\mathcal {F}}_{\alpha _{3}}\right)}$

• 帕塞瓦爾定理(Parseval Theorem)

若從時頻分析圖上來看，代表的意義是在時頻分析上旋轉一角度後能量守恆

${\displaystyle \int f^{*}(u)g(u)du=\int f_{\alpha }^{*}(u)g_{\alpha }(u)du}$

${\displaystyle x(t)}$ 的分數傅立葉轉換 (${\displaystyle \phi }$)的時頻分布，等同於 ${\displaystyle x(t)}$ 的時頻分布(維格納分布,加伯轉換)順時針旋轉角度 ${\displaystyle \phi }$，用數學式子表示如下:

假設

(a) ${\displaystyle W_{x}(t,f)}$ 是 ${\displaystyle x(t)}$ 的維格納分布

(b) ${\displaystyle W_{X_{\phi }}(u,v)}$ 是 ${\displaystyle X_{\phi }(u)}$ 的維格納分布

(c) ${\displaystyle X_{\phi }(u)}$ 是 ${\displaystyle x(t)}$ 的分數傅立葉轉換

，則${\displaystyle W_{X_{\phi }}(u,v)=W_{x}(ucos(\phi )-vsin(\phi ),usin(\phi )+vcos(\phi ))}$

假設

(a) ${\displaystyle G_{x}(t,f)}$ 是 ${\displaystyle x(t)}$ 的加伯轉換

(b) ${\displaystyle G_{X_{\phi }}(u,v)}$ 是 ${\displaystyle X_{\phi }(u)}$ 的加伯轉換

(c) ${\displaystyle X_{\phi }(u)}$ 是 ${\displaystyle x(t)}$ 的分數傅立葉轉換

，則${\displaystyle G_{X_{\phi }}(u,v)=G_{x}(ucos(\phi )-vsin(\phi ),usin(\phi )+vcos(\phi ))}$

例子一:

對一個加伯轉換後的餘弦函數做不同角度的分數傅立葉轉換。如下圖

例子二:

對一個加伯轉換後的矩形函數做不同角度的分數傅立葉轉換。如下圖

可用分解信號和濾除雜訊；一般來說分為兩種，一種是在時域(Time domain)上，一種是在頻域(Frequency domain)上，

這邊利用分數傅立葉轉換使其在分數域當中濾波。

假設現在${\displaystyle x(t)}$是由兩個信號組成:

${\displaystyle x(t)=x_{1}(t)+x_{2}(t)}$，

${\displaystyle x_{1}(t)}$和${\displaystyle x_{2}(t)}$ 用數學表示分別如下:

${\displaystyle x_{1}(t)={\begin{cases}1,&{\mbox{if }}0<t<1{\mbox{ }}\\0,&{\mbox{otherwise }}{\mbox{ }}\end{cases}}}$

${\displaystyle x_{2}(t)={\begin{cases}1,&{\mbox{if }}8<t<10{\mbox{ }}\\0,&{\mbox{otherwise }}{\mbox{ }}\end{cases}}}$

${\displaystyle h(t)={\begin{cases}1,&{\mbox{if }}-2<t<2{\mbox{ }}\\0,&{\mbox{otherwise }}{\mbox{ }}\end{cases}}}$

由式子可以很明顯地看出，${\displaystyle x1(t),x2(t)}$兩信號是方波。

若要將這兩個信號分開，是非常簡單的一件事情，因為這兩個信號在時域上毫無重疊，便可以直接在時域上將這兩個信號分開。

則 ${\displaystyle x(t)}$ 乘上 ${\displaystyle h(t)}$ 時，${\displaystyle x_{1}(t)}$這個信號會被保留，${\displaystyle x_{2}(t)}$這個信號就被濾掉了。

此作法可成功將這兩個信號分開。

此種方法的限制為欲分解的信號必須在时域不能重疊，否則無法成功分解。

${\displaystyle x(t)=x_{1}(t)+x_{2}(t)}$，

${\displaystyle x_{1}(t)=sin(4\pi t)}$，${\displaystyle x_{2}(t)=cos(10\pi t)}$。

可以很明顯地看出${\displaystyle x_{1}(t)}$和${\displaystyle x_{2}(t)}$ 在時域上完全重疊，因此很難在時域分解這兩個信號。

此時，可以妥善利用傅立葉轉換將信號${\displaystyle x(t)}$轉到頻域，其在頻域的表示式如下所示:

${\displaystyle X(f)=X_{1}(f)+X_{2}(f)}$

${\displaystyle X_{1}(f)={\frac {\delta (f-2)-\delta (f+2)}{2}}}$

${\displaystyle X_{2}(f)={\frac {\delta (f-5)+\delta (f+5)}{2}}}$

由${\displaystyle X(f)}$可以很明顯地看出，若要將這兩個信號在頻域上分開，是非常簡單的一件事情，因為這兩個信號經過傅立葉轉換後，在頻域上完全沒有重疊。

假設 ${\displaystyle H(f)}$ 為一個低通濾波器(Low-pass Filter)

${\displaystyle H(f)={\begin{cases}1,&{\mbox{if }}-3<t<3{\mbox{ }}\\0,&{\mbox{otherwise }}{\mbox{ }}\end{cases}}}$

則 ${\displaystyle X(f)}$ 乘上 ${\displaystyle H(f)}$ 時，${\displaystyle X_{1}(f)}$ 會被保留，${\displaystyle X_{2}(f)}$ 就被濾掉了。

反之，若要保留 ${\displaystyle X_{2}(f)}$ 而濾掉 ${\displaystyle X_{1}(f)}$ ，則可以使用高通濾波器(High-pass Filter)。

這種把欲處理信號先轉換到頻域，再做分解的動作，是濾波器設計的常見方法之一。

欲分解的信號必須在頻域不能重疊，否則無法成功分解。

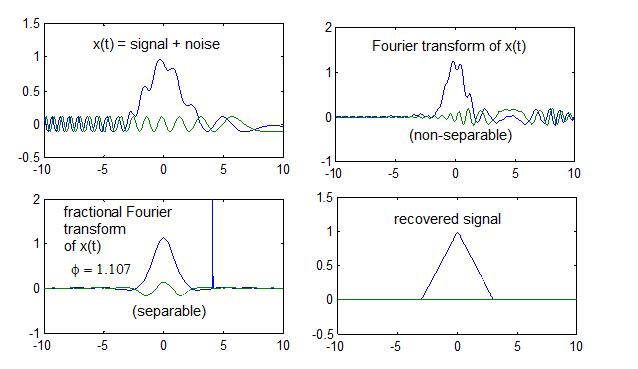
${\displaystyle x(t)=e^{j0.5(t-4)^{2}}}$ (啁啾雜訊) + 三角波信號。

三角波信號(藍色)是我們要的信號，將前面的啁啾(綠色)視為雜訊，由圖中可以發現到，

不論在時域或是頻域，皆無法直接將噪音項${\displaystyle e^{j0.5(t-4)^{2}}}$去除，這是因為${\displaystyle e^{j0.5(t-4)^{2}}}$和三角波信號在時域和頻域皆重疊(如下圖左上、右上)。

因此，對於兩個在時、頻域皆重疊的信號來說，很難在一維的時域和頻域中將其分解。

但若使用二維的時頻分析，則將有機會可以將兩個在時、頻域皆重疊的信號分解。

這是因為兩個在時、頻域皆重疊的信號其時頻分布並不一定會重疊。因此，只要這兩個信號的時頻分布沒有互相重疊，就可以善用分數傅立葉變換將其成功分解(如下圖左下、右下)。

假設有噪音干擾，所以接收到的信號除了原始信號以外，還包含了雜訊。

用時頻分析方法來處理接收到的信號，黑色為原始信號(signal)的時頻分布，而綠色為噪音(noise)的時頻分布，如下圖。

現在想把雜訊濾掉，以下探討3種方法來還原原始信號。

方法1 : 使用垂直的 Cutoff line

若在時頻分布圖中使用垂直的 Cutoff line ，就相當於在一維時域中，要把信號和噪音分離。

但是由下圖可清楚看出，使用垂直的 Cutoff line 後，仍然會有一部分的噪音無法被去除。

因此方法1無法完美重建原始信號，而會有扭曲的情形發生。

方法2 : 使用水平的 Cutoff line

若在時頻分布圖中使用水平的 Cutoff line ，就相當於在一維頻域中，要把信號和噪音分離。

但是由下圖可清楚看出，使用水平的 Cutoff line 後，仍然會有一部分的噪音無法被去除。

因此方法2也無法完美重建原始信號，而會有扭曲的情形發生。

方法3 : 使用斜的 Cutoff line

若在時頻分布圖中使用斜的 Cutoff line ，則可以完美分離信號和噪音。如下圖。

Cutoff line 的參數包含了 ${\displaystyle \phi }$ 和 ${\displaystyle u_{0}}$，${\displaystyle \phi }$ 是cutoff line和縱軸f-axis的夾角，而 ${\displaystyle u_{0}}$ 則是cutoff line 距離原點的距離。

以下示範如何使用分數傅立葉轉換和Cutoff line來將噪音濾除:

步驟(1) 首先決定cutoff line和縱軸f-axis的夾角 ${\displaystyle \phi }$

步驟(2) 利用分數傅立葉轉換對時頻分布旋轉 ${\displaystyle \phi }$，使 cutoff line 垂直橫軸 t-axis。

步驟(3) 算出 ${\displaystyle u_{0}}$後，再利用低通遮罩(Low pass Mask)將噪音濾掉。

步驟(4) 最後再做一次分數傅立葉轉換 ${\displaystyle -\phi }$，將時頻分布旋轉回原來的位置。

令接收到的信號為 ${\displaystyle x_{i}(t)}$，最後得到的信號為 ${\displaystyle x_{o}(t)}$，可將以上步驟用數學式子表示如下:

${\displaystyle x_{o}(t)=X_{-\phi }[{X_{\phi }(x_{i}(t))H(u)}]}$

${\displaystyle H(u)={\begin{cases}1,&{\mbox{if}}u<u_{0}{\mbox{ }}\\0,&{\mbox{if}}u>u_{0}{\mbox{ }}\end{cases}}}$

例子二:

假設發射一信號s(t)，中間受到雜訊干擾，最後收到的訊號為f(t)=s(t)+noise

(a) 發射訊號的時域圖

(b) 接收訊號的時域圖

(c) 發射訊號的韋格納分布

(d) 接收訊號的韋格納分布，有由此可見cross-term已經大大的影響時頻圖的可見姓，加上雜訊後的韋格納分布更是無法清楚地將訊號分離開來

(e) 發射訊號的加伯轉換

(f) 接收訊號的加伯轉換

(g) 接收訊號的加伯-維格納轉換

(h) 濾波器的設計，這邊總共有四條cutoff lines，其中有兩條平行，所以總共需要做三次不同的分數傅立葉轉換，再藉由cutoff lines來去除雜訊

(i) 濾波器的設計，這邊總共有四條cutoff lines，其中有兩條平行，所以總共需要做三次不同的分數傅立葉轉換，再藉由cutoff lines來去除雜訊

(j) 對(i)做分數傅立葉轉換

(k) 利用高通濾波器濾波，把兩條cutoff lines設置在低頻

(l) 經過(k)濾波器以後

(m) 透過同上的手法再做兩次低通濾波器，把旁邊兩條線給去除後可得到的還原訊號

(n) 發射訊號(藍色)和還原訊號(綠色)的比較，兩者的MSE僅有0.1128%

由以上可知，透過分數傅立葉旋轉時頻圖的技巧來設計濾波器，我們可以精準地還原訊號

例子三:

一樣假設接收訊號受到了雜訊干擾

(a) 發射訊號

(b) 接收訊號

(c) 接收訊號的韋格納分

(d) 接收訊號的加伯轉換

(e) 接收訊號的加伯-維格納轉換，在這邊的濾波器需要五條cutoff lines(藍線)，但有兩條是垂直時間軸，可以直接在時間軸上去除，剩下的三條則需要利用分數傅立葉轉換來去除。

(f) 還原訊號，MSE僅0.3013%

傅立葉轉換

優點: 運算複雜度較低，有快速傅立葉轉換的演算法。

缺點: 僅有一個維度，頻域，來分析；雜訊若和訊號重疊，則難以分離。

分數傅立葉轉換

優點: 運用旋轉的技巧在時頻圖上去除雜訊，多了一個維度（時域）來分析；除非雜訊和訊號同時在頻域和時域上重疊，否則將可以分離兩訊號。

缺點: 運算複雜度較高。

其他的時間-頻率變換：

• 短時傅立葉變換
• 小波變換
• chirplet變換

• DiscreteTFDs -- software for computing the fractional Fourier transform and time-frequency distributions （页面存档备份，存于互联网档案馆）
• Class notes of Time frequency analysis and wavelet transform -- from Prof. Jian-Jiun Ding's course website （页面存档备份，存于互联网档案馆）

• N. Wiener, "Hermitian polynomials and Fourier analysis," Journal of Mathematics Physics MIT, 18, 70-73 (1929).
• V. Namias, "The fractional order Fourier transform and its application to quantum mechanics," J. Inst. Appl. Math. 25, 241–265 (1980).
• Luís B. Almeida, "The fractional Fourier transform and time-frequency representations," IEEE Trans. Sig. Processing 42 (11), 3084–3091 (1994).
• Soo-Chang Pei and Jian-Jiun Ding, "Relations between fractional operations and time-frequency distributions, and their applications," IEEE Trans. Sig. Processing 49 (8), 1638–1655 (2001).
• D. H. Bailey and P. N. Swarztrauber, "The fractional Fourier transform and applications," SIAM Review 33, 389-404 (1991). (Note that this article refers to the chirp-z transform variant, not the FRFT.)
• Haldun M. Ozaktas, Zeev Zalevsky and M. Alper Kutay. "The Fractional Fourier Transform with Applications in Optics and Signal Processing". John Wiley & Sons (2001). Series in Pure and Applied Optics.
• Jian-Jiun Ding, Time frequency analysis and wavelet transform class note, Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2013