同调 - 维基百科，自由的百科全书

数学上（特别是代数拓扑和抽象代数），同调 （homology，在希腊语中homos = 同）是一类将一个可换群或者模的序列和特定数学对象（例如拓扑空间或者群）联系起来的过程。背景知识请参看同调论。

对于一个特定的拓扑空间，同调群通常比同伦群要容易计算得多，因此通常来讲用同调来辅助空间分类要容易处理一些。

同调群的构造[编辑]

其过程如下：给定对象${\displaystyle X}$，首先定义链复形，它包含了${\displaystyle X}$的信息。一个链复形是一个由群同态联系起来的可换群或者模${\displaystyle A_{0},A_{1},A_{2},\dots }$的序列，群同态${\displaystyle d_{n}:A_{n}\rightarrow A_{n-1}}$满足任何两个相连的同态的复合为0: ${\displaystyle d_{n}\circ d_{n+1}=0}$对于所有${\displaystyle n}$成立。这意味着第${\displaystyle n+1}$个映射的像包含在第${\displaystyle n}$个映射的核中，我们定义${\displaystyle X}$的${\displaystyle n}$阶同调群为商群（商模）

${\displaystyle H_{n}(X)=\mathrm {ker} (d_{n})/\mathrm {im} (d_{n+1}).}$

链复形称为正合的，如果（${\displaystyle n+1}$）阶映射的像总是等于${\displaystyle n}$阶映射的核。因此${\displaystyle X}$的同调群是衡量${\displaystyle X}$所关联的链复形离正合有“多远”的障碍。

非正式的例子[编辑]

非正式地，拓扑空间X的同调是X的拓扑不变量的集合，用其同调群来表示

${\displaystyle H_{0}(X),H_{1}(X),H_{2}(X),\ldots }$

其中第${\displaystyle k}$个同调群${\displaystyle H_{k}(X)}$描绘了${\displaystyle X}$中的${\displaystyle k}$维圈 (cycle)，实现为${\displaystyle k+1}$维圆盘边界 (boundary) 的障碍。0维同调群刻画了两个零维圈，也即点，实现成一维圆盘，也即线段的边界的障碍，因此${\displaystyle H_{0}(X)}$刻画了${\displaystyle X}$中的道路连通分支。^[1]

一维球面 ${\displaystyle S^{1}}$是一个圆。它有一个连通分支和一个一维圈，但没有更高维圈。其对应的同调群由下式给出

${\displaystyle H_{k}(S^{1})\cong {\begin{cases}\mathbb {Z} &k=0,1\\0&k\neq 0,1\end{cases}}}$

其中${\displaystyle \mathbb {Z} }$表示整数加群，${\displaystyle 0}$表示平凡群。${\displaystyle H_{1}(S^{1})\cong \mathbb {Z} }$表示${\displaystyle S^{1}}$的一阶同调群为由一个元素生成的有限生成阿贝尔群，其唯一的生成元表示圆中包含的一维圈。^[2]

二维球面${\displaystyle S^{2}}$有一个连通分支，零个一维圈，一个二维圈（即球面），无更高维的圈，其对应的同调群为^[2]

${\displaystyle H_{k}(S^{2})\cong {\begin{cases}\mathbb {Z} &k=0,2\\0&k\neq 0,2\end{cases}}}$

一般地，对${\displaystyle n}$维球面${\displaystyle S^{n}}$，其同调群为

${\displaystyle H_{k}(S^{n})\cong {\begin{cases}\mathbb {Z} &k=0,n\\0&k\neq 0,n\end{cases}}}$

二维实心球${\displaystyle B^{2}}$有一个道路连通分支，但与圆不同的是，${\displaystyle B^{2}}$没有一维或更高维的圈，其对应的同调群除了零阶同调群${\displaystyle H_{0}(B^{2})\cong \mathbb {Z} }$以外，其余阶的同调群均为平凡群。

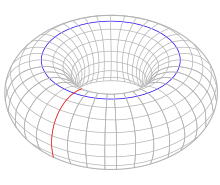环面被定义为两个圆${\displaystyle T^{2}=S^{1}\times S^{1}}$的笛卡尔积。环面有一个道路连通分支，两个独立的一维圈（在图中以红圈和蓝圈分别标出），以及一个二维圈（环面的内部）。其对应的同调群为^[3]

${\displaystyle H_{k}(T^{2})\cong {\begin{cases}\mathbb {Z} &k=0,2\\\mathbb {Z} \times \mathbb {Z} &k=1\\0&k\geq 3\end{cases}}}$

两个独立的一维圈组成了一组有限生成阿贝尔群的独立生成元，表示为笛卡尔积群${\displaystyle \mathbb {Z} \times \mathbb {Z} }$.

例子[编辑]

引入同调的概念可以用单纯复形${\displaystyle X}$的单纯同调：设${\displaystyle C_{n}}$为${\displaystyle X}$中的${\displaystyle n}$维可定向单纯形生成的自由交换群或者模，映射${\displaystyle \partial _{n}:C_{n}\rightarrow C_{n+1}}$映射称为边缘映射 (boundary map)，它将${\displaystyle n}$维单纯形

${\displaystyle \sigma :\Delta ^{n}\rightarrow X}$

映射为如下交错和

${\displaystyle \sum _{i=0}^{n}(-1)^{i}\sigma |_{[e_{0},\ldots ,e_{i-1},e_{i+1},\ldots ,e_{n}]}.}$

，其中${\displaystyle \sigma |_{[e_{0},\cdots ,e_{i-1},e_{i+1},\cdots ,e_{n}]}}$表示${\displaystyle \sigma }$限制在${\displaystyle e_{0},\cdots ,e_{i-1},e_{i+1},\cdots ,e_{n}}$对应的面 (face)上。如果我们将模取在一个域上，则${\displaystyle X}$的${\displaystyle n}$阶同调的维数就是${\displaystyle X}$中${\displaystyle n}$维圈的个数。

仿照单纯同调群，可以定义任何拓扑空间${\displaystyle X}$的奇异同调群。我们定义${\displaystyle X}$的上同调的链复形中的空间为${\displaystyle A_{n}}$为自由交换群（或者自由模），其生成元为所有从${\displaystyle n}$为单纯形到${\displaystyle X}$的连续函数。同态${\displaystyle d_{n}}$从单纯形的边缘映射得到。

同调代数中，同调用于定义导出函子，例如，Tor函子。这里，我们可以从某个可加协变函子${\displaystyle F}$和某个模${\displaystyle X}$开始。${\displaystyle X}$的链复形定义如下：首先找到一个自由模${\displaystyle F_{1}}$和一个满同态${\displaystyle p_{1}:F_{1}\rightarrow X}$。然后找到一个自由模${\displaystyle F_{2}}$和一个满同态${\displaystyle p_{2}:F_{2}\rightarrow \mathrm {ker} (p_{1})}$。以该方式继续，得到一个自由模${\displaystyle F_{n}}$和同态${\displaystyle p_{n}}$的序列。将函子${\displaystyle F}$应用于这个序列，得到一个链复形；这个复形的同调${\displaystyle H_{n}}$仅依赖于${\displaystyle F}$和${\displaystyle X}$，并且按定义就是${\displaystyle F}$作用于${\displaystyle X}$的n阶导出函子。

同调函子[编辑]

链复形构成一个范畴：从链复形${\displaystyle (d_{n}:A_{n}\rightarrow A_{n-1})}$到链复形${\displaystyle (e_{n}:B_{n}\rightarrow B_{n-1})}$的态射是一个同态的序列${\displaystyle (f_{n}:A_{n}\rightarrow B_{n})}$，满足${\displaystyle f_{n-1}\circ d_{n}=e_{n-1}\circ f_{n}}$对于所有${\displaystyle n}$成立。${\displaystyle n}$阶同调 ${\displaystyle H_{n}}$可以视为一个从链复形的范畴到可换群（或者模）的范畴的协变函子。

若链复形以协变的方式依赖于对象${\displaystyle X}$（也就是任何态射${\displaystyle X\rightarrow Y}$诱导出一个从${\displaystyle X}$的链复形到${\displaystyle Y}$的链复形的态射），则${\displaystyle H_{n}}$是从${\displaystyle X}$所属的范畴到可换群（或模）的范畴的函子。

同调和上同调的唯一区别是上同调中的链复形以逆变方式依赖于${\displaystyle X}$，因此其同调群（在这个情况下称为上同调群并记为${\displaystyle H^{n}}$）构成从${\displaystyle X}$所属的范畴到可换群或者模的范畴的逆变函子。

性质[编辑]

若${\displaystyle (d_{n}:A_{n}\rightarrow A_{n-1})}$是链复形，满足出有限个${\displaystyle A_{n}}$外所有项都是零，而非零的都是有限生成可换群（或者有限维向量空间），则可以定义欧拉示性数

${\displaystyle \chi =\sum (-1)^{n}\,\mathrm {rank} (A_{n})}$

（可换群采用阶而向量空间的情况采用哈默尔维数）。事实上在同调水平上也可以计算欧拉示性数:

${\displaystyle \chi =\sum (-1)^{n}\,\mathrm {rank} (H_{n})}$

特别地，在代数拓扑中，欧拉示性数${\displaystyle \chi }$是拓扑空间的重要不变量。

此外，每个链复形的短正合序列

${\displaystyle 0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0}$

诱导一个同调群的长正合序列

${\displaystyle \cdots \rightarrow H_{n}(A)\rightarrow H_{n}(B)\rightarrow H_{n}(C)\rightarrow H_{n-1}(A)\rightarrow H_{n-1}(B)\rightarrow H_{n-1}(C)\rightarrow H_{n-2}(A)\rightarrow \cdots \,}$

这个长正合序列中的所有映射由链复形间的映射导出，除了映射${\displaystyle H_{n}(C)\rightarrow H_{n-1}(A)}$之外。后者称为连接同态，由蛇引理给出。

参看[编辑]

• 奇异同调
• 上同调
• 同调论
• 同调代数

參考文獻[编辑]

• Hatcher, A. Algebraic Topology. Cambridge University Press. 2002 [2021-11-18]. ISBN 0-521-79540-0. （原始内容存档于2018-05-15）.  有仔細討論單複形、流形的同調論、奇異同調等。
• Gowers, Timothy; Barrow-Green, June; Leader, Imre (编). The Princeton Companion to Mathematics. Princeton University Press. 2010. ISBN 9781400830398. 
• Spanier, Edwin H. Algebraic Topology. Springer. 1966: 155. ISBN 0-387-90646-0.