钟形孤立子 正弦-戈尔登方程 是十九世纪发现的一种偏微分方程:
φ t t − φ x x = sin φ {\displaystyle \varphi _{tt}-\varphi _{xx}=\sin \varphi }
來自下面的拉量 :
L = 1 2 ( φ t 2 − φ x 2 ) + cos φ {\displaystyle {\mathcal {L}}={\frac {1}{2}}(\varphi _{t}^{2}-\varphi _{x}^{2})+\cos \varphi }
由于正弦-戈尔登方程有多种孤立子 解而倍受瞩目。
名字是物理家熟悉的克莱因-戈尔登方程 (Klein-Gordon)的雙關語。[ 1]
利用分离变数法 可得正弦-戈尔登方程的多种孤立子解。[ 2]
p 1 := − 4 ∗ a r c t a n ( ( 1 / 2 ) ∗ ( 1.5 ∗ e x p ( − 4 ∗ s q r t ( 2 ) ) − e x p ( 2 ∗ x ∗ s q r t ( 2 ) ) ) ∗ e x p ( t − 2 − x ∗ s q r t ( 2 ) + 2 ∗ s q r t ( 2 ) ) ∗ s q r t ( 2 ) / ( 1.5 ∗ e x p ( − 4 ) + e x p ( 2 ∗ t ) ) ) {\displaystyle p1:=-4*arctan((1/2)*(1.5*exp(-4*sqrt(2))-exp(2*x*sqrt(2)))*exp(t-2-x*sqrt(2)+2*sqrt(2))*sqrt(2)/(1.5*exp(-4)+exp(2*t)))}
p 2 := − 4 ∗ a r c t a n ( ( 1 / 2 ) ∗ ( 1.5 ∗ e x p ( 2 ∗ x ∗ s q r t ( 2 ) ) − e x p ( − 4 ∗ s q r t ( 2 ) ) ) ∗ e x p ( t − 2 − x ∗ s q r t ( 2 ) + 2 ∗ s q r t ( 2 ) ) ∗ s q r t ( 2 ) / ( 1.5 ∗ e x p ( 2 ∗ t ) + e x p ( − 4 ) ) ) {\displaystyle p2:=-4*arctan((1/2)*(1.5*exp(2*x*sqrt(2))-exp(-4*sqrt(2)))*exp(t-2-x*sqrt(2)+2*sqrt(2))*sqrt(2)/(1.5*exp(2*t)+exp(-4)))}
Sine-Gordon kink soliton plot1 Sine-Gordon kink soliton plot2
正弦-戈尔登方程有如下孤立子解:
φ soliton ( x , t ) := 4 arctan e m γ ( x − v t ) + δ {\displaystyle \varphi _{\text{soliton}}(x,t):=4\arctan e^{m\gamma (x-vt)+\delta }\,} 其中
γ 2 = 1 1 − v 2 . {\displaystyle \gamma ^{2}={\frac {1}{1-v^{2}}}.} 顺时针孤立子 反时针孤立子
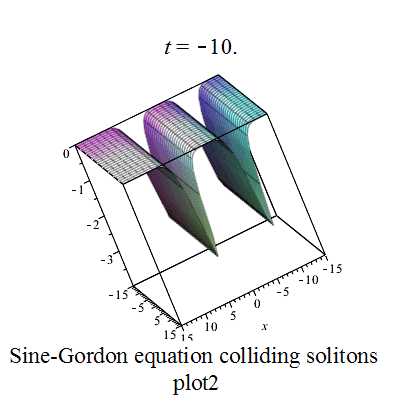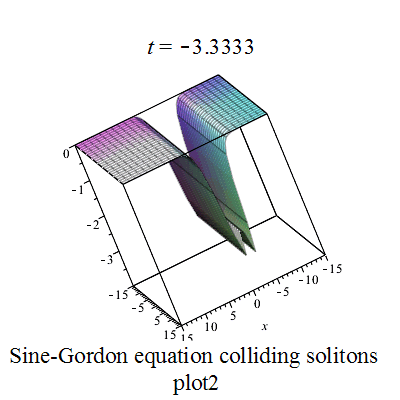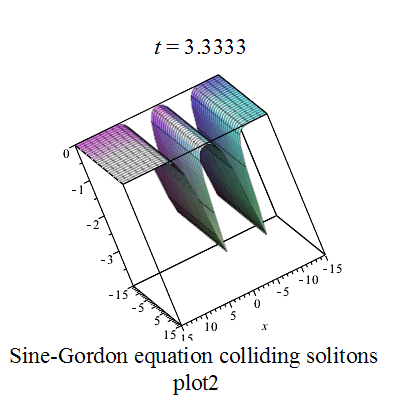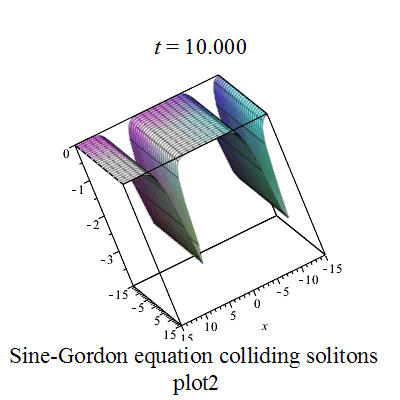
p x 1 := ( 8 ∗ ( 1.5 ∗ e x p ( − 4 ) + e x p ( 2 ∗ t ) ) ) ∗ e x p ( t − 2 − x ∗ s q r t ( 2 ) + 2 ∗ s q r t ( 2 ) ) ∗ ( e x p ( 2 ∗ x ∗ s q r t ( 2 ) ) + 1.5 ∗ e x p ( − 4 ∗ s q r t ( 2 ) ) ) / ( 4.50 ∗ e x p ( − 8 ) + 2 ∗ e x p ( 4 ∗ t ) + 2.25 ∗ e x p ( 2 ∗ t − 4 − 2 ∗ x ∗ s q r t ( 2 ) − 4 ∗ s q r t ( 2 ) ) + 3.0 ∗ e x p ( 2 ∗ t − 4 ) + e x p ( 2 ∗ t − 4 + 2 ∗ x ∗ s q r t ( 2 ) + 4 ∗ s q r t ( 2 ) ) ) {\displaystyle px1:=(8*(1.5*exp(-4)+exp(2*t)))*exp(t-2-x*sqrt(2)+2*sqrt(2))*(exp(2*x*sqrt(2))+1.5*exp(-4*sqrt(2)))/(4.50*exp(-8)+2*exp(4*t)+2.25*exp(2*t-4-2*x*sqrt(2)-4*sqrt(2))+3.0*exp(2*t-4)+exp(2*t-4+2*x*sqrt(2)+4*sqrt(2)))}
p x 2 := − ( 8 ∗ ( 1.5 ∗ e x p ( 2 ∗ t ) + e x p ( − 4 ) ) ) ∗ e x p ( t − 2 − x ∗ s q r t ( 2 ) + 2 ∗ s q r t ( 2 ) ) ∗ ( 1.5 ∗ e x p ( 2 ∗ x ∗ s q r t ( 2 ) ) + e x p ( − 4 ∗ s q r t ( 2 ) ) ) / ( 4.50 ∗ e x p ( 4 ∗ t ) + 2 ∗ e x p ( − 8 ) + 2.25 ∗ e x p ( 2 ∗ t − 4 + 2 ∗ x ∗ s q r t ( 2 ) + 4 ∗ s q r t ( 2 ) ) + 3.0 ∗ e x p ( 2 ∗ t − 4 ) + e x p ( 2 ∗ t − 4 − 2 ∗ x ∗ s q r t ( 2 ) − 4 ∗ s q r t ( 2 ) ) ) {\displaystyle px2:=-(8*(1.5*exp(2*t)+exp(-4)))*exp(t-2-x*sqrt(2)+2*sqrt(2))*(1.5*exp(2*x*sqrt(2))+exp(-4*sqrt(2)))/(4.50*exp(4*t)+2*exp(-8)+2.25*exp(2*t-4+2*x*sqrt(2)+4*sqrt(2))+3.0*exp(2*t-4)+exp(2*t-4-2*x*sqrt(2)-4*sqrt(2)))}
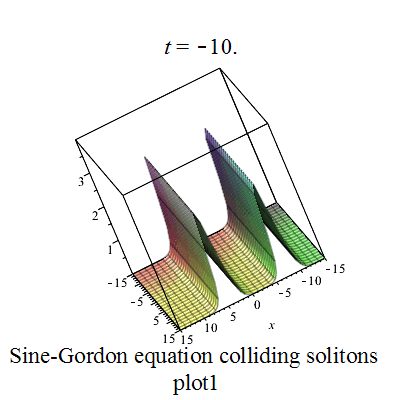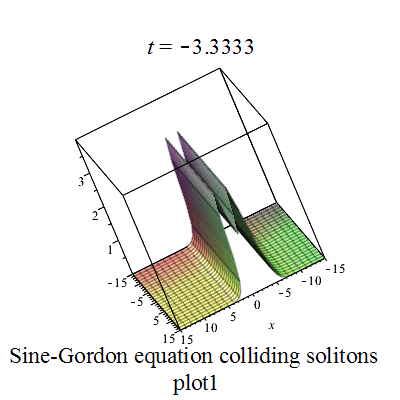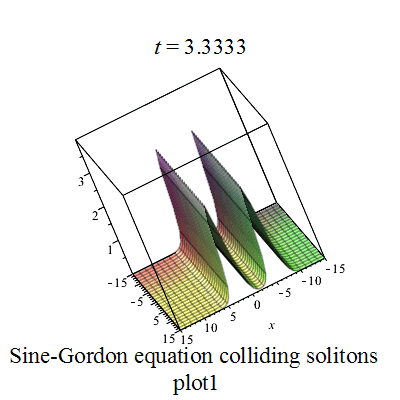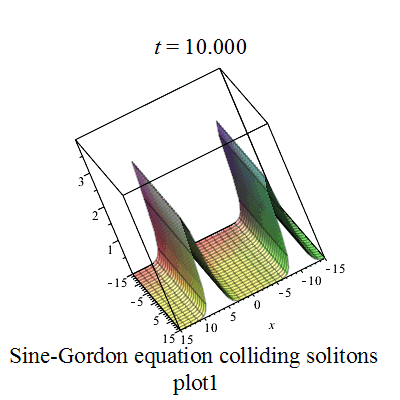
Sine-Gordon colliding soltons plot1 Sine-Gordon colliding soltons plot2
Sine-Gordon bright & dark solitons plot1 & dark solitons plot2
扭型与反扭型碰撞 扭型-扭型碰撞
扭型行波呼吸子与驻波呼吸子碰撞 反扭型行波呼吸子与驻波波呼吸子碰撞
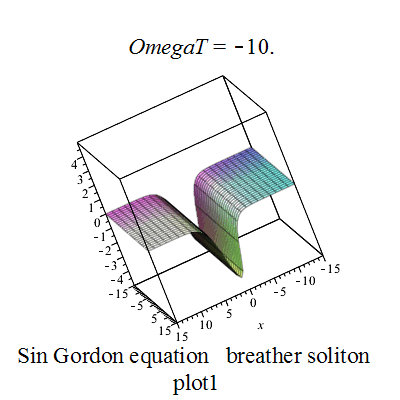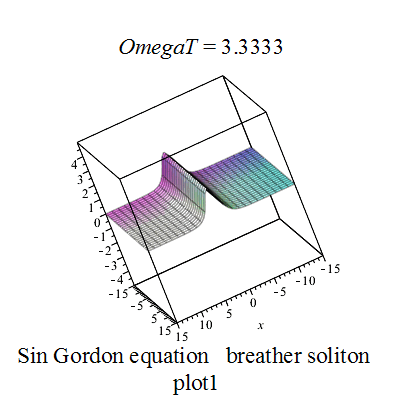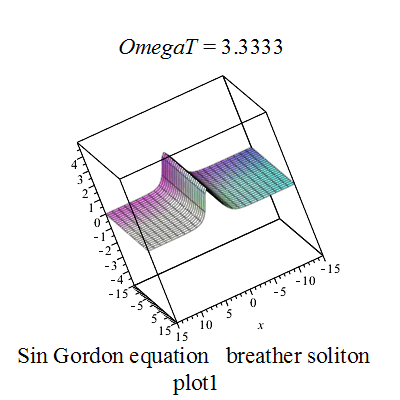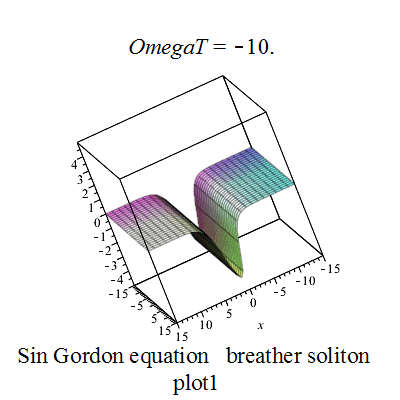
正弦-戈尔登方程的呼吸子解 u = 4 arctan ( 1 − ω 2 cos ( ω t ) ω cosh ( 1 − ω 2 x ) ) , {\displaystyle u=4\arctan \left({\frac {{\sqrt {1-\omega ^{2}}}\;\cos(\omega t)}{\omega \;\cosh({\sqrt {1-\omega ^{2}}}\;x)}}\right),} p z 1 := 4 ∗ a r c t a n ( ( 28.460498941515413988 ∗ ( e x p ( 1.8973665961010275992 ∗ x ) + s q r t ( e x p ( 3.7947331922020551984 ∗ x ) ) ) ) ∗ s i n ( O m e g a T ) ∗ c s g n ( 1 / c o s ( O m e g a T ) ) ∗ e x p ( − .94868329805051379960 ∗ x ) / ( 18. + 5. ∗ e x p ( 1.8973665961010275992 ∗ x ) ) ) {\displaystyle pz1:=4*arctan((28.460498941515413988*(exp(1.8973665961010275992*x)+sqrt(exp(3.7947331922020551984*x))))*sin(OmegaT)*csgn(1/cos(OmegaT))*exp(-.94868329805051379960*x)/(18.+5.*exp(1.8973665961010275992*x)))}
p z 2 := 4 ∗ a r c t a n ( ( 28.460498941515413988 ∗ ( e x p ( 1.8973665961010275992 ∗ x ) + s q r t ( e x p ( 3.7947331922020551984 ∗ x ) ) ) ) ∗ s i n ( O m e g a T ) ∗ c s g n ( 1 / c o s ( O m e g a T ) ) ∗ e x p ( − .94868329805051379960 ∗ x ) / ( 18. + 5. ∗ e x p ( 1.8973665961010275992 ∗ x ) ) ) {\displaystyle pz2:=4*arctan((28.460498941515413988*(exp(1.8973665961010275992*x)+sqrt(exp(3.7947331922020551984*x))))*sin(OmegaT)*csgn(1/cos(OmegaT))*exp(-.94868329805051379960*x)/(18.+5.*exp(1.8973665961010275992*x)))}
Sine-Gordon breather plot1 Sine-Gordon breather plot2
三维欧几里德空间的负常曲率曲面 根據陳省身 的研究,正弦-戈尔登方程有一个几何解释:三维欧几里德空间 的负常曲率 曲面(偽球面 )。[ 3]
正弦-戈尔登方程是:[ 4]
φ t t − φ x x = sinh φ {\displaystyle \varphi _{tt}-\varphi _{xx}=\sinh \varphi }
跟戶田場論 [ 5]
正弦-戈尔登是Thirring模特 S對偶 。
半經典量子化:[ 6]
^ Rajaraman, R. Solitons and instantons : an introduction to solitons and instantons in quantum field theory. Amsterdam https://www.worldcat.org/oclc/17480018 . (1987 [printing]). ISBN 0-444-87047-4OCLC 17480018 ^ Inna Shingareva Carlos Lizarraga Celaya, Solving Nonlinear Partial Differential Equations with Maple and Mathematica, p86-94,Springer ^ 陈省身 Geometrical interpretation of the sinh-Gordon equation。annals Polonici Mathematici XXXIX 1981^ Poli︠a︡nin, A. D. (Andreĭ Dmitrievich). Handbook of nonlinear partial differential equations. 2nd ed. Boca Raton, FL: CRC Press https://www.worldcat.org/oclc/751520047 . 2012. ISBN 978-1-4200-8723-9OCLC 751520047 ^ Xie, Yuanxi; Tang, Jiashi. A unified method for solving sinh-Gordon-type equations . Il Nuovo Cimento B. 2006-05-10, 121 (2): 115–120. ISSN 0369-3554 doi:10.1393/ncb/i2005-10164-6 ^ Faddeev, L.D.; Korepin, V.E. Quantum theory of solitons . Physics Reports. 1978-06, 42 (1): 1–87 [2020-02-03 ] . doi:10.1016/0370-1573(78)90058-3 存档 于2021-03-08) (英语) . Bour E (1862). "Théorie de la déformation des surfaces" (页面存档备份 ,存于互联网档案馆 ). J. Ecole Imperiale Polytechnique. 19: 1–48. Rajaraman, R. (1989). Solitons and Instantons: An Introduction to Solitons and Instantons in Quantum Field Theory. North-Holland Personal Library. 15. North-Holland. pp. 34–45. ISBN 978-0-444-87047-6 . Polyanin, Andrei D.; Valentin F. Zaitsev (2004). Handbook of Nonlinear Partial Differential Equations. Chapman & Hall/CRC Press. pp. 470–492. ISBN 978-1-58488-355-5 . Dodd, Roger K.; J. C. Eilbeck, J. D. Gibbon, H. C. Morris (1982). Solitons and Nonlinear Wave Equations. London: Academic Press. ISBN 978-0-12-219122-0 . Georgiev DD, Papaioanou SN, Glazebrook JF (2004). "Neuronic system inside neurons: molecular biology and biophysics of neuronal microtubules". Biomedical Reviews 15: 67–75. Georgiev DD, Papaioanou SN, Glazebrook JF (2007). "Solitonic effects of the local electromagnetic field on neuronal microtubules". Neuroquantology 5 (3): 276–291.
基本对象 背景理論 微扰弦理论 非微扰结果 现象学 数学方法 几何 规范场论 超对称 理论家



















 French
French Deutsch
Deutsch












