| 线性代数 |
 |
| 向量 · 向量空间 · 基底 · 行列式 · 矩阵 |
| |
| |
| 「横(row)」的各地常用名稱 |
|---|
| 中国大陸 | 行 |
|---|
| 臺灣 | 列[1] |
|---|
行列式(英語:Determinant),记作 或
或 ,是一个在方块矩阵上计算得到的标量。行列式可以看作是有向面积或体积的概念在一般的欧几里得空间中的推广。或者说,在欧几里得空间中,行列式描述的是一个线性变换对“体积”所造成的影响。无论是在线性代数、多项式理论,还是在微积分学中(比如说换元积分法中),行列式作为基本的数学工具,都有着重要的应用。
,是一个在方块矩阵上计算得到的标量。行列式可以看作是有向面积或体积的概念在一般的欧几里得空间中的推广。或者说,在欧几里得空间中,行列式描述的是一个线性变换对“体积”所造成的影响。无论是在线性代数、多项式理论,还是在微积分学中(比如说换元积分法中),行列式作为基本的数学工具,都有着重要的应用。
行列式概念最早出现在解线性方程组的过程中。十七世纪晚期,关孝和与莱布尼茨的著作中已经使用行列式来确定线性方程组解的个数以及形式。十八世纪开始,行列式开始作为独立的数学概念被研究。十九世纪以后,行列式理论进一步得到发展和完善。矩阵概念的引入使得更多有关行列式的性质被发现,行列式在许多领域都逐渐显现出重要的意义和作用,其定义也被推广到诸如线性自同态和向量组等结构上。
行列式的特性可以被概括为一个交替多线性形式,这个本质使得行列式在欧几里德空间中可以成为描述“体积”的函数[2]。
矩陣 的行列式記作
的行列式記作 。行列式經常使用竖直線記法(例如:克萊姆法則和子式)。例如,对于一個矩陣:
。行列式經常使用竖直線記法(例如:克萊姆法則和子式)。例如,对于一個矩陣:

 也记作
也记作 ,或以細長的垂直線取代矩陣的方括號,明確的寫为[3][4]:
,或以細長的垂直線取代矩陣的方括號,明確的寫为[3][4]:

当这个记法用于絕對值时,其作用对象为数,矩陣的絕對值是无定義的。矩陣範數通常以雙垂直線來表示(如: ),且可以使用下標。故不会与二者造成混淆。
),且可以使用下標。故不会与二者造成混淆。
一个 阶方块矩阵
阶方块矩阵 的行列式可直观地定义如下:
的行列式可直观地定义如下:

其中, 是集合
是集合 上置换的全体,即集合
上置换的全体,即集合 到自身上的一一映射(双射)的全体;
到自身上的一一映射(双射)的全体;
 表示对
表示对 全部元素的求和,即对于每个
全部元素的求和,即对于每个 ,
, 在加法算式中出现一次;对每一个满足
在加法算式中出现一次;对每一个满足 的数对
的数对 ,
, 是矩阵
是矩阵 的第
的第 行第
行第 列的元素。
列的元素。
 表示置换
表示置换 的符号差,具体地说,满足
的符号差,具体地说,满足 但
但 的有序数对
的有序数对 称为
称为 的一个逆序。
的一个逆序。
如果 的逆序共有偶数个,则
的逆序共有偶数个,则 ,如果共有奇数个,则
,如果共有奇数个,则 。
。
举例来说,对于3元置换 (即是说
(即是说 ,
, ,
, )而言,由于1在2后,1在3后,所以共有2个逆序(偶数个),因此
)而言,由于1在2后,1在3后,所以共有2个逆序(偶数个),因此 ,从而3阶行列式中项
,从而3阶行列式中项 的符号是正的。但对于三元置换
的符号是正的。但对于三元置换 (即是说
(即是说 ,
, ,
, )而言,可以数出共有3个逆序(奇数个),因此
)而言,可以数出共有3个逆序(奇数个),因此 ,从而3阶行列式中项
,从而3阶行列式中项 的符号是负号[5][6]。
的符号是负号[5][6]。
注意到对于任意正整数 ,
, 共拥有n!个元素,因此上式中共有
共拥有n!个元素,因此上式中共有 个求和项,即这是一个有限多次的求和。
个求和项,即这是一个有限多次的求和。
对于简单的2阶和3阶的矩阵,行列式的表达式相对简单,而且恰好是每条主对角线(左上至右下)元素乘积之和减去每条副对角线(右上至左下)元素乘积之和(见图中红线和蓝线)。
- 2阶矩阵的行列式:
 [7]
[7]
- 3阶矩阵的行列式:
 [8]
[8]
 三阶矩阵的行列式为每条红线上的元素的乘积之和,减去蓝线上元素乘积之和。
三阶矩阵的行列式为每条红线上的元素的乘积之和,减去蓝线上元素乘积之和。 但对于阶数 的方阵
的方阵 ,这样的主对角线和副对角线分别只有
,这样的主对角线和副对角线分别只有 条,由于
条,由于 的主、副对角线总条数
的主、副对角线总条数 的元素个数 因此,行列式的相加项中除了这样的对角线乘积之外,还有其他更多的项。例如4阶行列式中,项
的元素个数 因此,行列式的相加项中除了这样的对角线乘积之外,还有其他更多的项。例如4阶行列式中,项 就不是任何对角线的元素乘积。不过,和2、3阶行列式情况相同的是,n阶行列式中的每一项仍然是从矩阵中选取n个元素相乘得到,且保证在每行和每列中都恰好只选取一个元素,而整个行列式恰好将所有这样的选取方法遍历一次。
就不是任何对角线的元素乘积。不过,和2、3阶行列式情况相同的是,n阶行列式中的每一项仍然是从矩阵中选取n个元素相乘得到,且保证在每行和每列中都恰好只选取一个元素,而整个行列式恰好将所有这样的选取方法遍历一次。
另外, 矩阵的每一行或每一列也可以看成是一个
矩阵的每一行或每一列也可以看成是一个 元向量,这时矩阵的行列式也被称为这
元向量,这时矩阵的行列式也被称为这 个
个 元向量组成的向量组的行列式[9]。
元向量组成的向量组的行列式[9]。
行列式的一个自然的源起是n维平行体的体积。行列式的定义和n维平行体的体积有着本质上的关联[10]。
 行列式是向量形成的平行四边形的面积
行列式是向量形成的平行四边形的面积 在一个二维平面上,两个向量 和
和 的行列式是:
的行列式是:
 [7]
[7]
比如说,两个向量 和
和 的行列式是:
的行列式是:

经计算可知,当系数是实数时,行列式表示的是向量 和
和 形成的平行四边形的有向面积,并有如下性质:
形成的平行四边形的有向面积,并有如下性质:
- 行列式为零当且仅当两个向量共线(线性相关),这时平行四边形退化成一条直线[9]。
- 如果以逆时针方向为正向的话,有向面积的意义是:平行四边形面积为正当且仅当以原点为不动点将
 逆时针“转到”
逆时针“转到” 处时,扫过的地方在平行四边形裡,否则的话面积就是负的。如右图中,
处时,扫过的地方在平行四边形裡,否则的话面积就是负的。如右图中, 和
和 所构成的平行四边形的面积就是正的[11]。
所构成的平行四边形的面积就是正的[11]。 - 行列式是一个双线性映射。也就是说,
 ,
,
- 并且
 [9]。
[9]。
 行列式
行列式 其几何意义是:以同一个向量 作为一条边的两个平行四边形的面积之和,等于它们各自另一边的向量
作为一条边的两个平行四边形的面积之和,等于它们各自另一边的向量 和
和 加起来后的向量:
加起来后的向量: 和
和 所构成的平行四边形的面积,如左图中所示。
所构成的平行四边形的面积,如左图中所示。
在三维的有向空间中,三个三维向量的行列式是:
 。[8]
。[8]
比如说,三个向量 、
、 和
和 的行列式是:
的行列式是:

当系数是实数时,行列式表示 、
、 和
和 三个向量形成的平行六面体的有向体积,也叫做这三个向量的混合积。同样的,可以观察到如下性质[12]:
三个向量形成的平行六面体的有向体积,也叫做这三个向量的混合积。同样的,可以观察到如下性质[12]:
- 行列式为零当且仅当三个向量共线或者共面(三者线性相关),这时平行六面体退化为平面图形,体积为零[10]。
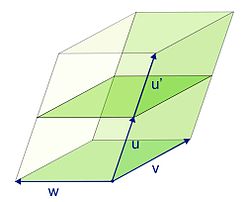 两个相邻平行六面体的体积之和
两个相邻平行六面体的体积之和 - 三维空间中有向体积的定义要比二维空间中复杂,一般是根据右手定则来约定。比如右图中(
 )所形成的平行六面体的体积是正的,而(
)所形成的平行六面体的体积是正的,而( )所形成的平行六面体的体积是负的。这个定义和行列式的计算并不矛盾,因为行列式中向量的坐标都是在取好坐标系后才决定的,而坐标系的三个方向一般也是按照右手规则来设定的。如果计算开始时坐标系的定向反过来的话,有向体积的定义也要跟着反过来,这样行列式才能代表有向体积[10][13]。
)所形成的平行六面体的体积是负的。这个定义和行列式的计算并不矛盾,因为行列式中向量的坐标都是在取好坐标系后才决定的,而坐标系的三个方向一般也是按照右手规则来设定的。如果计算开始时坐标系的定向反过来的话,有向体积的定义也要跟着反过来,这样行列式才能代表有向体积[10][13]。 - 这时行列式是一个“三线性映射”,也就是说,对第一个向量有
 ,对第二、第三个向量也是如此。其几何意义和二维时基本相同,是指当生成两个平行六面体的每组三个向量中如果有两个是重合的,比如分别是:(
,对第二、第三个向量也是如此。其几何意义和二维时基本相同,是指当生成两个平行六面体的每组三个向量中如果有两个是重合的,比如分别是:( )和(
)和( ),那么它们的体积之总和等于将
),那么它们的体积之总和等于将 和
和 加起来后的向量
加起来后的向量 和
和 ,
,  所形成的平行六面体的体积,如右图所示[10]。
所形成的平行六面体的体积,如右图所示[10]。
在以上的行列式中,我们不加选择地将向量在所谓的正交基(即直角坐标系)下分解,实际上在不同的基底之下,行列式的值并不相同。这并不是说平行六面体的体积不唯一。恰恰相反,这说明体积的概念依赖于衡量空间的尺度,也就是基底的取法。用基底的变换可以看作线性映射对基底的作用,而不同基底下的行列式代表了基变换对“体积”的影响。可以证明,对于所有同定向的标准正交基,向量组的行列式的值在绝对值意义上是一样的[14]。也就是说,如果我们选择的基底都是“单位长度”,并且两两正交,那么在这样的基之下,平行六面体的体积的绝对值是唯一的[15]。
 经线性映射后的正方体
经线性映射后的正方体 设E是一个一般的n维的有向欧几里得空间。一个线性变换把一个向量线性地变为另一个向量。比如说,在三维空间中,向量( )被映射到向量(
)被映射到向量( ):
):

其中 、
、 、
、 是系数。如右图,正方体(可以看作原来的一组基形成的)经线性变换后可以变成一个普通的平行六面体,或变成一个平行四边形(没有体积)。这两种情况表示了两种不同的线性变换,行列式可以将其很好地分辨出来(为零或不为零)。
是系数。如右图,正方体(可以看作原来的一组基形成的)经线性变换后可以变成一个普通的平行六面体,或变成一个平行四边形(没有体积)。这两种情况表示了两种不同的线性变换,行列式可以将其很好地分辨出来(为零或不为零)。
更详细地说,行列式表示的是线性变换前后平行六面体的体积的变化系数。如果设左边的正方体体积是一,那么中间的平行六面体的(有向)体积就是线性变换的行列式的值,右边的平行四边形体积为零,因为线性变换的行列式为零。这里我们混淆了线性变换的行列式和向量组的行列式,但两者是一样的,因为我们在对一组基作变换[16]。

以上二维和三维行列式的例子中,行列式被解释为向量形成的图形的面积或体积。面积或体积的定义是恒正的,而行列式是有正有负的,因此需要引入有向面积和有向体积的概念。负的面积或体积在物理学中可能难以理解,但在数学中,它们和有向角的概念类似,都是对空间镜面对称特性的一种刻画。如果行列式表示的是线性变换对体积的影响,那么行列式的正负就表示了空间的定向[17]。
如上图中,左边的黄色骰子(可以看成有单位的有向体积的物体)在经过了线性变换后变成中间绿色的平行六面体,这时行列式为正,两者是同定向的,可以通过旋转和拉伸从一个变成另一个。而骰子和右边的红色平行六面体之间也是通过线性变换得到的,但是无论怎样旋转和拉伸,都无法使一个变成另一个,一定要通过镜面反射才行。这时两者之间的线性变换的行列式是负的。可以看出,线性变换可以分为两类,一类对应着正的行列式,保持空间的定向不变,另一类对应负的行列式,颠倒空间的定向[17][18][19]。
由二维及三维的例子,可以看到一般的行列式应该具有怎样的性质。在 维欧几里得空间中,作为“平行多面体”的“体积”的概念的推广,行列式继承了“体积”函数的性质。首先,行列式需要是线性的,这可以由面积的性质类比得到。这裡的线性是对于每一个向量来说的,因为当一个向量变为原来的
维欧几里得空间中,作为“平行多面体”的“体积”的概念的推广,行列式继承了“体积”函数的性质。首先,行列式需要是线性的,这可以由面积的性质类比得到。这裡的线性是对于每一个向量来说的,因为当一个向量变为原来的 倍时,“平行多面体”的“体积”也变为原来的
倍时,“平行多面体”的“体积”也变为原来的 倍。其次,当一个向量在其它向量组成的“超平面”上时,
倍。其次,当一个向量在其它向量组成的“超平面”上时, 维“平行多面体”的“体积”是零(可以想像三维空间的例子)。也就是说,当向量线性相关时,行列式为零。在一般系数域上的线性空间中,行列式也正是由这样的特性所刻划的:
维“平行多面体”的“体积”是零(可以想像三维空间的例子)。也就是说,当向量线性相关时,行列式为零。在一般系数域上的线性空间中,行列式也正是由这样的特性所刻划的:
行列式是系数域为 的有限维线性空间
的有限维线性空间 上射到
上射到 的交替n-线性形式[20]。
的交替n-线性形式[20]。
具体来说,设 是一个系数在域
是一个系数在域 上的有限维线性空间,维数为
上的有限维线性空间,维数为 。一个
。一个 上的交替
上的交替 线性形式是指满足以下性质的函数
线性形式是指满足以下性质的函数 :
:
 重線性:
重線性:
- 交替性:
 或者说,当
或者说,当 的时候
的时候
所有E上的交替 线性形式的集合记作
线性形式的集合记作 。
。
定理:
 的维度是1。也就是说,设
的维度是1。也就是说,设 是
是 的一组基,那么,所有的交替
的一组基,那么,所有的交替 线性形式
线性形式 都可以写成
都可以写成

其中 是在基
是在基 下的展开[20][21]。
下的展开[20][21]。
证明:
对任一个 线性形式
线性形式 ,考虑将
,考虑将 依照多线性性质展开,
依照多线性性质展开,

这时,由交替性, 当且仅当
当且仅当 是
是 的一个排列,所以有
的一个排列,所以有

这裡, 。
。
设 是
是 的一组基,根据上面的定理和线性形式的性质,可以定义
的一组基,根据上面的定理和线性形式的性质,可以定义 下的行列式。
下的行列式。
其中的唯一性是因为如果有两个交替 线性形式满足条件,则它们的差在一组基上为0,从而恒等于0。于是,一组基上的一个向量组的行列式就是:
线性形式满足条件,则它们的差在一组基上为0,从而恒等于0。于是,一组基上的一个向量组的行列式就是:
定义:
确定了 上的一组基
上的一组基 后,向量组
后,向量组 在
在 下的行列式是:
下的行列式是:

- 其中
 是在
是在 下的展开[22]。
下的展开[22]。
可以见到这个定义与之前直观的定义是吻合的,它有时也被称作莱布尼兹公式。
设 与
与 是向量空间中的两组基,则将上面定理中的
是向量空间中的两组基,则将上面定理中的 改为
改为 就得到向量组在两组基下的行列式之间的关系:
就得到向量组在两组基下的行列式之间的关系:
 ,
,
設 為所有定義在系数域
為所有定義在系数域 上的
上的 矩陣的集合。將
矩陣的集合。將 矩陣
矩陣 (
( 的元素记为
的元素记为 )的
)的 列寫成
列寫成 ,
, 可以看作是
可以看作是 的正则基上的向量。矩阵
的正则基上的向量。矩阵 的行列式定义为向量组
的行列式定义为向量组 的行列式。这裡的向量都在
的行列式。这裡的向量都在 的正则基上展开,因此矩阵的行列式不依赖于基的选择。
的正则基上展开,因此矩阵的行列式不依赖于基的选择。
定义:
矩阵 的行列式
的行列式
 [23]
[23]
这样定义的矩阵 的行列式与向量组的行列式有同样的性质。单位矩阵的行列式为1,若矩阵的某几行线性相关,则它的行列式为零。
的行列式与向量组的行列式有同样的性质。单位矩阵的行列式为1,若矩阵的某几行线性相关,则它的行列式为零。
由莱布尼兹公式,可以证明矩阵行列式的一个重要性质:
定理:
一个矩阵的行列式等于它的转置矩阵的行列式: ,[24]
,[24]
也就是说矩阵的行列式既可以看作 个行向量的行列式,也可以看作
个行向量的行列式,也可以看作 个列向量的行列式。因此也可以通过行向量组来定义矩阵行列式,并且得到的定义是等价的。
个列向量的行列式。因此也可以通过行向量组来定义矩阵行列式,并且得到的定义是等价的。
设 是
是 维线性空间
维线性空间 到自身的线性变换(自同态),对于给定的一组基,可以定义线性变换在这组基下的行列式。
到自身的线性变换(自同态),对于给定的一组基,可以定义线性变换在这组基下的行列式。
f的变换矩阵满足![{\displaystyle \left[f(x_{1}),\dots ,f(x_{n})\right]=\left[f\right]_{B}\cdot \left[x_{1},\dots ,x_{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1b73609e0e3772b936ed8ff7ce42eb0f03e50c9) 也就是说对所有的向量组
也就是说对所有的向量组 ,
,
![{\displaystyle \det {}_{B}(f(x_{1}),\dots ,f(x_{n}))=\det \left([f]_{B}\right)\times \det {}_{B}(x_{1},\dots ,x_{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b635f7806f07618d11e21fe88041aa080b039922)
 。
。
可以证明,f在E的任意一组基下的变换矩阵的行列式都是相等的[25]。
证明:
考虑映射 使得
使得 被映射到
被映射到
 ,
,
 是一个交替n-线性形式,因此由前面证的定理,
是一个交替n-线性形式,因此由前面证的定理, 和
和 只相差一个系数。
只相差一个系数。
 。
。
而由变换矩阵的性质可以知道:![{\displaystyle \lambda =\det \left([f]_{B}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/506c08ea6f77e1aebef7fa1e59431196d5276173)
也就是说
![{\displaystyle \det {}_{B}(f(x_{1}),\dots ,f(x_{n}))=\det \left([f]_{B}\right)\times \det {}_{B}(x_{1},\dots ,x_{n})\qquad (1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd9a66dc1ef62cb1e85f0308fc1d610f13a5127d)
对于另外一组基 ,运用基变更公式,可以得到:
,运用基变更公式,可以得到:

![{\displaystyle {\begin{aligned}\det \left([f]_{B}\right)\times \det {}_{B}(x_{1},\dots ,x_{n})&=\det {}_{B}(f(x_{1}),\dots ,f(x_{n}))\\&=\det {}_{B}(B')\times \det {}_{B'}(f(x_{1}),\dots ,f(x_{n}))\\&=\det {}_{B}(B')\times \det \left([f]_{B'}\right)\times \det {}_{B'}(x_{1},\dots ,x_{n})\\&=\det \left([f]_{B'}\right)\times \det {}_{B}(x_{1},\dots ,x_{n})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/662e29af86a9eca9d36e81330e62ea728aa04a5b)
从而可以得出![{\displaystyle \det \left([f]_{B'}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86b3bdec3a97012f3f20fc79c3283f040655f44f) 等于
等于![{\displaystyle \det \left([f]_{B}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/661ec4ea02677ea3e17af840c1d745819742cf98) 。于是
。于是![{\displaystyle \det \left([f]_{B'}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86b3bdec3a97012f3f20fc79c3283f040655f44f) 是一个不依赖于基,只依赖于f的数。
是一个不依赖于基,只依赖于f的数。
因此线性变换的行列式定义可以修改为不依赖于基的形式:
前一节里对正方体做线性变换时, 是原来的基,
是原来的基, ,因此可以混淆向量组的行列式和线性变换的行列式[25]。
,因此可以混淆向量组的行列式和线性变换的行列式[25]。
特别地,行列式为1的线性变换保持向量组的行列式,它们构成一般线性群 的一个子群
的一个子群 ,称作特殊线性群[26]。可以证明,
,称作特殊线性群[26]。可以证明, 是由所有的错切生成的,即所有具有如下形式的矩阵代表的线性变换:
是由所有的错切生成的,即所有具有如下形式的矩阵代表的线性变换:

其中 是只在第
是只在第 行第
行第 列处系数取1,其余系数为0的矩阵。也就是说,错切变换保持向量组形成的“平行多面体”的体积[27]。同样,可以证明两个相似矩阵有相等的行列式[28]。
列处系数取1,其余系数为0的矩阵。也就是说,错切变换保持向量组形成的“平行多面体”的体积[27]。同样,可以证明两个相似矩阵有相等的行列式[28]。
以上的定义中都假设矩阵的系数取自域 中,实际上矩阵的系数可以是任意的交换环
中,实际上矩阵的系数可以是任意的交换环 ,这时有限维线性空间变为以
,这时有限维线性空间变为以 为基的自由
为基的自由 模,而相应的关于行列式的定义和性质依然成立(在可定义的范畴内)。如果矩阵系数是非交换环的话,以上的行列式定义将不再唯一。1845年,阿瑟·凯莱首次开始研究非交换环上行列式定义的问题。他注意到,对于系数是四元数(不可交换)的二阶行列式
模,而相应的关于行列式的定义和性质依然成立(在可定义的范畴内)。如果矩阵系数是非交换环的话,以上的行列式定义将不再唯一。1845年,阿瑟·凯莱首次开始研究非交换环上行列式定义的问题。他注意到,对于系数是四元数(不可交换)的二阶行列式

表达式 和
和 是不一样的。1926年,阿兰德·海廷和A.理查德森提出了非交换环上的行列式的不同定义。理查德森将二阶行列式定义为:
是不一样的。1926年,阿兰德·海廷和A.理查德森提出了非交换环上的行列式的不同定义。理查德森将二阶行列式定义为: ,而海廷则提倡使用
,而海廷则提倡使用 。两人都用归纳法定义了更高阶矩阵的行列式。1931年,奥斯丁·欧尔在一大类非交换环(后来命名为欧尔环)上定义了行列式的概念。最著名的非交换环上的行列式的定义当属让·迪厄多内的定义。迪厄多内是布尔巴基学派的代表成员之一,他将除环
。两人都用归纳法定义了更高阶矩阵的行列式。1931年,奥斯丁·欧尔在一大类非交换环(后来命名为欧尔环)上定义了行列式的概念。最著名的非交换环上的行列式的定义当属让·迪厄多内的定义。迪厄多内是布尔巴基学派的代表成员之一,他将除环 中的行列式定义在商域
中的行列式定义在商域![{\displaystyle \mathbb {K} /[\mathbb {K} ,\mathbb {K} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9259b3c625550df8ff1360629dcec81580a47a36) 上,而不是在
上,而不是在 中。这个定义下的行列式有接近交换环中行列式的性质。例如,迪尔多内的行列式可以保持行列式的乘法定理。而这种行列式与交换环中行列式的区别是:将矩阵的两行或两列互换后,行列式的值不变。[29]之后菲列克斯·别列金(Березин, Феликс Александрович)、佐藤幹夫等人对迪厄多内的定义进行了探究和扩展[30]。
中。这个定义下的行列式有接近交换环中行列式的性质。例如,迪尔多内的行列式可以保持行列式的乘法定理。而这种行列式与交换环中行列式的区别是:将矩阵的两行或两列互换后,行列式的值不变。[29]之后菲列克斯·别列金(Березин, Феликс Александрович)、佐藤幹夫等人对迪厄多内的定义进行了探究和扩展[30]。
行列式的一些基本性质,可以由它的多线性以及交替性推出。
- 在行列式中,一行(列)元素全為0,則此行列式的值為0[31]。

- 在行列式中,某一行(列)有公因子
 ,則可以提出
,則可以提出 [31]。
[31]。

- 在行列式中,某一行(列)的每個元素是兩數之和,則此行列式可拆分為兩個相加的行列式[31]。

- 行列式中的兩行(列)互換,改變行列式正負符號[31]。

- 在行列式中,有兩行(列)對應成比例或相同,則此行列式的值為0[31]。

- 將一行(列)的
 倍加進另一行(列)裡,行列式的值不變[31]。
倍加進另一行(列)裡,行列式的值不變[31]。

- 注意:一行(列)的
 倍加上另一行(列),行列式的值改變。
倍加上另一行(列),行列式的值改變。 
- 將行列式的行列互換,行列式的值不變,其中行列互換相當於轉置[31][32]。这个性质可以简单地记作

- 例如

- 行列式的乘法定理:方块矩陣的乘積的行列式等於行列式的乘積。
 。特别的,若将矩阵中的每一行每一列上的数都乘以一个常数
。特别的,若将矩阵中的每一行每一列上的数都乘以一个常数 ,那么所得到的行列式不是原来的
,那么所得到的行列式不是原来的 倍,而是
倍,而是 倍:[33]
倍:[33]
 。
。
- 以上的乘法公式还可以进一步推广为所谓柯西–比内公式,从而使得只要两个矩阵的乘积是方块矩阵,就有类似于以上的结果:假设
 是一个
是一个 矩阵,而
矩阵,而 是一个
是一个 矩阵。如果
矩阵。如果 是
是 中具有
中具有 个元素的子集
个元素的子集 ,我们记
,我们记 为
为 中列指标位于
中列指标位于 中的
中的 子矩阵。类似地,记
子矩阵。类似地,记 为
为 中行指标位于
中行指标位于 中的
中的 子矩阵。那么
子矩阵。那么

- 这里求遍
 中
中 个元素的所有可能子集
个元素的所有可能子集 (共有C(n,m)个)。
(共有C(n,m)个)。 - 如果
 ,即
,即 与
与 是同样大小的方块矩阵,则只有一个容许集合
是同样大小的方块矩阵,则只有一个容许集合 ,柯西–比内公式退化为通常行列式的乘法公式。如过
,柯西–比内公式退化为通常行列式的乘法公式。如过 则有
则有 容许集合
容许集合 ,这个公式退化为点积。如果
,这个公式退化为点积。如果 ,没有容许集合
,没有容许集合 ,约定行列式
,约定行列式 是零[34]。
是零[34]。
- 若
 是可逆矩陣,
是可逆矩陣, [35]。
[35]。 - 由行列式的乘法定理以及
 可以知道,行列式定义了一个从一般线性群
可以知道,行列式定义了一个从一般线性群 到
到 上的群同态[36]。
上的群同态[36]。 - 若将方块矩阵中的元素取共轭,得到的是矩阵的共轭矩阵。共轭矩阵的行列式值等於矩阵行列式值的共軛:
 [37]
[37] - 若兩個矩陣相似,那麼它們的行列式相同。这是因为两个相似的矩阵之间只相差一个基底变换,而行列式描述的是矩阵对应的线性映射对体积的影响,而不是体积,所以基底变换并不会影响行列式的值。用数学语言来说,就是:
- 如果兩個矩陣







 French
French Deutsch
Deutsch






















































































































![{\displaystyle \left[f\right]_{B}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d831914df02291d163b271f7dd768fbe23834f80)
![{\displaystyle \det f=\det \left([f]_{B}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9c801c2dd7f6a83e4b6e7eddee3d0f23caafbb8)
![{\displaystyle \left[f(x_{1}),\dots ,f(x_{n})\right]=\left[f\right]_{B}\cdot \left[x_{1},\dots ,x_{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1b73609e0e3772b936ed8ff7ce42eb0f03e50c9)

![{\displaystyle \det {}_{B}(f(x_{1}),\dots ,f(x_{n}))=\det \left([f]_{B}\right)\times \det {}_{B}(x_{1},\dots ,x_{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b635f7806f07618d11e21fe88041aa080b039922)






![{\displaystyle \lambda =\det \left([f]_{B}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/506c08ea6f77e1aebef7fa1e59431196d5276173)
![{\displaystyle \det {}_{B}(f(x_{1}),\dots ,f(x_{n}))=\det \left([f]_{B}\right)\times \det {}_{B}(x_{1},\dots ,x_{n})\qquad (1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd9a66dc1ef62cb1e85f0308fc1d610f13a5127d)

![{\displaystyle {\begin{aligned}\det \left([f]_{B}\right)\times \det {}_{B}(x_{1},\dots ,x_{n})&=\det {}_{B}(f(x_{1}),\dots ,f(x_{n}))\\&=\det {}_{B}(B')\times \det {}_{B'}(f(x_{1}),\dots ,f(x_{n}))\\&=\det {}_{B}(B')\times \det \left([f]_{B'}\right)\times \det {}_{B'}(x_{1},\dots ,x_{n})\\&=\det \left([f]_{B'}\right)\times \det {}_{B}(x_{1},\dots ,x_{n})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/662e29af86a9eca9d36e81330e62ea728aa04a5b)
![{\displaystyle \det \left([f]_{B'}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86b3bdec3a97012f3f20fc79c3283f040655f44f)
![{\displaystyle \det \left([f]_{B}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/661ec4ea02677ea3e17af840c1d745819742cf98)













![{\displaystyle \mathbb {K} /[\mathbb {K} ,\mathbb {K} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9259b3c625550df8ff1360629dcec81580a47a36)






























