泊松分布 概率质量函數
k ,发生次数。该函数只定义在k 为整数的时候。连接线是只为了指导视觉。 累積分布函數
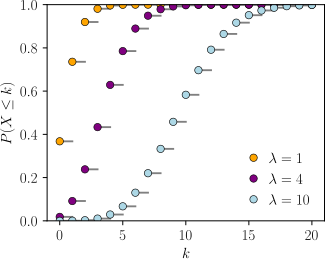
k ,发生次数。CDF在整数k 处不连续,且在其他任何地方都是水平的,因为服从泊松分布的变量只针对整数值。 参数 λ > 0(实数 ) 值域 k ∈ { 0 , 1 , 2 , 3 , ⋯ } {\displaystyle k\in \{0,1,2,3,\cdots \}} 概率质量函数 λ k k ! e − λ {\displaystyle {\frac {\lambda ^{k}}{k!}}e^{-\lambda }} 累積分布函數 Γ ( ⌊ k + 1 ⌋ , λ ) ⌊ k ⌋ ! {\displaystyle {\frac {\Gamma (\lfloor k+1\rfloor ,\lambda )}{\lfloor k\rfloor !}}} e − λ ∑ i = 0 ⌊ k ⌋ λ i i ! {\displaystyle e^{-\lambda }\sum _{i=0}^{\lfloor k\rfloor }{\frac {\lambda ^{i}}{i!}}\ } Q ( ⌊ k + 1 ⌋ , λ ) {\displaystyle Q(\lfloor k+1\rfloor ,\lambda )}
(对于 k ≥ 0 {\displaystyle k\geq 0} Γ ( x , y ) {\displaystyle \Gamma (x,y)} 不完全Γ函数 , ⌊ k ⌋ {\displaystyle \lfloor k\rfloor } 高斯符号 ,Q是规则化Γ函数) 期望值 λ {\displaystyle \lambda } 中位數 ≈ ⌊ λ + 1 / 3 − 0.02 / λ ⌋ {\displaystyle \approx \lfloor \lambda +1/3-0.02/\lambda \rfloor } 眾數 ⌈ λ ⌉ − 1 , ⌊ λ ⌋ {\displaystyle \lceil \lambda \rceil -1,\lfloor \lambda \rfloor } 方差 λ {\displaystyle \lambda } 偏度 λ − 1 / 2 {\displaystyle \lambda ^{-1/2}} 峰度 λ − 1 {\displaystyle \lambda ^{-1}} 熵 λ [ 1 − log ( λ ) ] + e − λ ∑ k = 0 ∞ λ k log ( k ! ) k ! {\displaystyle \lambda [1-\log(\lambda )]+e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\log(k!)}{k!}}} λ {\displaystyle \lambda }
1 2 log ( 2 π e λ ) − 1 12 λ − 1 24 λ 2 − {\displaystyle {\frac {1}{2}}\log(2\pi e\lambda )-{\frac {1}{12\lambda }}-{\frac {1}{24\lambda ^{2}}}-} 19 360 λ 3 + O ( 1 λ 4 ) {\displaystyle \qquad {\frac {19}{360\lambda ^{3}}}+O\left({\frac {1}{\lambda ^{4}}}\right)} 矩生成函数 exp ( λ ( e t − 1 ) ) {\displaystyle \exp(\lambda (e^{t}-1))} 特徵函数 exp ( λ ( e i t − 1 ) ) {\displaystyle \exp(\lambda (e^{it}-1))} 概率母函数 exp ( λ ( z − 1 ) ) {\displaystyle \exp(\lambda (z-1))}
泊松分布 (法語:loi de Poisson ;英語:Poisson distribution )又稱Poisson分布 、帕松分布 、布瓦松分布 、布阿松分布 、普阿松分布 、波以松分布 、卜氏分布 、帕松小數法則 (Poisson law of small numbers),是一種統計 與概率 學裡常見到的離散機率分布 ,由法國 數學家西莫恩·德尼·泊松 在1838年時發表。
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,电话交换机 接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害 发生的次数、DNA序列的变异数、放射性原子核的衰变数、雷射 的光子數分布等等。(單位時間內發生的次數,可以看作事件發生的頻率,類似物理的頻率 f {\displaystyle f}
泊松分布的機率質量函数 为:
P ( X = k ) = e − λ λ k k ! {\displaystyle P(X=k)={\frac {e^{-\lambda }\lambda ^{k}}{k!}}} 泊松分布的参数 λ {\displaystyle \lambda }
若 X {\displaystyle X} λ {\displaystyle \lambda } X ∼ π ( λ ) {\displaystyle X\sim \pi (\lambda )} X ∼ Poisson ( λ ) {\displaystyle X\sim {\text{Poisson}}(\lambda )}
如果以下假设成立,则适用泊松分布:
k是一个非负整数,是某个事件在某个时间间隔内发生的次数。 一个事件的发生不会影响第二个事件的概率。 事件发生的平均速率与任何事件的发生无关。 两个事件不可能在同一时刻发生。 如果这些条件成立,则k是泊松随机变量;k的分布是泊松分布。
服从泊松分布的随机变量 ,其数学期望 与方差 相等,同为参数 λ {\displaystyle \lambda } E ( X ) = V ( X ) = λ {\displaystyle E(X)=V(X)=\lambda } 兩個獨立且服从泊松分布的随机变量 ,其和仍然服从泊松分布。更精確地說,若 X ∼ Poisson ( λ 1 ) {\displaystyle X\sim {\text{Poisson}}(\lambda _{1})} Y ∼ Poisson ( λ 2 ) {\displaystyle Y\sim {\text{Poisson}}(\lambda _{2})} X + Y ∼ Poisson ( λ 1 + λ 2 ) {\displaystyle X+Y\sim {\text{Poisson}}(\lambda _{1}+\lambda _{2})} Raikov定理 其動差母函數 为: M X ( t ) = E [ e t X ] = ∑ x = 0 ∞ e t x e − λ λ x x ! = e − λ ∑ x = 0 ∞ ( e t λ ) x x ! = e λ ( e t − 1 ) {\displaystyle M_{X}(t)=E[e^{tX}]=\sum _{x=0}^{\infty }e^{tx}{\frac {e^{-\lambda }\lambda ^{x}}{x!}}=e^{-\lambda }\sum _{x=0}^{\infty }{\frac {({e^{t}}\lambda )^{x}}{x!}}=e^{{\lambda }(e^{t}-1)}} 期望值:(倒數第三至第二是使用泰勒展開式 )
E ( X ) = ∑ i = 0 ∞ i P ( X = i ) = ∑ i = 1 ∞ i e − λ λ i i ! = λ e − λ ∑ i = 1 ∞ λ i − 1 ( i − 1 ) ! = λ e − λ ∑ i = 0 ∞ λ i i ! = λ e − λ e λ = λ {\displaystyle {\begin{aligned}\mathrm {E} (X)&=\sum _{i=0}^{\infty }\displaystyle iP(X=i)\\&=\sum _{i=1}^{\infty }\displaystyle i{e^{-\lambda }\lambda ^{i} \over i!}\\&=\lambda e^{-\lambda }\sum _{i=1}^{\infty }\displaystyle {\lambda ^{i-1} \over (i-1)!}\\&=\lambda e^{-\lambda }\sum _{i=0}^{\infty }\displaystyle {\lambda ^{i} \over i!}\\&=\lambda e^{-\lambda }e^{\lambda }\\&=\lambda \end{aligned}}}
E ( X 2 ) = ∑ i = 0 ∞ i 2 P ( X = i ) = ∑ i = 1 ∞ i 2 e − λ λ i i ! = λ e − λ ∑ i = 1 ∞ i λ i − 1 ( i − 1 ) ! = λ e − λ ∑ i = 1 ∞ 1 ( i − 1 ) ! d d λ ( λ i ) = λ e − λ d d λ [ ∑ i = 1 ∞ λ i ( i − 1 ) ! ] = λ e − λ d d λ [ λ ∑ i = 1 ∞ λ i − 1 ( i − 1 ) ! ] = λ e − λ d d λ ( λ e λ ) = λ e − λ ( e λ + λ e λ ) = λ + λ 2 {\displaystyle {\begin{aligned}\mathrm {E} (X^{2})&=\sum _{i=0}^{\infty }\displaystyle i^{2}P(X=i)\\&=\sum _{i=1}^{\infty }\displaystyle i^{2}{e^{-\lambda }\lambda ^{i} \over i!}\\&=\lambda e^{-\lambda }\sum _{i=1}^{\infty }\displaystyle {i\lambda ^{i-1} \over (i-1)!}\\&=\lambda e^{-\lambda }\sum _{i=1}^{\infty }\displaystyle {1 \over (i-1)!}{d \over d\lambda }(\lambda ^{i})\\&=\lambda e^{-\lambda }{d \over d\lambda }\left[\sum _{i=1}^{\infty }\displaystyle {\lambda ^{i} \over (i-1)!}\right]\\&=\lambda e^{-\lambda }{d \over d\lambda }\left[\lambda \sum _{i=1}^{\infty }\displaystyle {\lambda ^{i-1} \over (i-1)!}\right]\\&=\lambda e^{-\lambda }{d \over d\lambda }(\lambda e^{\lambda })=\lambda e^{-\lambda }(e^{\lambda }+\lambda e^{\lambda })=\lambda +\lambda ^{2}\end{aligned}}}
我們可以得到: V a r ( X ) = ( λ + λ 2 ) − λ 2 = λ {\displaystyle Var(X)=(\lambda +\lambda ^{2})-\lambda ^{2}=\lambda }
如同性質: E ( X ) = V a r ( X ) = λ {\displaystyle E(X)=Var(X)=\lambda } σ X = λ {\displaystyle \sigma _{X}={\sqrt {\lambda }}}
相互獨立的卜瓦松分佈隨機變數之和仍服從卜瓦松分佈:
X ∼ Poisson ( λ 1 ) , Y ∼ Poisson ( λ 2 ) . {\displaystyle X\sim {\text{Poisson}}(\lambda _{1}),Y\sim {\text{Poisson}}(\lambda _{2}).}
P ( X = k 1 ) = λ 1 k 1 e − λ 1 k 1 ! , P ( Y = k 2 ) = λ 2 k 2 e − λ 2 k 2 ! . {\displaystyle P(X=k_{1})={\dfrac {\lambda _{1}^{k_{1}}e^{-\lambda _{1}}}{k_{1}!}},P(Y=k_{2})={\dfrac {\lambda _{2}^{k_{2}}e^{-\lambda _{2}}}{k_{2}!}}.}
P ( X + Y = k ) = ∑ i = 0 k P ( X = i ) P ( Y = k − i ) = ∑ i = 0 k λ 1 i λ 2 k − i e − ( λ 1 + λ 2 ) i ! ( k − i ) ! = e − ( λ 1 + λ 2 ) k ! ∑ i = 0 k C k i λ 1 i λ 2 k − i = e − ( λ 1 + λ 2 ) ( λ 1 + λ 2 ) k k ! {\displaystyle {\begin{aligned}P(X+Y=k)&=\sum _{i=0}^{k}P(X=i)P(Y=k-i)\\&=\sum _{i=0}^{k}{\frac {\lambda _{1}^{i}\lambda _{2}^{k-i}e^{-(\lambda _{1}+\lambda _{2})}}{i!(k-i)!}}\\&={\frac {e^{-(\lambda _{1}+\lambda _{2})}}{k!}}\sum _{i=0}^{k}C_{k}^{i}\lambda _{1}^{i}\lambda _{2}^{k-i}\\&={\frac {e^{-(\lambda _{1}+\lambda _{2})}(\lambda _{1}+\lambda _{2})^{k}}{k!}}\end{aligned}}}
X + Y ∼ Poisson ( λ 1 + λ 2 ) {\displaystyle X+Y\sim {\text{Poisson}}(\lambda _{1}+\lambda _{2})}
在二项分布 的伯努利试验 中,如果试验次数 n {\displaystyle n} p {\displaystyle p} λ = n p {\displaystyle \lambda =np}
证明如下。首先,回顾自然對數 e {\displaystyle e}
lim n → ∞ ( 1 − λ n ) n = e − λ , {\displaystyle \lim _{n\to \infty }\left(1-{\lambda \over n}\right)^{n}=e^{-\lambda },} 二项分布的定义:
P ( X = k ) = ( n k ) p k ( 1 − p ) n − k {\displaystyle P(X=k)={n \choose k}p^{k}(1-p)^{n-k}} 如果令 p = λ n {\displaystyle p={\frac {\lambda }{n}}} n {\displaystyle n} P {\displaystyle P}
lim n → ∞ P ( X = k ) = lim n → ∞ ( n k ) p k ( 1 − p ) n − k = lim n → ∞ n ! ( n − k ) ! k ! ( λ n ) k ( 1 − λ n ) n − k = lim n → ∞ [ n ! n k ( n − k ) ! ] ⏟ F ( λ k k ! ) ( 1 − λ n ) n ⏟ → exp ( − λ ) ( 1 − λ n ) − k ⏟ → 1 = lim n → ∞ [ ( 1 − 1 n ) ( 1 − 2 n ) … ( 1 − k − 1 n ) ] ⏟ → 1 ( λ k k ! ) ( 1 − λ n ) n ⏟ → exp ( − λ ) ( 1 − λ n ) − k ⏟ → 1 = ( λ k k ! ) exp ( − λ ) {\displaystyle {\begin{aligned}\lim _{n\to \infty }P(X=k)&=\lim _{n\to \infty }{n \choose k}p^{k}(1-p)^{n-k}\\&=\lim _{n\to \infty }{n! \over (n-k)!k!}\left({\lambda \over n}\right)^{k}\left(1-{\lambda \over n}\right)^{n-k}\\&=\lim _{n\to \infty }\underbrace {\left[{\frac {n!}{n^{k}\left(n-k\right)!}}\right]} _{F}\left({\frac {\lambda ^{k}}{k!}}\right)\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{n}} _{\to \exp \left(-\lambda \right)}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{-k}} _{\to 1}\\&=\lim _{n\to \infty }\underbrace {\left[\left(1-{\frac {1}{n}}\right)\left(1-{\frac {2}{n}}\right)\ldots \left(1-{\frac {k-1}{n}}\right)\right]} _{\to 1}\left({\frac {\lambda ^{k}}{k!}}\right)\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{n}} _{\to \exp \left(-\lambda \right)}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{-k}} _{\to 1}\\&=\left({\frac {\lambda ^{k}}{k!}}\right)\exp \left(-\lambda \right)\end{aligned}}} 给定 n {\displaystyle n} k i {\displaystyle k_{i}} λ {\displaystyle \lambda } 最大似然估计 值,列出对数似然函数:
L ( λ ) = ln ∏ i = 1 n f ( k i ∣ λ ) = ∑ i = 1 n ln ( e − λ λ k i k i ! ) = − n λ + ( ∑ i = 1 n k i ) ln ( λ ) − ∑ i = 1 n ln ( k i ! ) . {\displaystyle {\begin{aligned}L(\lambda )&=\ln \prod _{i=1}^{n}f(k_{i}\mid \lambda )\\&=\sum _{i=1}^{n}\ln \!\left({\frac {e^{-\lambda }\lambda ^{k_{i}}}{k_{i}!}}\right)\\&=-n\lambda +\left(\sum _{i=1}^{n}k_{i}\right)\ln(\lambda )-\sum _{i=1}^{n}\ln(k_{i}!).\end{aligned}}} d d λ L ( λ ) = 0 ⟺ − n + ( ∑ i = 1 n k i ) 1 λ = 0. {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} \lambda }}L(\lambda )=0\iff -n+\left(\sum _{i=1}^{n}k_{i}\right){\frac {1}{\lambda }}=0.\!} 解得λ 从而得到一个驻点 (stationary point):
λ ^ M L E = 1 n ∑ i = 1 n k i . {\displaystyle {\widehat {\lambda }}_{\mathrm {MLE} }={\frac {1}{n}}\sum _{i=1}^{n}k_{i}.\!} 检查函数 L {\displaystyle L} λ {\displaystyle \lambda } k i {\displaystyle k_{i}} L {\displaystyle L}
∂ 2 L ∂ λ 2 = ∑ i = 1 n − λ − 2 k i {\displaystyle {\frac {\partial ^{2}L}{\partial \lambda ^{2}}}=\sum _{i=1}^{n}-\lambda ^{-2}k_{i}} 对某公共汽车站的客流做调查,统计了某天上午10:30到11:47来到候车的乘客情况。假定来到候车的乘客各批(每批可以是1人也可以是多人)是互相独立发生的。观察每20秒区间来到候车的乘客批次,共观察77分钟*3=231次,共得到230个观察记录。其中来到0批、1批、2批、3批、4批及4批以上的观察记录分别是100次、81次、34次、9次、6次。使用极大似真估计(MLE),得到 λ {\displaystyle \lambda } 81 × 1 + 34 × 2 + 9 × 3 + 6 × 4 230 ≈ 0.87 {\displaystyle {\frac {81\times 1+34\times 2+9\times 3+6\times 4}{230}}\approx 0.87}
一个用来生成随机泊松分布的数字(伪随机数抽样)的简单算法,已经由高德纳 给出(见下文参考):
algorithm poisson random number (Knuth) : init : Let L ← e −λ , k ← 0 and p ← 1. do : k ← k + 1. Generate uniform random number u in [0,1] and let p ← p×u. while p > L. return k − 1. 尽管简单,但复杂度是线性的,在返回的值 k {\displaystyle k} λ {\displaystyle \lambda } λ {\displaystyle \lambda } e − λ {\displaystyle e^{-\lambda }} λ {\displaystyle \lambda } 拒绝采样 ,另一种是采用泊松分布的高斯近似。
对于很小的 λ {\displaystyle \lambda } u {\displaystyle u}
algorithm Poisson generator based upon the inversion by sequential search :[ 1] init : Let x ← 0, p ← e −λ , s ← p. Generate uniform random number u in [0,1]. do : x ← x + 1. p ← p * λ / x. s ← s + p. while u > s. return x. Guerriero V. Power Law Distribution: Method of Multi-scale Inferential Statistics . Journal of Modern Mathematics Frontier (JMMF). 2012, 1 : 21–28 [2017-10-30 ] . (原始内容 存档于2018-02-21). Joachim H. Ahrens, Ulrich Dieter. Computer Methods for Sampling from Gamma, Beta, Poisson and Binomial Distributions. Computing. 1974, 12 (3): 223–246. doi:10.1007/BF02293108 Joachim H. Ahrens, Ulrich Dieter. Computer Generation of Poisson Deviates . ACM Transactions on Mathematical Software. 1982, 8 (2): 163–179. doi:10.1145/355993.355997 Ronald J. Evans, J. Boersma, N. M. Blachman, A. A. Jagers. The Entropy of a Poisson Distribution: Problem 87-6. SIAM Review. 1988, 30 (2): 314–317. doi:10.1137/1030059 Donald E. Knuth. Seminumerical Algorithms. The Art of Computer Programming. Volume 2. Addison Wesley . 1969.



 French
French Deutsch
Deutsch












![{\displaystyle \lambda [1-\log(\lambda )]+e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\log(k!)}{k!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf6cf37058d59e89453fd5bf9a1ece59a8c81d1a)














![{\displaystyle M_{X}(t)=E[e^{tX}]=\sum _{x=0}^{\infty }e^{tx}{\frac {e^{-\lambda }\lambda ^{x}}{x!}}=e^{-\lambda }\sum _{x=0}^{\infty }{\frac {({e^{t}}\lambda )^{x}}{x!}}=e^{{\lambda }(e^{t}-1)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07027a2d97d52986d99b0a73c00430e95cdbdc8a)

![{\displaystyle {\begin{aligned}\mathrm {E} (X^{2})&=\sum _{i=0}^{\infty }\displaystyle i^{2}P(X=i)\\&=\sum _{i=1}^{\infty }\displaystyle i^{2}{e^{-\lambda }\lambda ^{i} \over i!}\\&=\lambda e^{-\lambda }\sum _{i=1}^{\infty }\displaystyle {i\lambda ^{i-1} \over (i-1)!}\\&=\lambda e^{-\lambda }\sum _{i=1}^{\infty }\displaystyle {1 \over (i-1)!}{d \over d\lambda }(\lambda ^{i})\\&=\lambda e^{-\lambda }{d \over d\lambda }\left[\sum _{i=1}^{\infty }\displaystyle {\lambda ^{i} \over (i-1)!}\right]\\&=\lambda e^{-\lambda }{d \over d\lambda }\left[\lambda \sum _{i=1}^{\infty }\displaystyle {\lambda ^{i-1} \over (i-1)!}\right]\\&=\lambda e^{-\lambda }{d \over d\lambda }(\lambda e^{\lambda })=\lambda e^{-\lambda }(e^{\lambda }+\lambda e^{\lambda })=\lambda +\lambda ^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67cfdcfdefe078c4ae07a091d4ec9cc56b007d67)














![{\displaystyle {\begin{aligned}\lim _{n\to \infty }P(X=k)&=\lim _{n\to \infty }{n \choose k}p^{k}(1-p)^{n-k}\\&=\lim _{n\to \infty }{n! \over (n-k)!k!}\left({\lambda \over n}\right)^{k}\left(1-{\lambda \over n}\right)^{n-k}\\&=\lim _{n\to \infty }\underbrace {\left[{\frac {n!}{n^{k}\left(n-k\right)!}}\right]} _{F}\left({\frac {\lambda ^{k}}{k!}}\right)\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{n}} _{\to \exp \left(-\lambda \right)}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{-k}} _{\to 1}\\&=\lim _{n\to \infty }\underbrace {\left[\left(1-{\frac {1}{n}}\right)\left(1-{\frac {2}{n}}\right)\ldots \left(1-{\frac {k-1}{n}}\right)\right]} _{\to 1}\left({\frac {\lambda ^{k}}{k!}}\right)\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{n}} _{\to \exp \left(-\lambda \right)}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{-k}} _{\to 1}\\&=\left({\frac {\lambda ^{k}}{k!}}\right)\exp \left(-\lambda \right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f3305a795ed8b2ce32f86487f67b44ecd5f69cb)











