Équations de Navier-Stokes — Wikipédia

En mécanique des fluides, les équations de Navier-Stokes sont des équations aux dérivées partielles non linéaires qui décrivent le mouvement des fluides newtoniens (donc des gaz et de la majeure partie des liquides^[a]). La résolution de ces équations modélisant un fluide comme un milieu continu à une seule phase est difficile, et l'existence mathématique de solutions des équations de Navier-Stokes n'est pas démontrée. Mais elles permettent souvent, par une résolution approchée, de proposer une modélisation de nombreux phénomènes, comme les courants océaniques et des mouvements des masses d'air de l'atmosphère pour les météorologistes, le comportement des gratte-ciel ou des ponts sous l'action du vent pour les architectes et les ingénieurs, ou encore celui des avions, des trains ou des voitures à grande vitesse pour leurs bureaux d'études concepteurs, ainsi que l'écoulement de l'eau dans un tuyau et de nombreux autres phénomènes d'écoulement de divers fluides.

Ces équations sont nommées ainsi pour honorer les travaux de deux scientifiques du XIX^e siècle : le mathématicien et ingénieur des Ponts Henri Navier, qui le premier a introduit la notion de viscosité dans les équations d'Euler en 1822^[1], et le physicien George Gabriel Stokes, qui a donné sa forme définitive à l'équation de conservation de la quantité de mouvement en 1845^[2],[3]. Entre-temps, divers scientifiques ont contribué à l'avancement du sujet : Augustin Louis Cauchy^[4], Siméon Denis Poisson en 1829^[5] et Adhémar Barré de Saint-Venant en 1843.

Pour un gaz peu dense, il est possible de trouver une solution approchée de l’équation de Boltzmann, décrivant le comportement statistique des particules dans le cadre de la théorie cinétique des gaz. Ainsi, la méthode de Chapman-Enskog, due à Sydney Chapman et David Enskog en 1916 et 1917, permet de généraliser les équations de Navier-Stokes à un milieu comportant plusieurs espèces et de calculer l'expression des flux de masse (équations de Stefan-Maxwell incluant l'effet Soret), de quantité de mouvement (en donnant l'expression du tenseur de pression) et d'énergie en montrant l'existence de l'effet Dufour. Cette méthode permet également de calculer les coefficients de transport à partir des potentiels d'interaction moléculaires.

La résolution mathématiquement rigoureuse des équations de Navier-Stokes constitue l'un des problèmes du prix du millénaire.

Cet article décrit diverses variantes des équations valables pour des milieux de composition homogène, les problèmes liés à la diffusion et aux réactions chimiques n'y sont pas abordés^[6].

Lois de conservation[modifier | modifier le code]

Notations et relations utilisées[modifier | modifier le code]

On utilise les notations conformes à la norme ISO/CEI 80000-2^[7]

• Les caractères en gras sans serif comme ${\displaystyle {\mathsf {T}}}$ désignent des tenseurs.
• ${\displaystyle {\vec {\nabla }}={\frac {\partial }{\partial x}}{\vec {u_{x}}}+{\frac {\partial }{\partial y}}{\vec {u_{y}}}+{\frac {\partial }{\partial z}}{\vec {u_{z}}}}$ est l'opérateur nabla exprimé dans un système de coordonnées cartésiennes.
• ${\displaystyle {\vec {\nabla }}\phi ={\frac {\partial \phi }{\partial x}}{\vec {u_{x}}}+{\frac {\partial \phi }{\partial y}}{\vec {u_{y}}}+{\frac {\partial \phi }{\partial z}}{\vec {u_{z}}}}$ est l'opérateur gradient exprimé dans un système de coordonnées cartésiennes.
• ${\displaystyle {\vec {\nabla }}\cdot {\vec {A}}={{\partial A_{x}} \over \partial x}+{{\partial A_{y}} \over \partial y}+{{\partial A_{z}} \over \partial z}}$ est l'opérateur divergence exprimé dans un système de coordonnées cartésiennes.
• ${\displaystyle {\vec {\nabla }}\times {\vec {A}}={\bigg (}{\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}{\bigg )}{\vec {u_{x}}}+{\bigg (}{\frac {\partial A_{x}}{\partial z}}-{\frac {\partial A_{z}}{\partial x}}{\bigg )}{\vec {u_{y}}}+{\bigg (}{\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}{\bigg )}{\vec {u_{z}}}}$ désigne l'opérateur rotationnel exprimé dans un système de coordonnées cartésiennes. Il est parfois noté ${\displaystyle {\vec {\nabla }}\wedge {\vec {A}}}$.
• ${\displaystyle \nabla ^{2}\phi ={\vec {\nabla }}\cdot ({\vec {\nabla }}\phi )=\Delta \phi ={\frac {\partial ^{2}\phi }{\partial x^{2}}}+{\frac {\partial ^{2}\phi }{\partial y^{2}}}+{\frac {\partial ^{2}\phi }{\partial z^{2}}}}$ est l'opérateur laplacien exprimé dans un système de coordonnées cartésiennes.
• ${\displaystyle \Delta {\vec {A}}}$ est le laplacien vectoriel, soit le vecteur dont chaque composante est le laplacien de la même composante de ${\displaystyle {\vec {A}}}$.

Note : ${\displaystyle \Delta {\vec {A}}}$ diffère de ${\displaystyle {\vec {\nabla }}^{2}{\vec {A}}={\vec {\nabla }}({\vec {\nabla }}\cdot {\vec {A}})}$. Toutefois, ${\displaystyle \nabla ^{2}{\vec {A}}=\Delta {\vec {A}}}$ ne prête plus à confusion.

• Le produit dyadique de deux vecteurs s'écrit

${\displaystyle {\mathsf {T}}={\vec {A}}{\vec {B}}={\vec {A}}\times {\vec {B}}^{T}}$

où × est le produit matriciel.

• Le produit doublement contracté : est l'opérateur défini par :

${\displaystyle \alpha ={\mathsf {T}}_{1}:{\mathsf {T}}_{2}={\textrm {Tr}}({\mathsf {T}}_{1}\cdot {\mathsf {T}}_{2}^{T})}$

où Tr représente l'opérateur trace.

Quelques identités vectorielles utiles pour cet article (les deux dernières généralisent la notion de divergence aux tenseurs de rang deux) :

${\displaystyle {\begin{array}{rcl}{\vec {\nabla }}\times ({\vec {\nabla }}\,\phi )&=&0\\[0.2em]{\vec {\nabla }}\cdot ({\vec {\nabla }}\times {\vec {A}})&=&0\\[0.2em]({\vec {\nabla }}\times {\vec {A}})\times {\vec {A}}&=&({\vec {A}}\cdot {\vec {\nabla }})\,{\vec {A}}-{\vec {\nabla }}A\,{\vec {A}}\\[0.2em]{\vec {\nabla }}A\,{\vec {A}}&=&{\frac {1}{2}}\,{\vec {\nabla }}\,({\vec {A}}\cdot {\vec {A}})\\[0.2em]{\vec {\nabla }}\cdot ({\vec {\nabla }}\phi )&=&{\vec {\nabla }}^{2}\phi \\[0.2em]{\vec {\nabla }}\times ({\vec {\nabla }}\times {\vec {A}})&=&{\vec {\nabla }}({\vec {\nabla }}\cdot {\vec {A}})-\Delta {\vec {A}}\\[0.2em]{\vec {\nabla }}\cdot (\alpha \,{\mathsf {T}}\,)&=&{\vec {\nabla }}\alpha \cdot {\mathsf {T}}\,+({\vec {\nabla }}\cdot {\mathsf {T}}\,)\,\alpha \\[0.2em]{\vec {\nabla }}\cdot ({\vec {A}}{\vec {B}})&=&({\vec {B}}\cdot {\vec {\nabla }})\,{\vec {A}}+{\vec {A}}\,({\vec {\nabla }}\cdot {\vec {B}})\\[0.2em]\end{array}}}$

Loi de conservation[modifier | modifier le code]

On peut définir une loi de conservation pour une variable extensive ${\displaystyle \Phi }$ de densité ϕ entraînée à la vitesse ${\displaystyle {\vec {V}}}$ et comportant un terme de production volumique S par :

${\displaystyle {\frac {\partial \phi }{\partial t}}+\nabla \cdot (\phi {\vec {V}})=S}$.

Formulation eulérienne[modifier | modifier le code]

La formulation la plus utilisée fait appel à un référentiel fixe naturel lorsque l'on traite un problème stationnaire ou instationnaire dans lequel le domaine de calcul est connu à l'avance. On fait alors appel aux variables eulériennes.

On obtient les équations de Navier-Stokes en appliquant la relation de conservation ci-dessus à la masse volumique ρ, à la quantité de mouvement ${\displaystyle \rho \,{\vec {V}}}$ et à l'énergie totale ρ E^[8].

• Équation de continuité (équation de bilan de la masse)

  ${\displaystyle {\frac {\partial \rho }{\partial t}}+{\vec {\nabla }}\cdot (\rho {\vec {V}})=0}$

• Équation de bilan de la quantité de mouvement

  ${\displaystyle {\begin{array}{rcl}{\dfrac {\partial (\rho {\vec {V}})}{\partial t}}+{\vec {\nabla }}\cdot \left(\rho {\vec {V}}{\vec {V}}\right)&=&{\vec {\nabla }}\cdot {\mathsf {P}}+\rho {\vec {g}}\\[0.5em]&=&-{\vec {\nabla }}p+{\vec {\nabla }}\cdot {\mathsf {\Sigma }}+\rho {\vec {g}}\end{array}}}$

• Équation de bilan de l'énergie

  ${\displaystyle {\frac {\partial (\rho E)}{\partial t}}+{\vec {\nabla }}\cdot (\rho E{\vec {V}})={\vec {\nabla }}\cdot \left({\mathsf {P}}\cdot {\vec {V}}\right)+\rho {\vec {g}}\cdot {\vec {V}}+{\vec {\nabla }}\cdot {\vec {q}}+{\vec {\nabla }}\cdot {\vec {q}}_{R}}$

Dans ces équations :

• t représente le temps (unité SI : s) ;
• ρ désigne la masse volumique du fluide (unité SI : kg m⁻³) ;
• ${\displaystyle {\vec {V}}}$ désigne la vitesse eulérienne d'une particule fluide (unité SI : m s⁻¹) ;
• ${\displaystyle {\mathsf {P}}}$ désigne le tenseur des contraintes (ou tenseur de pression) qui, si on néglige le rayonnement, se décompose en :

${\displaystyle {\mathsf {P}}={\mathsf {\Sigma }}-p{\mathsf {I}}}$ ;

• ${\displaystyle {\mathsf {\Sigma }}}$ désigne le tenseur des contraintes visqueuses (unité SI : Pa) ;
• ${\displaystyle {\mathsf {I}}}$ désigne le tenseur unité ;
• p désigne la pression thermodynamique (unité SI : Pa) ;
• ${\displaystyle {\vec {g}}}$ désigne la gravité ou toute autre force massique extérieure (unité SI : m s⁻²) ;
• E désigne l'énergie totale par unité de masse (unité SI : J kg⁻¹) ; elle s'exprime en fonction de l'énergie interne par unité de masse e par :

${\displaystyle E=e+{\frac {||{\vec {V}}||^{2}}{2}}}$ ;

• ${\displaystyle {\vec {q}}}$ désigne le flux de chaleur dû à la conduction thermique (unité SI : J m⁻² s⁻¹) ;
• ${\displaystyle {\vec {q}}_{R}}$ désigne le flux de chaleur dû au rayonnement (unité SI : J m⁻² s⁻¹).

Afin de clore le système il est nécessaire de décrire p, Σ, et ${\displaystyle {\vec {q}}}$ à partir d'hypothèses sur le fluide considéré. ${\displaystyle {\vec {q}}_{R}}$ est quant à lui l'objet d'un calcul de transfert radiatif éventuellement couplé à la résolution des équations de Navier-Stokes.

Quelques variations autour du système d'équations[modifier | modifier le code]

• On peut exprimer différemment l'équation de quantité de mouvement en remarquant que :

${\displaystyle {\frac {\partial \left(\rho {\vec {V}}\right)}{\partial t}}+{\vec {\nabla }}\cdot \left(\rho {\vec {V}}{\vec {V}}\right)=\rho \left[{\frac {\partial {\vec {V}}}{\partial t}}+({\vec {V}}\cdot {\vec {\nabla }}){\vec {V}}\right]}$.

L'équation alors obtenue s'interprète comme la deuxième loi de Newton, en remarquant que le terme ${\displaystyle {\frac {\partial {\vec {V}}}{\partial t}}+({\vec {V}}\cdot {\vec {\nabla }}){\vec {V}}={\frac {D{\vec {V}}}{Dt}}}$ décrit l’accélération des particules du fluide.

• Il est possible d'exprimer la conservation de l'énergie sous forme équivalente en transférant au premier membre le terme correspondant à la pression :

${\displaystyle {\frac {\partial (\rho E)}{\partial t}}+{\vec {\nabla }}\cdot [(\rho E+p){\vec {V}}]={\vec {\nabla }}\cdot \left({\mathsf {\Sigma }}\cdot {\vec {V}}\right)+\rho {\vec {g}}\cdot {\vec {V}}+{\vec {\nabla }}\cdot {\vec {q}}+{\vec {q}}_{R}}$.

Le terme ρ E + p peut être remplacé par ${\displaystyle \rho \left(h+{\frac {||{\vec {V}}||^{2}}{2}}\right)}$ où h = e + p/ρ est l'enthalpie massique.

• En multipliant scalairement l'équation de quantité de mouvement écrite comme ci-dessus par la vitesse on obtient une loi de conservation pour l'énergie cinétique :

${\displaystyle \rho \left[{\frac {\partial }{\partial t}}\left({\frac {||{\vec {V}}||^{2}}{2}}\right)+{\vec {V}}\cdot {\vec {\nabla }}\left({\frac {||{\vec {V}}||^{2}}{2}}\right)\right]=({\vec {\nabla }}\cdot {\mathsf {P}})\cdot {\vec {V}}+\rho {\vec {g}}\cdot {\vec {V}}}$.

• En soustrayant cette équation de l'équation de conservation de l'énergie, en utilisant l'équation de conservation de la masse et l'identité

${\displaystyle {\vec {\nabla }}\cdot ({\mathsf {P}}\cdot {\vec {V}})-({\vec {\nabla }}\cdot {\mathsf {P}})\cdot {\vec {V}}={\vec {P}}:{\vec {\nabla }}{\vec {V}}}$,

on obtient l'équation suivante sur l'énergie interne par unité de masse :

${\displaystyle \rho \left({\dfrac {\partial e}{\partial t}}+{\vec {V}}\cdot {\vec {\nabla }}e\right)={\mathsf {P}}:{\vec {\nabla }}{\vec {V}}+{\vec {\nabla }}\cdot {\vec {q}}+{\vec {\nabla }}\cdot {\vec {q}}_{R}}$.

Formulation lagrangienne[modifier | modifier le code]

Dans certains problèmes le domaine occupé par le fluide peut varier considérablement au cours du temps. Il s'agit donc de problèmes instationnaires. C'est le cas dans les problèmes d'explosion ou en astrophysique. On fait alors appel aux variables lagrangiennes définies dans le repère noté ξ. L'accélération de la particule fluide est donnée par la dérivée particulaire :

${\displaystyle {\frac {\mathrm {D} \mathbf {\phi } }{\mathrm {D} t}}\,:=\left.{\frac {\partial \mathbf {\phi } }{\partial t}}\right|_{\xi }=\left.{\frac {\partial \mathbf {\phi } }{\partial t}}\right|_{x}+{\vec {V}}\cdot {\vec {\nabla }}\mathbf {\phi } }$.

Le dernier terme de cette équation est le terme d'advection de la quantité ϕ. Celle-ci peut être scalaire, vectorielle ou tensorielle.

Pour la quantité de mouvement, la dérivée particulaire vaut :

${\displaystyle {\begin{array}{rcl}{\dfrac {\mathrm {D} (\rho {\vec {V}})}{\mathrm {D} t}}=\left.{\dfrac {\partial (\rho {\vec {V}})}{\partial t}}\right|_{\xi }&=&\left.{\dfrac {\partial (\rho {\vec {V}})}{\partial t}}\right|_{x}+\left({\vec {V}}\cdot {\vec {\nabla }}\right)(\rho {\vec {V}})\\[0.8em]&=&\left.{\dfrac {\partial (\rho {\vec {V}})}{\partial t}}\right|_{x}+{\vec {\nabla }}\cdot \left(\rho {\vec {V}}{\vec {V}}\right)-\rho \left({\vec {\nabla }}\cdot {\vec {V}}\right){\vec {V}}\end{array}}}$.

Les équations de conservation dans le système de coordonnées définies par ${\displaystyle {\frac {\partial {\vec {x}}}{\partial t}}={\vec {V}}}$ s'écrivent :

• Équation de continuité (ou équation de bilan de la masse)

  ${\displaystyle {\frac {\mathrm {D} \rho }{\mathrm {D} t}}+\rho {\vec {\nabla }}\cdot {\vec {V}}=0}$

• Équation de bilan de la quantité de mouvement

  ${\displaystyle \rho {\frac {\mathrm {D} {\vec {V}}}{\mathrm {D} t}}=-{\vec {\nabla }}p+{\vec {\nabla }}\cdot {\mathsf {\Sigma }}+\rho {\vec {g}}}$

• Équation de bilan de l'énergie

  ${\displaystyle \rho {\frac {\mathrm {D} E}{\mathrm {D} t}}=-{\vec {\nabla }}\cdot \left(p{\vec {V}}\right)+{\vec {\nabla }}\cdot \left({\mathsf {\Sigma }}\cdot {\vec {V}}\right)+\rho {\vec {g}}\cdot {\vec {V}}+{\vec {\nabla }}\cdot {\vec {q}}+{\vec {\nabla }}\cdot {\vec {q}}_{R}}$

Expressions dans des systèmes de coordonnées[modifier | modifier le code]

En utilisant l'expression des opérateurs dans les divers systèmes courants de coordonnées il est possible de détailler les expressions des équations.

Repère en translation et rotation[modifier | modifier le code]

Il est parfois utile de décrire la dynamique des fluides dans un repère non galiléen, par exemple en physique de l'atmosphère ou pour décrire le mouvement d'un fluide dans un réservoir mobile, par exemple dans un lanceur.

On considère un repère orthonormé se déplaçant à la vitesse ${\displaystyle \textstyle {\vec {U}}(t)}$ par rapport au repère fixe et ayant une vitesse de rotation ${\displaystyle \textstyle {\vec {\Omega }}(t)}$ dans celui-ci.

Pour un point situé en ${\displaystyle \textstyle {\vec {r}}}$ dans le repère mobile, la formule de Varignon s'écrit :

${\displaystyle {\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}={\frac {\partial {\vec {r}}}{\partial t}}+{\vec {\Omega }}\wedge {\vec {r}}}$

Par dérivation, on obtient l'accélération apparente dans le repère mobile :

${\displaystyle {\vec {\Gamma }}={\frac {\mathrm {d} ^{2}{\vec {r}}}{\mathrm {d} t^{2}}}=2{\vec {\Omega }}\wedge {\vec {V}}+{\vec {\Omega }}\wedge \left({\vec {\Omega }}\wedge {\vec {r}}\right)+{\frac {\partial ^{2}{\vec {r}}}{\partial t^{2}}}+{\frac {\mathrm {d} \Omega }{\mathrm {d} t}}\wedge {\vec {r}}}$

Le premier terme dans le crochet est l'accélération de Coriolis et le deuxième est le terme centripète. Le troisième correspond au déplacement du repère mobile :

${\displaystyle {\frac {\partial ^{2}{\vec {r}}}{\partial t^{2}}}={\frac {\partial {\vec {U}}}{\partial t}}}$

Il existe donc un terme ${\displaystyle \textstyle \rho {\vec {\Gamma }}}$ à ajouter au premier membre de l'équation de la quantité de mouvement. Ce terme est d'ordre cinétique : il ne correspond pas à une force réelle et n'influence donc pas l'équation de conservation de l'énergie.

Fluide newtonien, hypothèse de Stokes[modifier | modifier le code]

En première approximation, pour de nombreux fluides usuels comme l'eau et l'air, le tenseur des contraintes visqueuses est proportionnel à la partie symétrique du tenseur des taux de déformation (hypothèse du fluide newtonien).

${\displaystyle {\mathsf {\Sigma }}=\mu \left[\,{\vec {\nabla }}{\vec {V}}+({\vec {\nabla }}{\vec {V}}\,)^{T}\right]+\mu '({\vec {\nabla }}\cdot {\vec {V}}\,)\;{\mathsf {I}}}$

• μ désigne la viscosité dynamique du fluide (unité : Poiseuille (Pl) = Pa s = N m⁻² s.)
• μ' désigne la seconde viscosité (ou viscosité volumique, en anglais volume viscosity) du fluide (unité : Poiseuille (Pl) = Pa s = N m⁻² s).

Ces coefficients dépendent en général de la masse volumique et de la température thermodynamique, comme au paragraphe suivant.

Avec l'expression du tenseur des contraintes visqueuses, l'équation de quantité de mouvement prend la forme :

${\displaystyle \rho \left[{\frac {\partial {\vec {V}}}{\partial t}}+\left({\vec {V}}\cdot {\vec {\nabla }}\right){\vec {V}}\right]=-{\vec {\nabla }}p+{\vec {\nabla }}\cdot \left\{\mu \left[{\vec {\nabla }}{\vec {V}}+({\vec {\nabla }}{\vec {V}}\,)^{T}\right]+\mu '({\vec {\nabla }}\cdot {\vec {V}})\,{\mathsf {I}}\,\right\}+\rho \,{\vec {g}}}$.

En supposant que les variations spatiales de ${\displaystyle \mu }$ et ${\displaystyle \mu '}$ sont négligeables, on obtient

${\displaystyle {\vec {\nabla }}\cdot {\mathsf {\Sigma }}=\mu \,\nabla ^{2}{\vec {V}}+(\mu +\mu ')\,{\vec {\nabla }}({\vec {\nabla }}\cdot {\vec {V}})}$,

dont on déduit

${\displaystyle \rho \left[{\frac {\partial {\vec {V}}}{\partial t}}+\left({\vec {V}}\cdot {\vec {\nabla }}\right){\vec {V}}\right]=-{\vec {\nabla }}p+\mu \,\nabla ^{2}{\vec {V}}+(\mu +\mu ')\,{\vec {\nabla }}({\vec {\nabla }}\cdot {\vec {V}})+\rho \,{\vec {g}}}$

On utilise généralement l'hypothèse de Stokes pour relier la viscosité dynamique à la seconde viscosité :

${\displaystyle \mu '+{\frac {2}{3}}\mu =0}$.

L'hypothèse de Stokes est vraie pour les gaz monoatomiques. Elle constitue une bonne approximation pour des fluides simples comme l'eau et l'air^[9].

A contrario, de nombreux fluides complexes, tels que les polymères, les hydrocarbures lourds, le miel, ou encore la pâte de dentifrice, ne vérifient pas l'hypothèse du fluide newtonien. On recourt alors à d'autres lois de comportement visqueux, dites non newtoniennes (par exemple la loi du fluide de Bingham). La science qui étudie les relations entre contrainte et déformation pour de tels fluides est la rhéologie.

Propriétés thermodynamiques[modifier | modifier le code]

Le système décrit ci-dessus est incomplet puisqu'il comporte 3 équations (dont une vectorielle) pour 5 inconnues (dont deux vectorielles) : ${\displaystyle \rho ,\,{\vec {V}},\,e,\,p,\,{\vec {q}}}$ (si l'on néglige le flux de chaleur dû au rayonnement, ${\displaystyle {\vec {q}}_{R}}$). On ajoute pour fermer le système des équations d'état de la forme

${\displaystyle p=p(\rho ,T),\quad e=e(\rho ,T),}$

où T représente la température thermodynamique ; par exemple la loi des gaz parfaits :

${\displaystyle p=\rho {\frac {R}{M}}T}$

où R désigne la constante des gaz parfaits et M la masse molaire du fluide.

Le système est alors fermé si l'on suppose vérifiée la loi de Fourier :

${\displaystyle {\vec {q}}=-\lambda \,{\vec {\nabla }}T}$

où λ désigne la conductivité thermique.

Propriétés de transport[modifier | modifier le code]

Gaz[modifier | modifier le code]

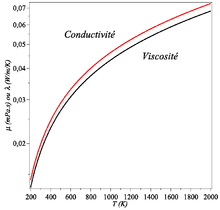
Les propriétés de transport, viscosité et conductivité, résultent d'une distribution hors d'équilibre thermodynamique dans le milieu (ne satisfaisant pas la statistique de Maxwell-Boltzmann). On sait les exprimer en utilisant la méthode de Chapman-Enskog^[9].

La viscosité s'exprime sous la forme suivante :

${\displaystyle \mu =\alpha {\frac {\sqrt {MT}}{f(T)}}}$

où f (T) est une fonction lentement variable avec T, découlant du potentiel d'interaction moléculaire. La viscosité d'un gaz varie donc approximativement comme √T. Elle est indépendante de la pression.

La conductivité est étroitement liée à la viscosité :

${\displaystyle {\frac {\lambda }{\mu }}=\left\{{\begin{array}{lcr}{\frac {5}{2}}C_{\mathcal {V}}\\[0.5em]C_{\mathcal {V}}+{\frac {15-6\chi }{4}}R\end{array}}\right.}$	pour un gaz monoatomique
	pour un gaz polyatomique

où ${\displaystyle C_{\mathcal {V}}=\left.{\frac {\partial e}{\partial T}}\right|_{\mathcal {V}}}$ est la capacité thermique massique à volume constant.

Dans cette expression χ = 1 correspond à la corrélation d'Eucken. La valeur exacte est plus proche de 1,3 en moyenne. Des calculs d'échanges au cours des collisions moléculaires permettent de préciser cette valeur, dépendante du gaz considéré et faiblement de la température.

Un mélange de gaz parfaits peut être traité comme un gaz unique en utilisant une approximation analytique (par exemple la loi de Sutherland) ou numérique du résultat du calcul des propriétés de ce mélange, qu'il s'agisse de la viscosité ou de la conductivité^[10].

Liquides[modifier | modifier le code]

La connaissance théorique pour les liquides est beaucoup moins avancée que pour les gaz et les prédictions dans ce domaine qualitatives : la viscosité diminue avec la température^[9],[11]. La connaissance des valeurs repose sur les mesures.

La variation de la conductivité avec la température ne présente pas de tendance marquée^[12],[13].

Restrictions à des cas plus simples[modifier | modifier le code]

Fluides incompressibles homogènes à viscosité constante[modifier | modifier le code]

L'écoulement d'un fluide est dit incompressible et homogène lorsque l'on peut négliger ses variations de masse volumique. Cette hypothèse est vérifiée pour l'eau liquide à température fixe et les métaux en fusion. Elle est aussi vérifiée pour les gaz lorsque le nombre de Mach ${\displaystyle {\mathcal {M}}a}$ est faible. En général, on considère l'écoulement incompressible lorsque ${\displaystyle {\mathcal {M}}a<0{,}3}$. De plus ce type de problème se rencontre dans des situations où la variation de température dans le milieu est faible et où l'on peut donc considérer la viscosité constante. Ceci est particulièrement vrai dans des liquides comme l'eau (voir courbe ci-dessus). De ce fait l'équation de l'énergie est découplée des équations de continuité et de quantité de mouvement, c'est-à-dire qu'on peut déterminer la vitesse et la pression indépendamment de l'équation de l'énergie. L'expression des équations de continuité et de quantité de mouvement sont considérablement simplifiées. On obtient alors

• Équation d'incompressibilité (se confondant avec l'équation de bilan de la masse pour un fluide homogène) :

${\displaystyle {\vec {\nabla }}\cdot {\vec {V}}=0}$.

• Équation de bilan de la quantité de mouvement :

${\displaystyle {\frac {\partial {\vec {V}}}{\partial t}}+({\vec {V}}\cdot {\vec {\nabla }})\,{\vec {V}}=-{\frac {1}{\rho }}{\vec {\nabla }}p+\nu \,\nabla ^{2}{\vec {V}}+{\vec {g}}}$

où ν = μ/ρ désigne la viscosité cinématique du fluide (unité SI : m² s⁻¹).

Le membre de gauche reflète l’accélération des particules du fluide.

Cette forme plus simple des équations de Navier-Stokes pour un milieu incompressible permet d'obtenir des solutions analytiques dans quelques cas :

• dans un tube cylindrique avec une différence de pression entre l'entrée et la sortie (écoulement de Poiseuille) ;
• dans un milieu semi-infini limité par un plan se déplaçant parallèlement à lui-même (problème de Rayleigh) ;
• entre deux plans dont l'un est en mouvement permanent par rapport à l'autre (écoulement de Couette) ;
• le jet de Landau-Squire, un exemple d'écoulement auto-similaire ;
• les écoulements potentiels en point d'arrêt comme l'écoulement de Hiemenz ;
• le tourbillon de Taylor-Green utilisé pour les benchmarks de méthodes de résolution numérique ;
• le tourbillon de Lamb-Oseen.

Il existe quelques autres exemples de solutions analytiques^{[14],[15],[16],[17]}.

En utilisant l'expression des opérateurs dans les divers systèmes courants de coordonnées il est possible de détailler les expressions.

Sous certaines hypothèses, on peut simplifier ces équations :

• en négligeant le terme inertiel ${\displaystyle {\vec {\nabla }}\cdot \left({\vec {V}}{\vec {V}}\right)}$ du cas général (qui est égal à ${\displaystyle ({\vec {V}}\cdot {\vec {\nabla }})\,{\vec {V}}}$ dans le cas incompressible), ce qui conduit à l'équation de Stokes,
• en utilisant une approximation de ce terme, ce qui conduit aux équations de Stokes-Oseen.

D’autre part, une expression de la pression peut être obtenue en prenant la divergence de l'équation de quantité de mouvement et en tenant compte de la relation d'incompressibilité :

${\displaystyle {\vec {\nabla }}^{2}p=-\rho \,{\vec {\nabla }}\cdot [{\vec {\nabla }}\cdot ({\vec {V}}{\vec {V}})]+\rho \,{\vec {\nabla }}\cdot {\vec {g}}}$.

Écoulements irrotationnels[modifier | modifier le code]

On définit le vecteur tourbillon (ou la vorticité) par :

${\displaystyle {\vec {\Omega }}={\vec {\nabla }}\times {\vec {V}}}$

où ${\displaystyle {\vec {\nabla }}\times {\vec {V}}}$ désigne le rotationnel de la vitesse.

On peut établir une équation de conservation pour cette quantité qui est l'équation de Helmholtz.

En partant de l'équation de quantité de mouvement du chapitre précédent avec l’hypothèse de Stokes, les identités vectorielles

${\displaystyle {\begin{array}{rcl}({\vec {V}}\cdot {\vec {\nabla }}){\vec {V}}&=&({\vec {\nabla }}\times {\vec {V}})\times {\vec {V}}+{\vec {\nabla }}V\,{\vec {V}}\\[0.5em]{\vec {\nabla }}\times ({\vec {\nabla }}\times {\vec {V}})&=&{\vec {\nabla }}({\vec {\nabla }}\cdot {\vec {V}})-\nabla ^{2}{\vec {V}}\end{array}}}$

permettent d’obtenir la forme suivante :

${\displaystyle \rho \left({\frac {\partial {\vec {V}}}{\partial t}}+{\vec {\Omega }}\times {\vec {V}}+{\vec {\nabla }}V\,{\vec {V}}\right)=-{\vec {\nabla }}p+\rho \,{\vec {g}}+\mu \left({\frac {4}{3}}\,{\vec {\nabla }}({\vec {\nabla }}\cdot {\vec {V}})-{\vec {\nabla }}\times {\vec {\Omega }}\right)}$.

Supposons que le vecteur tourbillon est nul. Dans ce cas^[b] :

${\displaystyle \rho \left({\frac {\partial {\vec {V}}}{\partial t}}+{\vec {\nabla }}V\,{\vec {V}}\right)=-{\vec {\nabla }}p+\rho \,{\vec {g}}+{\frac {4}{3}}\,\mu \,{\vec {\nabla }}({\vec {\nabla }}\cdot {\vec {V}})}$.

Dans ce cas toujours, puisque la vitesse ${\displaystyle {\vec {V}}}$ est un champ irrotationnel, on peut déduire qu'elle dérive d'un potentiel que l'on note ψ :

${\displaystyle {\vec {V}}={\vec {\nabla }}\psi }$.

En particulier dans le cas incompressible, si on reporte cette expression dans l'équation d'incompressibilité, le potentiel obéit à l'équation de Laplace :

${\displaystyle \nabla ^{2}\psi =0}$.

Si, de plus, le fluide est homogène et que la force ${\displaystyle {\vec {g}}}$ dérive d'un potentiel, par exemple la gravité, alors la propriété d'irrotationalité est automatiquement propagée en temps grâce à l'équation vérifiée par la vitesse.

Ces écoulements potentiels concernent les écoulements à faibles vitesses et peu visqueux : une voile de bateau ou une aile de planeur par exemple.

Analyse dimensionnelle[modifier | modifier le code]

Équations adimensionnelles[modifier | modifier le code]

Les équations de Navier-Stokes font intervenir 9 quantités ${\displaystyle \rho ,\,{\vec {V}},\,p,\,e,\,T,\,\mu ,\,{\vec {g}},\,{\vec {q}}_{R}}$, et 4 dimensions : temps, espace, masse, température. Le théorème de Vaschy-Buckingham montre donc l'existence de 5 variables adimensionnelles permettant l'analyse du système. Ces variables sont par exemple les nombres de Mach, Reynolds, Prandtl, Froude et Goulard. Il existe d'autres variables comme les nombres de Knudsen, de Strouhal, de Péclet ou beaucoup d'autres, mais celles-ci ne sont pas indépendantes. Les nombres de Mach, Reynolds et Knudsen par exemple sont liés entre eux, de même que les nombres de Péclet, Prandtl et Reynolds. Pour écrire ces nombres il faut définir des quantités de référence qui sont caractéristiques du problème étudié. Définissons les variables suivantes servant de références :

• une longueur L^*, par exemple la taille du domaine ouvert dans un problème de milieu poreux ou de microfluidique ou le rayon de courbure de paroi en aérodynamique,
• une vitesse V^*, une masse volumique ρ^* et une température T^*, par exemple les valeurs en amont (condition aux limites), d'où on déduit une pression ${\displaystyle p^{*}=\rho ^{*}{\frac {R}{M}}T^{*}}$,
• une seconde vitesse a^* pour la propagation des ondes sonores, par exemple ${\displaystyle a^{*}={\sqrt {\gamma ^{*}{\frac {R}{M}}T^{*}}}}$ pour un gaz parfait,
• une énergie interne e^*, par exemple ${\displaystyle e^{*}={\frac {p^{*}}{(\gamma ^{*}-1)\rho ^{*}}}={\frac {{a^{*}}^{2}}{\gamma ^{*}(\gamma ^{*}-1)}}}$ pour un gaz parfait,
• une viscosité μ^* et une conductivité λ^* éventuellement liée à μ^* (voir propriétés de transport),
• une accélération g^*,
• un flux radiatif q_R^*.

On peut alors définir pour ce problème les variables réduites suivantes :

- espace	${\displaystyle {\vec {\tilde {x}}}={\frac {\vec {x}}{L^{*}}}}$			- temps	${\displaystyle {\tilde {t}}={\frac {V^{*}}{L^{*}}}\,t}$		- masse volumique	${\displaystyle {\tilde {\rho }}={\frac {\rho }{\rho ^{*}}}}$		- pression	${\displaystyle {\tilde {p}}={\frac {p}{\rho ^{*}{a^{*}}^{2}}}}$
- viscosité	${\displaystyle {\tilde {\mu }}={\frac {\mu }{\mu ^{*}}}}$			- énergie interne	${\displaystyle {\tilde {e}}={\frac {e}{e^{*}}}}$		- flux radiatif	${\displaystyle {\vec {\tilde {q}}}_{R}={\frac {{\vec {q}}_{R}}{q_{R}^{*}}}}$		- conductivité	${\displaystyle {\tilde {\lambda }}={\frac {\lambda }{\lambda ^{*}}}}$
- vitesse	${\displaystyle {\vec {\tilde {V}}}={\frac {\vec {V}}{V^{*}}}}$

et les variables adimensionnelles :

- le nombre de Mach	${\displaystyle {\mathcal {M}}a={\frac {V^{*}}{a^{*}}}}$
- le nombre de Reynolds	${\displaystyle {\mathcal {R}}e={\frac {\rho ^{*}V^{*}L^{*}}{\mu ^{*}}}}$
- le nombre de Prandtl	${\displaystyle {\mathcal {P}}r={\frac {\mu ^{*}C_{P}^{*}}{\lambda ^{*}}}}$
- le nombre de Froude	${\displaystyle {\mathcal {F}}r={\frac {{V^{*}}^{2}}{g^{*}L^{*}}}}$
- le nombre de Goulard	${\displaystyle {\mathcal {G}}={\frac {2q_{R}^{*}}{\rho ^{*}{V^{*}}^{3}}}}$

Le système d'équations en valeurs réduites s'écrit comme suit.

• Conservation de la masse :

${\displaystyle {\frac {\partial {\tilde {\rho }}}{\partial {\tilde {t}}}}+{\vec {\nabla }}_{\tilde {x}}\cdot ({\tilde {\rho }}\,{\vec {\tilde {V}}})=0}$

où ${\displaystyle {\vec {\nabla }}_{\tilde {x}}=L^{*}{\vec {\nabla }}}$ est l'opérateur nabla adimensionné utilisé dans le système de coordonnées transformé.

• Conservation de la quantité de mouvement :

${\displaystyle {\frac {\partial }{\partial {\tilde {t}}}}({\tilde {\rho }}{\vec {\tilde {V}}})+{\vec {\nabla }}_{\tilde {x}}\cdot ({\tilde {\rho }}\,{\vec {\tilde {V}}}{\vec {\tilde {V}}})=-{\frac {1}{\gamma ^{*}{\mathcal {M}}a^{2}}}{\vec {\nabla }}_{\tilde {x}}\,{\tilde {p}}+{\frac {1}{{\mathcal {R}}e}}{\vec {\nabla }}_{\tilde {x}}\cdot {\tilde {\mathsf {\Sigma }}}+{\frac {1}{{\mathcal {F}}r}}\,{\tilde {\rho }}\,{\vec {\tilde {g}}}}$