导数 - 维基百科，自由的百科全书

系列條目
微积分学
函数 极限论 微分学 积分 微积分基本定理 微积分发现权之争（英语：Leibniz–Newton calculus controversy）
基础概念（含极限论和级数论） 實數性質 函数 单调性 初等函数 數列 极限 实数的构造 1=0.999… 无穷 銜尾蛇 無窮小量 ε-δ語言 实无穷（英语：Actual infinity） 大O符号 最小上界 收敛数列 芝诺悖论 柯西序列 单调收敛定理 夹挤定理 波尔查诺-魏尔斯特拉斯定理 斯托尔兹-切萨罗定理 上极限和下极限 函數極限 渐近线 邻域 连续 連續函數 不连续点 狄利克雷函数 稠密集 一致连续 紧集 海涅-博雷尔定理 支撑集 欧几里得空间 点积 叉积 三重积 拉格朗日恒等式 等价范数 坐標系 凸集 巴拿赫不动点定理 级数 收敛级数 几何级数 调和级数 項測試 格兰迪级数 收敛半径 审敛法 柯西乘积 黎曼级数重排定理 函数项级数（英语：function series） 一致收斂 迪尼定理 數列與級數 連續 函數
一元微分 差分 均差 微分 微分的线性 导数 流数法 二阶导数 光滑函数 高阶微分 莱布尼兹记号（英语：Leibniz's_notation） 幽灵似的消失量 介值定理 中值定理 罗尔定理 拉格朗日中值定理 柯西中值定理 泰勒公式 求导法则 乘积法则 广义莱布尼茨定则（英语：General Leibniz rule） 除法定则 倒数定则 链式法则 洛必达法则 反函数的微分 Faà di Bruno公式（英语：Faà di Bruno's formula） 对数微分法 导数列表 导数的函数应用 单调性 切线 极值 驻点 拐点 求导检测（英语：derivative test） 凸函數 凹函數 簡森不等式 曲线的曲率 埃尔米特插值 达布定理 魏尔施特拉斯函数
一元积分 积分表 定义 不定积分 定积分 黎曼积分 达布积分 勒贝格积分 积分的线性 求积分的技巧 换元积分法 三角换元法 分部积分法 部分分式积分法 降次积分法 微元法 积分第一中值定理 积分第二中值定理 微积分基本定理 反常積分 柯西主值 積分函數 Β函数 Γ函数 古德曼函数 椭圆积分 數值積分 矩形法 梯形公式 辛普森積分法 牛顿-寇次公式 积分判别法 傅里叶级数 狄利克雷定理 周期延拓 魏尔施特拉斯逼近定理 帕塞瓦尔定理 刘维尔定理
多元微积分 偏导数 隐函数 全微分 微分的形式不变性 二阶导数的对称性 全微分 方向導數 标量场 向量場 梯度 Nabla算子 多元泰勒公式 拉格朗日乘数 黑塞矩陣 鞍點 多重积分 逐次积分 积分顺序（英语：Order of integration (calculus)） 积分估值定理 旋转体 帕普斯-古尔丁中心化旋转定理 祖暅-卡瓦列里原理 托里拆利小号 雅可比矩阵 广义多重积分 高斯积分 若尔当曲线 曲线积分 曲面积分 施瓦茨的靴（俄语：Сапог Шварца） 散度 旋度 通量 可定向性 格林公式 高斯散度定理 斯托克斯定理及其外微分形式 若尔当测度 隐函数定理 皮亚诺-希尔伯特曲线 积分变换 卷积定理 积分符号内取微分 莱布尼茨积分定则（英语：Leibniz integral rule） 多变量原函数的存在性 全微分方程 外微分的映射原像存在性 恰当形式 向量值函数 向量空间内的导数推广（英语：generalizations of the derivative） 加托导数 弗雷歇导数 矩阵的微积分（英语：matrix calculus） 弱微分
微分方程 常微分方程 柯西-利普希茨定理 皮亚诺存在性定理 分离变数法 级数展开法 积分因子 拉普拉斯算子 欧拉方法 柯西-欧拉方程 伯努利微分方程 克莱罗方程 全微分方程 线性微分方程 叠加原理 特徵方程式 朗斯基行列式 微分算子法 差分方程 拉普拉斯变换 偏微分方程 拉普拉斯方程 泊松方程 施图姆-刘维尔理论 N体问题 积分方程
相关数学家 牛顿 莱布尼兹 柯西 魏尔斯特拉斯 黎曼 拉格朗日 欧拉 帕斯卡 海涅 巴罗 波尔查诺 狄利克雷 格林 斯托克斯 若尔当 达布 傅里叶 拉普拉斯 雅各布·伯努利 約翰·白努利 阿达马 麦克劳林 迪尼 沃利斯 费马 达朗贝尔 黑维塞 吉布斯 奥斯特罗格拉德斯基 刘维尔 棣莫弗 格雷果里 玛达瓦（英语：Madhava of Sangamagrama） 婆什迦羅第二 阿涅西 阿基米德
历史名作 从无穷小量分析来理解曲线（英语：Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes） 分析学教程（英语：Cours d'Analyse） 无穷小分析引论 用无穷级数做数学分析（英语：De analysi per aequationes numero terminorum infinitas） 流形上的微积分（英语：Calculus on Manifolds (book)） 微积分学教程 纯数学教程（英语：A Course of Pure Mathematics） 机械原理方法论（英语：The Method of Mechanical Theorems）
分支学科 实变函数论 複分析 傅里叶分析 变分法 特殊函数 动力系统 微分几何 微分代数 向量分析 分数微积分 玛里亚温微积分（英语：Malliavin calculus） 随机分析 最优化 非标准分析
查 论 编

导数（英語：derivative）是微积分学中的一個概念。函数在某一点的导数是指这个函数在这一点附近的变化率（即函数在这一点的切线斜率）。导数的本质是通过极限的概念对函数进行局部的线性逼近。当函数${\displaystyle f}$的自变量在一点${\displaystyle x_{0}}$上产生一个增量${\displaystyle h}$时，函數输出值的增量與自變量增量${\displaystyle h}$的比值在${\displaystyle h}$趋于0时的極限如果存在，即為${\displaystyle f}$在${\displaystyle x_{0}}$处的导数，记作${\displaystyle f'(x_{0})}$、${\displaystyle {\frac {\mathrm {d} f}{\mathrm {d} x}}(x_{0})}$或${\displaystyle \left.{\frac {\mathrm {d} f}{\mathrm {d} x}}\right|_{x=x_{0}}}$。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度^[1]:155。

导数是函数的局部性质。不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导(可微分)，否则称为不可导(不可微分)。如果函数的自变量和取值都是实数的话，那么函数在某一点的导数就是该函数所代表的曲线在這一点上的切线斜率。

对于可导的函数${\displaystyle f}$，${\displaystyle x\mapsto f'(x)}$也是一个函数，称作${\displaystyle f}$的导函数。寻找已知的函数在某点的导数或其导函数的过程称为求导（英語：differentiation）。反之，已知导函数也可以倒过来求原来的函数，即不定积分。微积分基本定理说明了求原函数与积分是等价的^[1]:372。求导和积分是一对互逆的操作，它们都是微积分学中最为基础的概念。

直觀上 ${\displaystyle f(x)-f(a)}$代表函數值從 ${\displaystyle a}$ 到 ${\displaystyle x}$ 的變化量，那這樣，

代表的是從 ${\displaystyle a}$ 到 ${\displaystyle x}$ 的平均變化率，如果把 ${\displaystyle x}$ 趨近於 ${\displaystyle a}$，似乎就可以更能貼切的描述函數值在 ${\displaystyle a}$ 附近的變化。

以此為動機，若实函数 ${\displaystyle f}$ 於实数 ${\displaystyle a}$ 有定義，且以下極限（注意這個表達式所定義的函數定義域不含 ${\displaystyle a}$ ）

存在則称 ${\displaystyle f}$ 於 ${\displaystyle a}$ 处可导，并称这个极限为 ${\displaystyle f}$ 於 ${\displaystyle a}$ 处的导数^[2]:117-118，记为${\displaystyle f^{\prime }(a)}$也可记作 ${\displaystyle \left.{\frac {\mathrm {d} f}{\mathrm {d} x}}\right|_{x=a}}$ 或 ${\displaystyle {\frac {\mathrm {d} f}{\mathrm {d} x}}(a)}$ ^[1]:154。

根據函數極限的定義，導數定義部分的 ＂存在 ${\displaystyle \delta >0}$ 使所有的 ${\displaystyle x\in D_{f}}$ ，只要 ${\displaystyle 0<|x-a|<\delta }$ 都有....＂ 可以直觀的理解為 ＂當 ${\displaystyle h=x-a}$ 趨近於 ${\displaystyle 0}$ 都有....＂，但要把它寫成嚴謹的定義，會碰到 ＂存在 ${\displaystyle \delta >0}$ 對所有的實數 ${\displaystyle h}$ ，只要 ${\displaystyle a+h\in D_{f}}$ 且 ${\displaystyle 0<|h|<\delta }$ 都有....＂這段敘述無法直接套入極限定義的問題，對此必須把以下的表達式

定義為導數原始極限表達式的簡記，而非另一種自動合法的導數定義。但如果存在 ${\displaystyle r>0}$ ，使 ${\displaystyle f}$ 在 ${\displaystyle (a-r,\,a+r)}$ 裡都有定義，那定義 ${\displaystyle F}$ 為以

為定義域，然後以

為對應規則的函數，那以下的極限式

就可以把以 ${\displaystyle h}$ 為自變數的偏差，將之趨近於零求導數的想法納入正式的運算裡。

当函数定义域和取值都在实数域中的时候，导数可以表示函数的曲线上的切线斜率。如右图所示，设${\displaystyle P_{0}}$为曲线上的一个定点，${\displaystyle P}$为曲线上的一个动点。当${\displaystyle P}$沿曲线逐渐趋向于点${\displaystyle P_{0}}$时，并且割线${\displaystyle PP_{0}}$的极限位置${\displaystyle P_{0}T}$存在，则称${\displaystyle P_{0}T}$为曲线在${\displaystyle P_{0}}$处的切线。

若曲线为一函数${\displaystyle y=f(x)}$的图像，那么割线${\displaystyle PP_{0}}$（粉紅色）的斜率为：

当${\displaystyle P_{0}}$处的切线${\displaystyle P_{0}T}$（橘紅色），即${\displaystyle PP_{0}}$的极限位置存在时，此时${\displaystyle \Delta x\to 0}$，${\displaystyle \varphi \to \alpha }$，则${\displaystyle P_{0}T}$的斜率${\displaystyle \tan \alpha }$为：

上式与一般定义中的导数定义完全相同，也就是说${\displaystyle f'(x_{0})=\tan \alpha }$，因此，导数的几何意义即曲线${\displaystyle y=f(x)}$在点${\displaystyle P_{0}(x_{0},f(x_{0}))}$处切线的斜率。^{[2]:117[1]:153}

若函数 ${\displaystyle \;f(x)\;}$ 在其定义域包含的某区间 ${\displaystyle \;I\;}$ 内每一个点都可导，那么也可以说函数${\displaystyle \;f(x)\;}$ 在区间 ${\displaystyle \;I\;}$ 内可导，这时对于 ${\displaystyle \;I\;}$ 内每一个确定的${\displaystyle \;x\;}$ 值，都对应着 ${\displaystyle \;f\;}$ 的一个确定的导数值，如此一来就构成了一个新的函数${\displaystyle x\mapsto f'(x)}$，这个函数称作原来函数 ${\displaystyle \;f(x)\;}$ 的导函数^[1]:155，记作：${\displaystyle \;y'\;}$、${\displaystyle f'(x)\;}$ 或者 ${\displaystyle {\tfrac {\mathrm {d} f}{\mathrm {d} x}}(x)}$。值得注意的是，导数是一个数，是指函数 ${\displaystyle f(x)\;}$ 在点 ${\displaystyle x_{0}\;}$ 处导函数的函数值。但在不至于混淆的情况下，通常也可以说导函数为导数。

由于对每一个可导的函数 ${\displaystyle \;f(x)\;}$，都有它的导函数 ${\displaystyle f'(x)\;}$ 存在，我们还可以定义将函数映射到其导函数的算子。这个算子称为微分算子，一般记作 ${\displaystyle D}$ 或 ${\displaystyle {\tfrac {\mathrm {d} }{\mathrm {d} x}}}$^[3]。例如：

${\displaystyle {\begin{aligned}D(x\mapsto 1)&=(x\mapsto 0)\\D(x\mapsto x)&=(x\mapsto 1)\\D(x\mapsto x^{2})&=(x\mapsto 2\cdot x)\end{aligned}}}$

由于微分算子的输出值仍然是函数，可以继续求出它在某一点的取值。比如说对于函数 ${\displaystyle \;f(x)=x^{2}\;}$，

${\displaystyle D(f)=(x\mapsto 2\cdot x)}$

所以${\displaystyle D(f)(x)=2x}$，${\displaystyle D(f)(1.4)=2\times 1.4=2.8}$。

微分也是一种线性描述函数在一点附近变化的方式。微分和导数是两个不同的概念。但是，对一元函数来说，可微与可导是完全等价的。可微的函数，其微分等于导数乘以自变量的微分${\displaystyle \mathrm {d} x}$，换句话说，函数的微分与自变量的微分之商等于该函数的导数。因此，导数也叫做微商。函数${\displaystyle y=f(x)}$的微分又可记作${\displaystyle \mathrm {d} y=f'(x)\mathrm {d} x}$^[4]。

导数和积分的发现是微积分发明的关键一步。17世纪以来，光学透镜的设计以及炮弹弹道轨迹的计算促使欧洲的数学家对曲线的切线进行研究。1630年代，法国数学家吉尔·德·罗伯瓦尔作出了最初的尝试^[5]。与此同时，同是法国人的费马在计算切线时已经使用了无穷小量的概念^{[註 1][6]:52}。

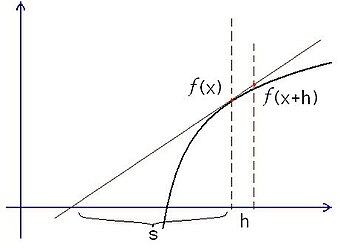
如右图，费马考虑曲线 ${\displaystyle f(x)}$ 在 ${\displaystyle x}$ 处的切线。他声称，对于切线，有以下的关系成立：

${\displaystyle {\frac {s}{s+h}}={\frac {f(x)}{f(x+h)}}}$

对上式变形后得到：

${\displaystyle s={\frac {f(x)}{\frac {f(x+h)-f(x)}{h}}}}$

对于具体的函数 ${\displaystyle f(x)}$，比如 ${\displaystyle f(x)=x^{3}}$，费马计算 ${\displaystyle {\frac {f(x+h)-f(x)}{h}}}$ 的值，并将 ${\displaystyle h}$设为0，就得到 ${\displaystyle s}$，从而确定切线的斜率。可以看出，费马的方法实质上已经是求导。费马还给出了 ${\displaystyle f(x)}$ 为多项式时切线的公式。英国的巴罗、荷兰的于德（Johnann Van Waveren Hudde）和瓦隆的斯卢兹（René Francoiss Walther de Sluze）继续了费马的工作^[7]。然而，费马和巴罗等人并没有将求导归纳为一种独立的工具，只是给出了具体的计算技巧^[5]。

1660年代，英国人伊萨克·牛顿提出了“流数”的概念。牛顿在写于1671年的《流数法与无穷级数》中对流数的解释是：“我把时间看作是连续的流动或增长，而其他的量则随着时间而连续增长。我从时间流动性出发，把所有其他量的增长速度称为流数。”也就是说，流数就是导数。牛顿将无穷小的时间间隔定义为“瞬间”（moment），而一个量的增量则是流数与瞬间的乘积。求导数时，牛顿将自变量和因变量两边展开，同时除以瞬间，再将剩下的项中含有瞬间的项忽略掉^[6]:72。而在他的第三篇微积分论文中，牛顿使用了新的概念：最初比和最后比。他说：

“

随我们的意愿，流数可以任意地接近于在尽可能小的等间隔时段中产生的增量，精确地说，它们是最初增量的最初的比，它们也能用和它们成比例的任何线段来表示。[6]:74

”

相比于牛顿，德国数学家莱布尼兹使用了更清晰的记号来描述导数（见导数的记法一节）。他利用了巴罗的“微分三角形”概念，将自变量和因变量的增量记为 ${\displaystyle dx}$ 和 ${\displaystyle dy}$。他把 ${\displaystyle dx}$ 理解为“比任何给定的长度都要小”，而 ${\displaystyle dy}$ 则是 ${\displaystyle x}$ 移动时 ${\displaystyle y}$“瞬刻的增长”^[6]:89。而导数则是两者之间的比例。他还研究了函数之和、差、积、商的求导法则。

牛顿和莱布尼兹的差别在于，牛顿将无穷小量作为求流数或导数的工具，而莱布尼兹则用无穷小量的比值来表示导数。这与二人的哲学思想差异有关^[6]:92。

微积分的理论面世后，遭到了有关无穷小量定义的攻击与质疑。导数的定义自然也包括在内。莱布尼兹和牛顿对无穷小量的认识都是模糊的。不仅如此，莱布尼兹甚至引入了${\displaystyle (d)x}$ 和 ${\displaystyle (d)y}$，称其为“未消失的量”，用以进行求导前部的计算。在完成计算后再用“消失的量”${\displaystyle dx}$ 和 ${\displaystyle dy}$来代替它们，并假定前两者之比等于后两者之比，认为这是一个不容置疑的真理^[6]:102。

许多数学家，包括伯努利兄弟、泰勒、麦克劳林、达朗贝尔、拉格朗日和欧拉都想要对微积分的严密性辩护或将微积分严密化。但受限于对无穷小量的认识，十八世纪的数学家并没有做出太大的成果。微积分的强烈抨击者，英国的乔治·贝克莱主教在攻击无穷小量时认为，流数实际上是“消失的量的鬼魂”，是0与0之比。欧拉承认后者，并认为0与0之比可以是有限值。拉格朗日则假定函数都可以展开为幂级数，并在此基础上定义导数^[6]:154-156。

十九世纪后，随着对函数连续性和极限的更深刻认识，微积分终于趋于严谨。波尔查诺是首先将导数定义为函数值的改变量与自变量增量之比在自变量增量无限接近0时趋向的量。波尔查诺强调导数不是0与0之比，而是前面的比值趋向的数^[8]:10。柯西在他的著作《无穷小分析教程概论》中也使用了同样的定义，并定义${\displaystyle dy}$ 为导数与 ${\displaystyle dx}$ 的乘积。这样，导数和微分的概念得到了统一^[8]:11。

从微积分发轫至如今，不同的数学家都曾使用过不同的记号来表示函数的导数。部分记号至今仍然使用，成为现代的通用记法。

作为微积分的发明人之一，牛顿在1704年著作中将导数用函数符号上方的点来表示。例如 ${\displaystyle y=f(x)}$的导数就记作${\displaystyle {\dot {y}}}$，而二阶导数则记为${\displaystyle {\ddot {y}}}$^[9]:193-196。他以后的数学家也会将${\displaystyle {\dot {y}}}$用来表示函数的微分。牛顿的记法中没有明确自变量，因此 ${\displaystyle y}$ 对 ${\displaystyle x}$ 的导数在牛顿的著作中也会被记成${\displaystyle y':x'}$，因为这可以理解为两个函数${\displaystyle y}$ 和 ${\displaystyle x}$ 对于另一个变量${\displaystyle t}$ 的导数比^[9]:196。而这个导数比（使用莱布尼兹的记号）：

${\displaystyle y':x'={\frac {dy}{dt}}:{\frac {dx}{dt}}={\frac {dy}{dx}}}$

牛顿的记号多见于物理学或与之有关的方面，如微分方程中。以及直到现在，使用函数符号上加一点来表示某一变量的变化率（即对时间的导数）依然常见于各类物理学教材中（如使用${\displaystyle {\dot {v}}}$来表示加速度等）。注意到对于高阶的导数，这种记法就无法表示了。

莱布尼兹在他的研究中分别使用 ${\displaystyle \Delta x}$ 和 ${\displaystyle \Delta y}$ 来表示函数自变量和應变量（输出值）的有限变化量，而使用 ${\displaystyle dx}$ 和 ${\displaystyle dy}$ 来表示“无限小”的变化量（即所谓的“无穷小量”）^[10]。如果将函数记为${\displaystyle y=f(x)}$的话，那么在莱布尼兹的记法下，其导数记为：

${\displaystyle {\frac {dy}{dx}}}$、${\displaystyle {\frac {df}{dx}}(x)}$、${\displaystyle {\frac {d}{dx}}f(x)}$ 或 ${\displaystyle {\frac {d\left(f(x)\right)}{dx}},}$

这个记法最早出现在莱布尼兹1684年的论文中^[9]:204，莱布尼兹在之前的文章中会将 ${\displaystyle dx}$ 记成 ${\displaystyle {\tfrac {x}{d}}}$，把 ${\displaystyle {\tfrac {dy}{dx}}}$ 记成 ${\displaystyle d{\tfrac {y}{x}}}$。莱布尼兹记法的好处是明确了自变量和應变量^[11]。要注意的是记号${\displaystyle dx}$是一个整体，${\displaystyle dy}$也是，而${\displaystyle {\frac {dy}{dx}}}$可以看成一个整体，也可以不严谨地看成${\displaystyle dy}$和${\displaystyle dx}$的比值^[10]。此外，${\displaystyle {\frac {dy}{dx}}}$ 表示的是导函数，在某一点 ${\displaystyle x=a}$ 的导数则记为：${\displaystyle \left.{\frac {dy}{dx}}\right|_{x=a}}$ 对于更高阶的导数（比如说n阶，见高阶导数一节），莱布尼兹的记法是：

${\displaystyle {\frac {d^{n}y}{dx^{n}}}}$、${\displaystyle {\frac {d^{n}f}{dx^{n}}}(x)}$ 或 ${\displaystyle {\frac {d^{n}\left[f(x)\right]}{dx^{n}}},}$

这种记法是在1695年出现的^[9]:205。这里的分子和分母不再具有单独的意义。莱布尼兹的记法中使用 ${\displaystyle {\frac {d}{dx}}}$ 来表示微分算子，比如说二阶的导数 ${\displaystyle {\frac {d^{2}y}{dx^{2}}}}$ 就可以看成：

${\displaystyle {\frac {d^{2}y}{dx^{2}}}={\frac {d}{dx}}\left({\frac {dy}{dx}}\right)}$^[11]

莱布尼兹记法的另一个好处是便于记忆导数计算的法则。例如链式法则（见导数的计算一节）应用莱布尼兹的记法就是：

${\displaystyle {\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}}$

可以想象为右边是两个分式的乘积，消去${\displaystyle du}$之后就变成左边^[11]。

由于牛顿和莱布尼兹之间关于微积分创始人称号的持久纠纷，在十八世纪早期的很长时间里，英国数学界与欧洲大陆的数学界分别采用牛顿和莱布尼兹的记号，泾渭分明。这种情况直到十八世纪后期才开始改变，随着拉格朗日记法的出现而变得多样化起来^[9]:197-200。

另一种现今常见的记法是十八世纪拉格朗日于1797年率先使用的，以在函数的右上角加上一短撇作为导数的记号。函数 ${\displaystyle y=f(x)}$ 的导数就记作 ${\displaystyle f'(x)}$ 或 ${\displaystyle y'}$^[12]。二阶和三阶导数记为${\displaystyle f''(x)}$、${\displaystyle y''}$ 和 ${\displaystyle f'''(x)}$、${\displaystyle y'''}$^[9]:207。如果需要处理更高阶的导数，则用括号内的求导阶数n来代替短撇，记为：${\displaystyle f^{(n)}(x)}$、${\displaystyle y^{(n)}}$。当十九世纪的数学家柯西处理微分学时，他认为莱布尼兹的记法“模糊不便”，而采用更为“紧凑”的记法，将 ${\displaystyle {\frac {dy}{dx}}}$ 记为${\displaystyle y'_{x}}$。这种记法可说是拉格朗日记法的变种^[9]:218。后来这种记法曾继续被精简为${\displaystyle y_{x}}$^[13]。

十九世纪以前，尽管大部分数学家会选择采用牛顿、莱布尼兹或拉格朗日的记号来表示导数，但也有很多的数学家希望使用自己的方法来记录。在不同数学家的著作中可以看到各种主流记法的混合或变体。数学家之间关于什么样的记法最为简便和严谨也是各执一词。同时，由于函数的微分、导数、偏导数以及无穷小量等概念尚未成熟，记号的不统一更增加了数学家之间相互理解的难度^[9]:214-234。十九世纪初期的德国数学家马尔丹·欧姆采用${\displaystyle \partial f(x)}$来表示导数，而同时期的雅可比则采用${\displaystyle {\frac {\partial f}{\partial x}}}$来表示偏导数。同时许多数学家采用${\displaystyle {\frac {df}{dx}}}$^[14]、${\displaystyle {\frac {d}{x}}f}$^[15]或 ${\displaystyle {\frac {\delta f}{\delta x}}}$^[16]表示偏导数。

用大写字母${\displaystyle D}$表示导数从十八世纪末就开始。1800年，法国数学家路易斯·弗朗索瓦·安托内·阿伯加斯特（Louis François Antoine Arbogast）使用${\displaystyle D^{m}f}$表示函数 ${\displaystyle f}$ 的m阶导数或全微分^[17]。而其后本杰明·佩尔斯也使用${\displaystyle Df\cdot x}$表示 ${\displaystyle f}$ 对 ${\displaystyle x}$ 的导数^[18]。而柯西也采用类似的记号，用${\displaystyle D_{x}^{m}f}$表示函数 ${\displaystyle f}$ 对 ${\displaystyle x}$ 的m阶偏导数^[19]。

如果一个函数的定义域为全体实数，即函数在${\displaystyle (-\infty ,+\infty )}$上都有定义，那么该函数是不是在定义域上处处可导呢？答案是否定的。函数在定义域中一点可导需要一定的条件。首先，要使函数${\displaystyle f}$在一点可导，那么函数一定要在这一点处连续。换言之，函数若在某点可导，则必然在该点处连续。这个结论来自于连续性的定义。

符号函数（sgn函数）是一个不连续的函数在断点处不可导的例子：

首先注意到这个函数在${\displaystyle x_{0}=0}$处不连续。作为验证，可以求出函数在${\displaystyle x=0}$处附近的变化率，根据函数可导的条件再进行判断：

该函数在${\displaystyle x_{0}=0}$左侧附近的变化率为：${\displaystyle {\frac {f(x)-f(x_{0})}{x-x_{0}}}={\frac {-1-0}{x-0}}=-{\frac {1}{x}}}$

当${\displaystyle x\to 0^{-}}$时，上面的比值趋于正无穷大发散，不存在，故这个符号函数在${\displaystyle x_{0}=0}$处不可导。

然而，连续性并不能保证可导性。即使函数在一点上连续，也不一定就在这一点可导。事实上，存在着在每一点都连续，但又在每一点都不可导的“病态函数”。1931年，斯特凡·巴拿赫甚至证明，事实上“绝大多数”的连续函数都属于这种病态函数（至少在一点可导的连续函数在所有连续函数中是贫集）^[20]。在连续而不可导的函数里，一种常见的情况是，函数在某一点连续，并且可以定义它的左导数和右导数：

然而左导数和右导数并不相等，因而函数在该处不可导。实际上，若函数导数存在，则必然可以推出左右导数相等，这是由极限的性质（极限存在则左右极限相等）得来：

下面以绝对值函数作为例子：

该函数在${\displaystyle x=0}$处的左导数为：${\displaystyle f'_{-}(0)=\lim _{x\to 0^{-}}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\to 0^{-}}{\frac {-x-0}{x-0}}=-1}$

该函数在${\displaystyle x=0}$处的右导数为：${\displaystyle f'_{+}(0)=\lim _{x\to 0^{+}}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\to 0^{+}}{\frac {x-0}{x-0}}=1}$

绝对值函数在${\displaystyle x=0}$处的左右导数皆存在，但由于左右导数不相等，故绝对值函数在${\displaystyle x=0}$处不可导。^[2]:118-119

如果函数在一点的左右导数都存在并且相等，那么函数在该处可导。^[1]:155

通过认识可导函数的导数，可以推断出不少函数本身的性质。

根据微积分基本定理，对于可导的函数${\displaystyle f}$，有：

${\displaystyle f(b)-f(a)=\int _{a}^{b}f'(t)\mathrm {d} t}$

如果函数的导函数在某一区间内恒大于零（或恒小于零），那么函数在这一区间内单调递增（或单调递减），这种区间也称为函数的单调区间。导函数等于零的点称为函数的驻点（或极值可疑点），在这类点上函数可能会取得极大值或极小值。进一步判断则需要知道导函数在附近的符号。对于满足 ${\displaystyle f'(x_{0})=0}$ 的一点 ${\displaystyle x_{0}}$，如果存在 ${\displaystyle \delta >0}$ 使得 ${\displaystyle f'}$ 在区间${\displaystyle (x_{0}-\delta ,x_{0}]}$ 上都大于等于零，而在区间 ${\displaystyle [x_{0},x_{0}+\delta )}$ 上都小于等于零，那么 ${\displaystyle x_{0}}$ 是一个极大值点，反之则为极小值点^[2]:170。如果${\displaystyle f''(x_{0})=0}$ 並且 ${\displaystyle f''(x)}$ 在 ${\displaystyle x_{0}}$ 改變加減號，則称这个点是拐点；否則这个点不是拐点。^[21]:200

如果函数在 ${\displaystyle x_{0}}$ 处的二阶导数 ${\displaystyle f''(x_{0})}$ 存在，极值点也可以用它的正负性判断（已确定${\displaystyle f'(x_{0})=0}$）。如果${\displaystyle f''(x_{0})>0}$，那么 ${\displaystyle x_{0}}$ 是一个极小值点，反之为极大值点^[2]:170-171。

可导函数的凹凸性与其导数的单调性有关。如果函数的导函数在某个区间上单调递增，那么这个区间上函数是向下凸的，反之则是向上凸的。如果二阶导函数存在，也可以用它的正负性判断，如果在某个区间上 ${\displaystyle f''}$ 恒大于零，则这个区间上函数是向下凸的，反之这个区间上函数是向上凸的^[2]:176-178。

原则上，函数的导数可以通过考虑差商和计算其极限来从定义计算。在实践中，一旦知道了一些简单函数的导数，就可以使用从更简单的函数获得更复杂函数的导数的规则，来更容易地计算其他函数的导数。

所谓基本函数是指一些形式简单并且容易求出导数的函数。这些基本函数的导函数可以通过定义直接求出。

• 幂函数的导数：如果

${\displaystyle f(x)=x^{r},}$

其中${\displaystyle r}$是任意实数，那么

${\displaystyle f'(x)=rx^{r-1},}$函数${\displaystyle f}$的定义域可以是整个实数域，但导函数的定义域则不一定与之相同。例如当 ${\displaystyle r={\frac {1}{2}}}$时：

${\displaystyle f'(x)={\frac {1}{2}}x^{-{\tfrac {1}{2}}}\,}$^[2]:119

导函数的定义域只限所有正实数而不包括0。需要注意的是，不会有多项式函数的导数为${\displaystyle \scriptstyle x^{-1}}$。当 ${\displaystyle r=0}$ 时，常函数的导数是0。

• 底数为${\displaystyle e}$的指数函数 ${\displaystyle \scriptstyle y=e^{x}}$ 的导数还是自身：${\displaystyle \scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}.}$ 而一般的指数函数 ${\displaystyle y=a^{x}}$ 的导数还需要乘以一个系数：${\displaystyle \scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}a^{x}=\ln(a)a^{x}.}$^[2]:122

自然对数函数的导数则是 ${\displaystyle x^{-1}}$：${\displaystyle \scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}\ln(x)={\frac {1}{x}},\qquad x>0.}$^[2]:123 同样的，一般的对数函数导数则还需要乘以一个系数：${\displaystyle \scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}\log _{a}(x)={\frac {1}{x\ln(a)}}}$

• 三角函数的导数仍然是三角函数，或者由三角函数构成^[2]:122:

${\displaystyle {\frac {d}{dx}}\sin(x)=\cos(x).}$

${\displaystyle {\frac {d}{dx}}\cos(x)=-\sin(x).}$

${\displaystyle {\frac {d}{dx}}\tan(x)=\sec ^{2}(x)={\frac {1}{\cos ^{2}(x)}}=1+\tan ^{2}(x).}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\cot(x)=-\csc ^{2}(x)=-{\frac {1}{\sin ^{2}(x)}}.}$

• 反三角函数的导数则是无理分式^[1]:160:

${\displaystyle {\frac {d}{dx}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.}$

${\displaystyle {\frac {d}{dx}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.}$

${\displaystyle {\frac {d}{dx}}\arctan(x)={\frac {1}{1+x^{2}}}}$

由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。基本的求导法则如下：

• 求导的线性性：对函数的线性组合求导，等于先对其中每个部分求导后再取线性组合。

${\displaystyle (af+bg)'=af'+bg'\,}$ （其中${\displaystyle a,b}$为常数）^[2]:121

• 两个函数的乘积的导函数，等于其中一个的导函数乘以另一者，加上另一者的导函数与其的乘积

${\displaystyle (fg)'=f'g+fg'\,}$ ^[2]:125

• 两个函数的商的导函数也是一个分式。其中分子是分子函数的导函数乘以分母函数减去分母函数的导函数乘以分子函数后的差，而其分母是分母函数的平方。

${\displaystyle \left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}}$ （在${\displaystyle g(x)\neq 0}$处方有意义）^[2]:126

• 复合函数的求导法则：如果有复合函数 ${\displaystyle f(x)=h[g(x)]}$，那么

${\displaystyle f'(x)=h'[g(x)]\cdot g'(x).\,}$^[2]:128

若要求某个函数在某一点的导数，可以先运用以上方法求出这个函数的导函数，再看导函数在这一点的值。

欲求函数

${\displaystyle f(x)=x^{4}+\sin(x^{2})-\ln(x)e^{x}+7\,}$

在${\displaystyle x=3}$处的导数。可以先求出其导函数：

${\displaystyle {\begin{aligned}f'(x)&=4x^{(4-1)}+{\frac {\mathrm {d} \left(x^{2}\right)}{\mathrm {d} x}}\cos(x^{2})-\left[{\frac {\mathrm {d} \left(\ln {x}\right)}{\mathrm {d} x}}e^{x}+\ln {x}{\frac {\mathrm {d} \left(e^{x}\right)}{\mathrm {d} x}}\right]+0\\&=4x^{3}+2x\cos(x^{2})-{\frac {1}{x}}e^{x}-\ln(x)e^{x}.\end{aligned}}}$

其中第二项使用了复合函数的求导法则，而第三项则使用了乘积的求导法则。求出导函数后，再将${\displaystyle x=3}$代入，得到导数为：

${\displaystyle f'(3)=108+6\cos(9)-{\frac {e^{3}}{3}}-\ln(3)e^{3}\,}$

如果函数的导数${\displaystyle f'(x)\,}$在${\displaystyle x\,}$处可导，则称${\displaystyle [f'(x)]'\,}$为${\displaystyle x\,}$的二阶导数。记做：${\displaystyle f''(x)\,}$，${\displaystyle y''\,}$，${\displaystyle {\frac {{\rm {d}}^{2}y}{{\rm {d}}x^{2}}}}$或${\displaystyle {\frac {{\rm {d}}^{2}f(x)}{{\rm {d}}x^{2}}}}$^[2]:132、

二阶导数可用于求解函数凹凸性问题。 ${\displaystyle f''(x)>0}$函数在x上凹。 ${\displaystyle f''(x)<0}$函数在x下凹。

二阶导数的导数称为三阶导数，记做${\displaystyle f'''(x)\,}$，${\displaystyle y'''\,}$，${\displaystyle {\frac {{\rm {d}}^{3}y}{{\rm {d}}x^{3}}}}$或${\displaystyle {\frac {{\rm {d}}^{3}f(x)}{{\rm {d}}x^{3}}}}$

三阶导数的导数称为四阶导数，记做${\displaystyle f^{(4)}(x)\,}$，${\displaystyle y^{(4)}\,}$，${\displaystyle {\frac {{\rm {d}}^{4}y}{{\rm {d}}x^{4}}}}$或${\displaystyle {\frac {{\rm {d}}^{4}f(x)}{{\rm {d}}x^{4}}}}$

一般的${\displaystyle f(x)\,}$的${\displaystyle n-1\,}$阶导数的导数称为${\displaystyle f(x)\,}$的${\displaystyle n\,}$阶导数，记为${\displaystyle f^{(n)}(x)\,}$，${\displaystyle y^{(n)}\,}$，${\displaystyle {\frac {{\rm {d}}^{n}y}{{\rm {d}}x^{n}}}}$或${\displaystyle {\frac {{\rm {d}}^{n}f(x)}{{\rm {d}}x^{n}}}}$^[2]:133

一般来说，高阶导数的计算和导数一样，可以按照定义逐步求出。同时，高阶导数也有求导法则：

• ${\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(u\pm v)={\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}u\pm {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}v}$
• ${\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(Cu)=C{\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}u\ }$
• ${\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(u\cdot v)=\sum _{k=0}^{n}C_{k}^{n}{\frac {{\rm {d}}^{n-k}}{{\rm {d}}x^{n-k}}}u{\frac {{\rm {d}}^{k}}{{\rm {d}}x^{k}}}v}$（莱布尼兹公式）^[2]:134

因此，可以利用已知的高阶导数求导法则，通过四则运算, 变量代换等方法，求出${\displaystyle n\ }$阶导数。一些常见的有规律的高阶导数的公式如下^[2]:133：

• ${\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}x^{\alpha }=x^{\alpha -n}\prod _{k=0}^{n-1}(\alpha -k)}$
• ${\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}{\frac {1}{x}}=(-1)^{n}{\frac {n!}{x^{n+1}}}}$
• ${\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\ln x=(-1)^{n-1}{\frac {(n-1)!}{x^{n}}}}$

${\displaystyle \!}$

• ${\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}e^{x}=e^{x}\ }$
• ${\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}a^{x}=a^{x}\cdot \ln ^{n}a}$ ${\displaystyle (a>0)\ }$

${\displaystyle \!}$

• ${\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\sin \left(kx+b\right)=k^{n}\sin \left(kx+b+{\frac {n\pi }{2}}\right)}$
• ${\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\cos \left(kx+b\right)=k^{n}\cos \left(kx+b+{\frac {n\pi }{2}}\right)}$

当函数 ${\displaystyle y}$ 的取值不再是实数，而是一般的${\displaystyle \mathbf {R} ^{n}}$中的向量时，仍然可能对其求导。这时的函数值是：${\displaystyle y=\left(y_{1}(x),y_{2}(x),\cdots ,y_{n}(x)\right)}$。每个 ${\displaystyle y_{i}(x),\;\;1\leqslant i\leqslant n}$ 都是一个实数值的函数。具体的例子如二维或者三维空间里的参数方程。因此，对 ${\displaystyle y=f(x)}$ 求导实际上是对每个分量函数 ${\displaystyle y_{i}(x)}$ 求导。

${\displaystyle \mathbf {y} '(t)=(y'_{1}(t),\cdots ,y'_{n}(t)).}$^[2]:191

这也符合定义

${\displaystyle \mathbf {y} '(t)=\lim _{h\to 0}{\frac {\mathbf {y} (t+h)-\mathbf {y} (t)}{h}},}$

设${\displaystyle \left(e_{1},e_{2},\cdots e_{n}\right)}$为${\displaystyle \mathbf {R} ^{n}}$的一组基，那么对函数：${\displaystyle y\,:t\,\mapsto \,y_{1}(t)e_{1}+y_{2}(t)e_{2}+\cdots y_{n}(t)e_{n},}$

其导函数为：${\displaystyle y'(t)=y'_{1}(t)e_{1}+y'_{2}(t)e_{2}+\cdots y'_{n}(t)e_{n}}$

如果有函数 ${\displaystyle f}$ 其自变量不是单个实数，而是多于一个元素，例如：

${\displaystyle f(x,y)=x^{2}+xy+y^{2}.\,}$

这时可以把其中一个元素（比如 ${\displaystyle x}$ ）看做参数，那么 $$