Стандартизована оцінка — Вікіпедія

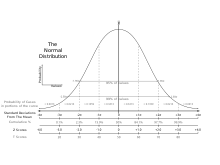
У статистиці стандартна оцінка — це кількість стандартних відхилень, на яку значення необробленої оцінки (тобто спостережуваного значення або точки даних) вище або нижче середнього значення того, що спостерігається або вимірюється. Необроблені бали вище середнього мають позитивні стандартні бали, а ті, що нижче середнього, мають негативні стандартні бали.

Він розраховується шляхом віднімання середнього значення генеральної сукупності від індивідуального необробленого балу, а потім ділення різниці на стандартне відхилення генеральної сукупності. Цей процес перетворення необробленої оцінки в стандартну оцінку називається стандартизацією або нормалізацією (проте «нормалізація» може стосуватися багатьох типів співвідношень; див. Нормалізація для отримання додаткової інформації).

Стандартні бали найчастіше називають z -балами; ці два терміни можуть використовуватися як взаємозамінні, як і в цій статті. Інші еквівалентні терміни, що використовуються, включають z-значення, z-статистику, нормальний бал, стандартизовану змінну та тягу у фізиці високих енергій.^[1]^[2]

Обчислення z-показника вимагає знання середнього значення та стандартного відхилення повної сукупності, до якої належить точка даних; якщо є лише вибірка спостережень із генеральної сукупності, то аналогічне обчислення з використанням вибіркового середнього та вибіркового стандартного відхилення дає t -статистику.

Розрахунок[ред. | ред. код]

Якщо середнє значення сукупності та стандартне відхилення сукупності відомі, необроблений бал x перетворюється на стандартний бал за^[3]

$z={x-\mu \over \sigma }$

де:

μ – середнє значення сукупності,

σ — стандартне відхилення сукупності.

Абсолютне значення z представляє відстань між необробленим показником x і середнім значенням сукупності в одиницях стандартного відхилення. z є негативним, якщо необроблений бал нижче середнього, позитивним, якщо вище.

Обчислення z за цією формулою вимагає використання середнього значення сукупності та стандартного відхилення сукупності, а не середнього значення чи відхилення вибірки. Однак знання справжнього середнього значення та стандартного відхилення сукупності часто є нереалістичним очікуванням, за винятком таких випадків, як стандартизоване тестування, коли вимірюється вся сукупність.

Якщо середнє значення сукупності та стандартне відхилення сукупності невідомі, стандартний бал можна оцінити за допомогою вибіркового середнього значення та стандартного відхилення вибірки як оцінки значень сукупності.^[4]^[5]^[6]^[7]

У цих випадках z -показник визначається як

$z={x-{\bar {x}} \over S}$

де:

{\bar {x}}

є середнім значенням вибірки,

S — стандартне відхилення вибірки.

Хоча це завжди слід зазначати, різниця між використанням генеральної сукупності та вибіркової статистики часто не робиться. У будь-якому випадку чисельник і знаменник рівнянь мають однакові одиниці вимірювання, тому одиниці компенсуються діленням, а z залишається безрозмірною величиною.

Додатки[ред. | ред. код]

Z-тест[ред. | ред. код]

Z-показник часто використовується в z-критерії стандартизованого тестування – аналогі t-критерію Стьюдента для сукупності, параметри якої відомі, а не оцінені. Оскільки знати всю популяцію дуже незвично, t-тест використовується набагато ширше.

Інтервали прогнозування[ред. | ред. код]

Стандартну оцінку можна використовувати для розрахунку інтервалів передбачення. Інтервал передбачення [L, U ], що складається з нижньої кінцевої точки, позначеної L, і верхньої кінцевої точки, позначеної U, — це такий інтервал, що майбутнє спостереження X буде лежати в інтервалі з високою ймовірністю. $\gamma$ , тобто

$P(L<X<U)=\gamma ,$

Для стандартної оцінки Z від X це дає:^[8]

$P\left({\frac {L-\mu }{\sigma }}<Z<{\frac {U-\mu }{\sigma }}\right)=\gamma .$

Визначаючи квантиль z таким чином, що

$P\left(-z<Z<z\right)=\gamma$

це слідує:

$L=\mu -z\sigma ,\ U=\mu +z\sigma$

Контроль процесів[ред. | ред. код]

У додатках керування процесом значення Z забезпечує оцінку ступеня, до якого процес працює не за призначенням.

Порівняння балів, виміряних за різними шкалами: ACT і SAT[ред. | ред. код]

Коли оцінки вимірюються за різними шкалами, їх можна конвертувати в z-показники, щоб полегшити порівняння. Дітц та ін. ^[9] наводять наступний приклад, порівнюючи бали учнів на (старих) тестах SAT і ACT для середньої школи. У таблиці показано середнє значення та стандартне відхилення для загальних балів за SAT та ACT. Припустімо, що студент A набрав 1800 балів на SAT, а студент B набрав 24 бали на ACT. Хто зі студентів показав кращі результати порівняно з іншими учасниками тестування?

	SAT	ДІЙ
Середній	1500	21
Стандартне відхилення	300	5

Z-бал для студента А є

$z={x-\mu \over \sigma }={1800-1500 \over 300}=1$

Z-бал для студента Б становить

$z={x-\mu \over \sigma }={24-21 \over 5}=0.6$

Оскільки студент A має вищий z-бал, ніж студент B, студент A показав кращі результати порівняно з іншими тестувальниками, ніж студент B.

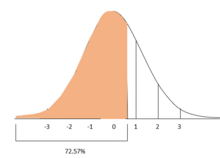
Відсоток спостережень нижче z-показника[ред. | ред. код]

Продовжуючи приклад балів ACT і SAT, якщо додатково можна припустити, що обидва бали ACT і SAT розподілені нормально (що є приблизно правильним), тоді z-бали можна використовувати для розрахунку відсотка учасників тестування, які отримали нижчі бали, ніж студенти А і Б.

Кластерний аналіз і багатовимірне масштабування[ред. | ред. код]

«Для деяких багатовимірних методів, таких як багатовимірне масштабування та кластерний аналіз, концепція відстані між одиницями в даних часто становить значний інтерес і важливе значення... Коли змінні в багатовимірному наборі даних мають різні масштаби, має сенс розрахувати відстані після певної форми стандартизації».^[10]

Аналіз головних компонент[ред. | ред. код]

В аналізі головних компонентів «змінні, виміряні на різних шкалах або на загальній шкалі з дуже різними діапазонами, часто стандартизовані».^[11]

Відносна важливість змінних у множинній регресії: стандартизовані коефіцієнти регресії[ред. | ред. код]

Стандартизація змінних перед множинним регресійним аналізом іноді використовується як допомога для інтерпретації.^[12] (сторінка 95) зазначте наступне.

«Стандартизований нахил регресії — це нахил у рівнянні регресії, якщо X і Y стандартизовані… Стандартизація X і Y здійснюється шляхом віднімання відповідних середніх значень із кожного набору спостережень і ділення на відповідні стандартні відхилення… У множинній регресії, де кілька Використовуються змінні X, стандартизовані коефіцієнти регресії кількісно визначають відносний внесок кожної змінної X».

Однак Kutner et al.^[13] (стор. 278) дають таке застереження: «… треба бути обережним щодо інтерпретації будь-яких коефіцієнтів регресії, незалежно від того, стандартизовані вони чи ні. Причина полягає в тому, що коли змінні предиктора корелюють між собою, … коефіцієнти регресії залежать від інші змінні предикторів у моделі... На величини стандартизованих коефіцієнтів регресії впливає не лише наявність кореляцій між змінними предикторів, але й інтервали спостережень за кожною з цих змінних. Іноді ці інтервали можуть бути досить довільними. Отже,, як правило, нерозумно інтерпретувати величини стандартизованих коефіцієнтів регресії як відображення порівняльної важливості змінних предикторів».

Стандартизація в математичній статистиці[ред. | ред. код]

У математичній статистиці випадкова величина X стандартизується шляхом віднімання її очікуваного значення $\operatorname {E} [X]$ і ділення різниці на її стандартне відхилення $\sigma (X)={\sqrt {\operatorname {Var} (X)}}:$

$Z={X-\operatorname {E} [X] \over \sigma (X)}$

Якщо випадкова змінна, що розглядається, є вибірковим середнім для випадкової вибірки $\ X_{1},\dots ,X_{n}$ з X:

${\bar {X}}={1 \over n}\sum _{i=1}^{n}X_{i}$

то стандартизована версія

Z={\frac {{\bar {X}}-\operatorname {E} [{\bar {X}}]}{\sigma (X)/{\sqrt {n}}}}

Де дисперсія стандартизованого вибіркового середнього розраховувалась наступним чином:

{\begin{array}{l}\operatorname {Var} \left(\sum x_{i}\right)=\sum \operatorname {Var} (x_{i})=n\operatorname {Var} (x_{i})=n\sigma ^{2}\\\operatorname {Var} ({\overline {X}})=\operatorname {Var} \left({\frac {\sum x_{i}}{n}}\right)={\frac {1}{n^{2}}}\operatorname {Var} \left(\sum x_{i}\right)={\frac {n\sigma ^{2}}{n^{2}}}={\frac {\sigma ^{2}}{n}}\end{array}}

Т-оцінка[ред. | ред. код]

В освітньому оцінюванні Т-бал є стандартним балом Z, зміщеним і масштабованим, щоб мати середнє значення 50 і стандартне відхилення 10.^[14]^[15]^[16] Він також відомий як хенсачі японською мовою, де ця концепція набагато ширше відома та використовується в контексті вступу до середньої школи та університету.

При вимірюванні щільності кісткової тканини T-показник є стандартним показником вимірювання порівняно з популяцією здорових 30-річних дорослих, і має звичайне середнє значення 0 і стандартне відхилення 1.^[17]

Див. також[ред. | ред. код]

Примітки[ред. | ред. код]

↑ Mulders, Martijn, ред. (2017). 2015 European School of High-Energy Physics: Bansko, Bulgaria 02 - 15 Sep 2015. CERN Yellow Reports: School Proceedings. Geneva: CERN. ISBN 978-92-9083-472-4.
↑ Gross, Eilam (6 листопада 2017). Practical Statistics for High Energy Physics. CERN Yellow Reports: School Proceedings (англ.). 4/2017: 165—186. doi:10.23730/CYRSP-2017-004.165.
↑ E. Kreyszig (1979). Advanced Engineering Mathematics (вид. Fourth). Wiley. с. 880, eq. 5. ISBN 0-471-02140-7.
↑ Spiegel, Murray R.; Stephens, Larry J (2008), Schaum's Outlines Statistics (вид. Fourth), McGraw Hill, ISBN 978-0-07-148584-5
↑ Mendenhall, William; Sincich, Terry (2007), Statistics for Engineering and the Sciences (вид. Fifth), Pearson / Prentice Hall, ISBN 978-0131877061
↑ Glantz, Stanton A.; Slinker, Bryan K.; Neilands, Torsten B. (2016), Primer of Applied Regression & Analysis of Variance (вид. Third), McGraw Hill, ISBN 978-0071824118
↑ Aho, Ken A. (2014), Foundational and Applied Statistics for Biologists (вид. First), Chapman & Hall / CRC Press, ISBN 978-1439873380
↑ E. Kreyszig (1979). Advanced Engineering Mathematics (вид. Fourth). Wiley. с. 880, eq. 6. ISBN 0-471-02140-7.
↑ Diez, David; Barr, Christopher; Çetinkaya-Rundel, Mine (2012), OpenIntro Statistics (вид. Second), openintro.org
↑ Everitt, Brian; Hothorn, Torsten J (2011), An Introduction to Applied Multivariate Analysis with R, Springer, ISBN 978-1441996497
↑ Johnson, Richard; Wichern, Wichern (2007), Applied Multivariate Statistical Analysis, Pearson / Prentice Hall
↑ Afifi, Abdelmonem; May, Susanne K.; Clark, Virginia A. (2012), Practical Multivariate Analysis (вид. Fifth), Chapman & Hall/CRC, ISBN 978-1439816806
↑ Kutner, Michael; Nachtsheim, Christopher; Neter, John (204), Applied Linear Regression Models (вид. Fourth), McGraw Hill, ISBN 978-0073014661
↑ John Salvia; James Ysseldyke; Sara Witmer (29 January 2009). Assessment: In Special and Inclusive Education. Cengage Learning. с. 43–. ISBN 978-0-547-13437-6.
↑ Edward S. Neukrug; R. Charles Fawcett (1 January 2014). Essentials of Testing and Assessment: A Practical Guide for Counselors, Social Workers, and Psychologists. Cengage Learning. с. 133–. ISBN 978-1-305-16183-2.
↑ Randy W. Kamphaus (16 August 2005). Clinical Assessment of Child and Adolescent Intelligence. Springer. с. 123–. ISBN 978-0-387-26299-4.
↑ Bone Mass Measurement: What the Numbers Mean. NIH Osteoporosis and Related Bone Diseases National Resource Center. National Institute of Health. Процитовано 5 August 2017.

Посилання[ред. | ред. код]

Інтерактивний Flash про z-показники та ймовірності нормальної кривої від Джима Ріда

[1] Mulders, Martijn, ред. (2017). 2015 European School of High-Energy Physics: Bansko, Bulgaria 02 - 15 Sep 2015. CERN Yellow Reports: School Proceedings. Geneva: CERN. ISBN 978-92-9083-472-4.

[2] Gross, Eilam (6 листопада 2017). Practical Statistics for High Energy Physics. CERN Yellow Reports: School Proceedings (англ.). 4/2017: 165—186. doi:10.23730/CYRSP-2017-004.165.

[3] E. Kreyszig (1979). Advanced Engineering Mathematics (вид. Fourth). Wiley. с. 880, eq. 5. ISBN 0-471-02140-7.

[SpiegelStephens2008-4] Spiegel, Murray R.; Stephens, Larry J (2008), Schaum's Outlines Statistics (вид. Fourth), McGraw Hill, ISBN 978-0-07-148584-5

[Mendenhall2007-5] Mendenhall, William; Sincich, Terry (2007), Statistics for Engineering and the Sciences (вид. Fifth), Pearson / Prentice Hall, ISBN 978-0131877061

[GlantzSlinker2016-6] Glantz, Stanton A.; Slinker, Bryan K.; Neilands, Torsten B. (2016), Primer of Applied Regression & Analysis of Variance (вид. Third), McGraw Hill, ISBN 978-0071824118

[Aho2014-7] Aho, Ken A. (2014), Foundational and Applied Statistics for Biologists (вид. First), Chapman & Hall / CRC Press, ISBN 978-1439873380

[8] E. Kreyszig (1979). Advanced Engineering Mathematics (вид. Fourth). Wiley. с. 880, eq. 6. ISBN 0-471-02140-7.

[Diez2012-9] Diez, David; Barr, Christopher; Çetinkaya-Rundel, Mine (2012), OpenIntro Statistics (вид. Second), openintro.org

[EverittHothorn2011-10] Everitt, Brian; Hothorn, Torsten J (2011), An Introduction to Applied Multivariate Analysis with R, Springer, ISBN 978-1441996497

[JohnsonWichern2007-11] Johnson, Richard; Wichern, Wichern (2007), Applied Multivariate Statistical Analysis, Pearson / Prentice Hall

[AfifiMayClark2012-12] Afifi, Abdelmonem; May, Susanne K.; Clark, Virginia A. (2012), Practical Multivariate Analysis (вид. Fifth), Chapman & Hall/CRC, ISBN 978-1439816806

[KutnerNachtsheim2004-13] Kutner, Michael; Nachtsheim, Christopher; Neter, John (204), Applied Linear Regression Models (вид. Fourth), McGraw Hill, ISBN 978-0073014661

[14] John Salvia; James Ysseldyke; Sara Witmer (29 January 2009). Assessment: In Special and Inclusive Education. Cengage Learning. с. 43–. ISBN 978-0-547-13437-6.

[15] Edward S. Neukrug; R. Charles Fawcett (1 January 2014). Essentials of Testing and Assessment: A Practical Guide for Counselors, Social Workers, and Psychologists. Cengage Learning. с. 133–. ISBN 978-1-305-16183-2.

[16] Randy W. Kamphaus (16 August 2005). Clinical Assessment of Child and Adolescent Intelligence. Springer. с. 123–. ISBN 978-0-387-26299-4.

[17] Bone Mass Measurement: What the Numbers Mean. NIH Osteoporosis and Related Bone Diseases National Resource Center. National Institute of Health. Процитовано 5 August 2017.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]